Part I
1. Temporal Perspective as an Empirical Necessity
2. Relativity of Simultaneity
3. Relativistic Interdependence of Specifying Place and Time
4. Spacelike and Timelike Intervals
5. The Locality of the Present
6. No Existential Ambiguity in Special Relativity
7. Minkowski Diagrams and Their Misuse
Notes to Part I
Part II
8. McTaggart’s Argument against the Reality of Time
9. Reality of Time Distinguished from Discourse about Time
10. Gale’s Criticism of McTaggart: A-Theory and B-Theory
11. Philosophy of Temporal Series Applied to Special Relativity
12. Extension to General Relativity
Notes to Part II
Physics, whether considered as an empirical, quantitative science or as a philosophy of nature, deals in the first place with changes in the sensible world. The order of succession of various observed states is defined by what we call the order of time. The instant an observation is made, or rather experienced, we call the present, while all observations already known at present are defined to have occurred in the past, in the order in which we experience them. What we call the future consists of presently unknown observations that will follow the present just as the present follows the past. We can only know these future observations when they are no longer future and become present. The contents of observations, for the physicist, measure states of the sensible world. As measurements of the same object vary in content from one moment to the next, we infer that the object is changing in some property over time. This inference entails assuming that each physical state of the object is nearly simultaneous with the corresponding moment of observation, or at least that the signal from each successive state takes the same duration of time to reach us, so that the temporal succession of our observations is an image of the temporal succession of physical states.
We can see from the outset that past, present and future, even in a classical paradigm, are always defined with respect to a point of observation or experience, i.e., a perspective. Questions such as when is the present?
or indeed any temporal question can only be answered after a perspective has been chosen. All existential propositions, insofar as they pertain to things that exist in time, coming into being and passing away, depend for their answer on a perspective-dependent definition of the present.
The answer to the question Is Socrates alive?
depends on whether it is asked in 405 BC or AD 2018. The ‘is’ is understood to refer to the temporal present, since Socrates is a being that exists in time. By contrast, if we ask, Does a triangle have three sides?
no specification of temporal perspective is needed, since we are regarding triangles and their properties as formal relations abstracted from time.
Physics generally deals with the first kind of statement when addressing questions of physical fact and the latter kind when dealing with physical laws or constants. Physical facts occur in temporal succession, so we must specify a value (relative or absolute) for our time variable in order to define whether something has occurred, and to calculate what will occur in the future. Yet there is also a relational structure in nature defined by physical laws that have the same form for all time. These laws, as well as certain fundamental constants and invariants, may be regarded atemporally. Even here we must be cautious, as it may turn out that many such laws or constants hold only for certain periods in the history of our universe. After all, physical laws are validated by observations, so they need not be applicable to any scope broader than the range of observations in which they were established. The laws of Newtonian mechanics are true, but only in a limited domain. The same may turn out to be the case for laws and constants we currently regard as universal and eternal.
It is clear, then, that defining a temporal perspective is important not only for establishing whether physical facts are occurrent, but also for defining whether certain physical laws are even applicable. Further, without a well-defined order of temporal succession, we would not know how to apply the laws of physics in the correct order, yielding the correct result. This is especially true in quantum mechanics, where operators representing observables do not commute, so the order in which you apply them (each application representing a measurement) alters the probabilities of results.
In a classic thought experiment, Einstein showed that it is impossible to produce a single definition of simultaneity for distant events. Even observers at the same place and time will disagree on the computed temporal priority of distant events. This involves no existential paradox, as we shall see upon closer examination.
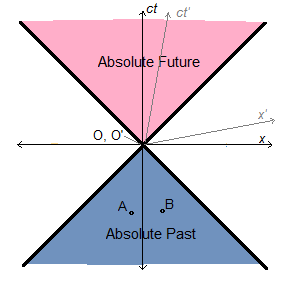
Two light signals or flashes originating at points A and B on the ground reach a ground observer O at the exact same time that a passenger on a train moving in the direction from A to B at some velocity v passes the ground observer at the same point O. [Figure 1] We denote the train observer’s position as O′ to remind us that his frame of reference is different from that of the ground observer. Both light signals reach both observers simultaneously. They never disagree about the order in which signals reach them; i.e., the order in which events appear to them. Rather, they may disagree on the computed or indirectly inferred times in the past when the original events supposedly occurred.
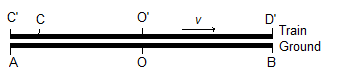
If we assume A and B to be equidistant from O in the rest frame of the ground, the ground observer will figure that both flashes must have originated at the same time
in his frame. If he defines the time of observation to be t = 0, then the computed time of origin will be t = -l/c for both flashes, where l is the length of AO or BO, and c is the perceived speed of light. The minus sign indicates that the times of origin are in the past with respect to the time of observation.
The train observer may measure the distance in the train’s frame with the help of assistants at points C′ and D′ on the train, who happen to have been passing the points A and B at the instants their respective flashes originated. He would therefore think the distance traveled is O′C′ for the rear flash and O′D′ for the front flash. From the perspective of the ground observer, these lengths are not the same as OB and OA. By the time the rear flash reaches the observer at O′, C′ will have moved over to the right some distance with respect to the ground, but since observations in the train’s frame do not take into account motion with respect to the ground, the distance perceived by the train observer will be some quantity shorter than AO, according to the ground observer. Likewise, the ground observer will think the train observer overestimates the distance traveled by the front flash, giving a quantity longer than OB.
Classically, this would lead to no paradox, since the train observer ought to also perceive the rear light signal from A to be moving more slowly, at a speed c - v (since the train is moving away from its source) and the front signal from B to be moving faster, at a speed c + v. This offsets the perceived difference in signal path lengths, so the train observer agrees with the ground as to the simultaneous origin of both signals.
Once we accept, however, the strange fact that the speed of light is perceived to be the same in every inertial frame, no such offset and no such agreement is possible. The disagreement in path length results in a disagreement about how far in the past each signal originated. Both observers receive both signals at the same time, but they make different inferences about when they originated (and how far away). The one in the rest frame where the sources are equidistant (on the ground in this example) will compute that they are simultaneous in origin, while the other will think not.
A casual inspection of the train example might lead one to believe that the perceived difference in path distance is simply vt, where v is the velocity of the train with respect to the ground and t is the time c/l taken for light to traverse the length l of AO. Yet the relativity of simultaneity implies that we cannot naively assume that t and l have the same units in both reference frames. It is one thing to measure an object when our ruler is at rest with respect to the object measured, but another when the measured object is in motion with respect to the observer. In the latter case, we must define, using some frame-specific convention of simultaneity, that we are measuring both ends of the object at the same time. Accordingly, we must also multiply by the Lorentz factor γ to yield the correct transformation of space and time coordinates between observers:
x′ = γ(x - vt)
t′ = γ(t - vx/c2)
The different units of measurement used in each reference frame are due to the fact that different observers judge different events to be simultaneous. In short, relativity of simultaneity and the frame-dependence of length and time measurements (Lorentz contraction and time dilation) are all of a cloth. (See discussion in Basic Issues in Natural Philosophy, IV or any standard physics text.)
None of this involves any contradiction about the reality of past, present and future. For both observers, the origins of both flashes already occurred in the past. Both observers perceive both light signals simultaneously. They only disagree on the inferred relative priority of the origins of these signals.
We can get the same relativity of simultaneity for future events. If the observer at O should instead send light signals outward to A and B, he and the observer at O′ will disagree on the inferred priority of arrival at each endpoint. The ground observer calculates that the signals will reach A and B simultaneously, while the train observer calculates that a flash will reach A before a flash reaches B. Still, there is no ambiguity about observed temporal succession, insofar as both observers agree that the signals left at the same time, and that both arrivals will occur in the future.
Naturally, we could reverse the computed order of priority by considering an observer on a train moving in the opposite direction. Thus, among three different observers, the event EA when the flash is emitted (or received) at A could be prior to the event EB at B, or the reverse, or they could be simultaneous.
There is no single right answer to the question of simultaneity or priority for the origins (or arrivals) of signals at A and B, but this yields no ontological paradoxes. Though it would be a contradiction for the event EA to be in the past of EB and EB to be in the past of EA, in fact neither event can be in the physical past or future of the other, since no signal or effect can reach either event. We must here make clear that an event Ei is distinct from a mere spatial position (A or B), because an event also specifies time. Certainly it is possible to send a light signal from A to B. But it is impossible to send any signal from the place and time EA of the rear signal‘s origin that would arrive at the place and time EB of the front signal’s origin. This is obvious from the assumed fact that actual light signals originating from EA and EB reach O simultaneously, having traversed only half the distance AB. By the time they traverse the other half, they will arrive at points in the future of EA and EB. Thus neither event can be in the physical past or future of the other; i.e., no effect, signal, or any other trace of either event can reach the other, not even in principle.
Observers at the same place and time, yet in relative motion to each other, will always agree about which observed events have already happened. They agree on which signals they are receiving now, and likewise agree that such signals are the traces or effects of some past event. The set of all events that might, at least in principle, produce signals or effects that reach the present constitute what we have called the physical past, and is more conventionally called the absolute past,
signifying that this is independent of reference frame. The absolute
past, nonetheless, is still defined relative to the perspective we define to be the present,
as was the case even classically.
Observers at the same place and time in different reference frames (i.e., moving at different velocity) will disagree only on the inferred priority or simultaneity between what are called spatially separated
events. This term does not simply mean events that occur at different points in space, but is more restrictive. They are events between which no direct signaling is possible, even in principle, since no signal can travel faster than the speed of light. This is not a speed limit
in the sense of some qualitative limitation of matter, but a reflection of the geometric structure of spacetime. It is not that matter could travel faster than light if only it were given some extra impetus, for that supposes there is some absolute space that could be defined independently of the actual motions of signals. Superphotonic signaling would make special relativity self-contradictory. Relativity forces us from the outset to accept that all space and time measurements are definable only in terms of photonic or subphotonic signal propagation.
Spatially separated events cannot be in the absolute past or future of each other in any frame of reference. That is to say, there can be no timeline or history of a given physical object, typically called a world line
in which both these events occur. It is possible, in general, for a single observer to receive signals or effects of both events at some point in their overlapping absolute futures. There is no scenario, however, where our choice of priority or simultaneity for such events yields any ontological paradoxes about whether or not an event has already occurred. Any two observers present at the same place and time will always agree on which events have already occurred, even if the observers are in different reference frames (i.e., they have non-zero relative velocity).
It may be noted that observers at the spatially separated events EA and EB themselves will, in general, disagree on which events have already occurred. Does this not create a paradox, where the reality of events in the immediate past of EB depends on resolving its simultaneity or priority with respect to EA? Not at all, for we have no basis for determining that the spatially separated observers are making their observations simultaneously. Thus there is no basis for regarding their differing views as entailing a contradiction. After all, there is no contradiction in two observers disagreeing on whether Socrates has already died if we cannot know that the observations are made at the same time.
Einstein’s theory of relativity imposes a new constraint on defining a temporal perspective. In classical mechanics, it was assumed that when you defined the present
(or any other value of the time variable) at a certain place, the same temporal value held for all other places. This meant that you could define the present
(or any other time) universally, independent of spatial location. Under special relativity, however, this assumption breaks down, as definitions of simultaneity across space depend on reference frame (relative velocity). In order to define the present
universally, one must specify a choice of reference frame from which observations are made. This is not purely formalistic, as the reference frame is defined by the actual state of motion of the observer.[1] Further, within that frame, one must choose a convention for the one-way speed of light signals in each direction, and that convention allows you to construct a definition of simultaneity for all points in space. We should emphasize, however, that such construction is made from the perspective of an observer sending and receiving light signals to and from distant places. Such constructions of simultaneity are formalistic, and do not enable an observer to see everything at once.
Indeed, there is no univocal definition of everything at once.
From the temporal sequence of events we can observe, we construct sequences for those we cannot observe even in principle.
The non-universality of the present implies that, to define the present, we must specify not only when,
but where.
Defining the present
on Earth need not tell us anything about what is the present on Alpha Centauri. This relativity of simultaneity only obtains between spatially separated events. It does not abolish or render ambiguous the temporal succession of observable events, i.e., those connected by timelike intervals (of signals communicating what we observe). These are also the only events that can be related causally. If temporal succession were not physically real, it is bizarre that this constraint should exist. After all, if past, present and future are truly of no physical consequence, then there is nothing to prevent any event from affecting events in its past.
Although certain interpretations of quantum mechanics make such claims of reverse causality, this is not the case in relativity per se, so we cannot invoke relativity in defense of such interpretations. Further, even in quantum mechanics, you cannot have a measurement outcome affect a past measurement outcome. The supposed reverse causation is in a retroactive change in potentiality (of the wavefunction or operator, depending on which picture is used), not in actual outcomes, which would be absurd. Once something is done in the past, it cannot be undone as past.
To answer, Is Socrates alive?
I must specify time and place. The answer is unambiguously no
on Earth in 2018, but there may not be an unambiguous answer at time points in distant galaxies. Still, anyone who knows the death of Socrates is in an unambiguous future of that event.
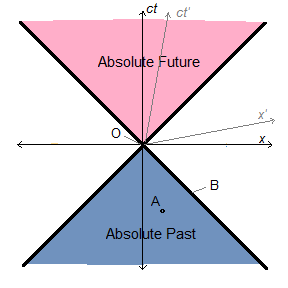
Any event whose trace can reach Earth in 2018 by light or sub-light signal is in Earth-2018’s absolute past, regardless of the reference frame (relative velocity) of an observer on Earth in 2018. The invariance of the speed of light guarantees that the light cone
of a present-day Earth observer will have the same boundary in any reference frame. Naturally, this absolute past
is still perspective-dependent (as was the case classically), since it is defined with respect to the present on Earth
rather than some other time and place. Still, the various local definitions of the here-and-now present are all compatible, as proved by the fact that spatially distant world lines can converge in each other’s light cones and not have any causal or temporal paradoxes where the future precedes the past, or an effect precedes its cause. When two space travelers meet, they will surely agree that their meeting point is the present,
however much their past perceptions of time may have diverged. It will never be the case that one traveler cannot see the other because the other is in his future,
due to some non-synchronicity of converging world lines. In fact, we may consider a world line to be simply a graph of the successive presents
for a given object.
Under special relativity, we may define a pseudometric distance
between any two events. This distance
can be defined empirically by the spatial distance and temporal duration between the two events, on the assumption of the invariance of light speed. From the relativistic phenomena of Lorentz contraction and time dilation, we know that the perceived path length and time duration between events depends on the observer’s reference frame. Yet the perceived time dilates by the same Lorentz factor by which perceived length contracts, so we have a frame-invariant quantity, the pseudometric distance squared: s2 = x2 + y2 + z2 - c2t2.
There is nothing magical about s2 being invariant. It is a consequence of the requirement that the speed of light is invariant for a light wave propagating in any direction. After some time t, it travels to some point (x, y, z), so c2t2 = x2 + y2 + z2. The set of all possible endpoints for propagation in any direction is defined by the equation: c2t2 - x2 - y2 - z2 = 0. If a wavefront is propagating spherically in all directions, then the invariance of light speed implies that a similar equation must hold for the locus in all other frames: c2t′ 2 - x′ 2 - y′ 2 - z′ 2 = 0. It can be shown mathematically that only reflections, spatial rotations, and the Lorentz transformation (for translations of relative velocity) leave this quantity the same. Basically, the invariance of s2 is another way of stating the requirement that the speed of light is the same in all reference frames, for light traveling in any direction.
The pseudo-distance s becomes visualizable in Minkowski diagrams, which plot space and time as though they were different spatial dimensions. This geometric convenience should never be confused with physical reality, however, as is clear from the fact that the distance-squared takes negative values, contrary to the positive values implied by pictorial representation. Minkowski himself preferred to denote the time axis with imaginary values ict, thereby containing the negative contribution to distance in the variable and making the geometric positive-definite presentation justifiable. Whether we use ict or ct, Minkowski diagrams offer a convenient way to visualize or compute the transformation of space and time coordinates from one frame to another. (For further discussion, see Basic Issues in Natural Philosophy, IV or a standard physics textbook.)
In particular, the use of diagrams with the s2 pseudometric encourages us to think in terms of spacetime intervals, though such intervals are not, in general, directly measured. These intervals are characterized as spacelike or timelike depending on whether they fall inside or outside the light cone
defined by possible trajectories of light from the origin.
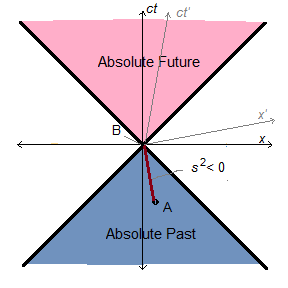
In cases where one event A can be observed by someone at another event B, A is certainly in the past of B. (N.B.: Henceforth we use capital letters such as A, B, O to denote events, not mere spatial points.) Since no signal can travel faster than light, the pseudometric distance-squared s2 must be less than zero. This allowance of negative values should make it clear that s does not measure any real extension; indeed it fails to meet even the most generic mathematical criteria for a distance function. Nonetheless, it is conventional to speak equivocally of such pairs of events as connected by a timelike interval,
though there is no metric where a distance can be less than zero.
Recall that we are effectively cheating in our Minkowski diagrams, representing the ct axis as though time made a positive contribution to distance.
Minkowski himself, more coherently, made the temporal axis imaginary-valued, i.e., ict, since the square of this will give a negative contribution. Either way, it is clear that space and time are categorically dissimilar, notwithstanding the interdependence of the magnitudes of their measurements.
It is invalid to treat spacetime as a four-dimensional extension, with events constituting parts of some substance, since the notion of material extension presupposes additivity, so that parts combine to form a greater whole. Yet the timelike dimension, with its negative distance, actually makes a negative contribution to pseudometric area or volume. Temporal duration, far from being another extension analogous to space, is something that is antithetical to spatial extension. If the spatial distance between two events seems longer compared to another frame, the duration between them will seem smaller, and vice versa. Space and time are related to each other in offset or counterbalance when measuring a motion, not as parts of a whole.
A timelike interval remains timelike in any inertial frame of reference, since the value of s2 is frame-invariant. Such timelike separated
events admit of direct observation; i.e., an observer at B can receive a signal from A. Note that A is in the past of B regardless of reference frame. There is no ambiguity whatsoever in the order of temporal succesion, though the duration of time depends on choice of frame.
Signals traveling at light speed have a pseudometric distance of zero, so the events of sending and receiving such signals are said to be connected by a null interval.
We may interpret the null distance as indicating that the speed of light is a limit, holding the place that infinite speed held in classical mechanics. The invariance of s2 implies that a null interval remains such in every inertial frame, which is just another way of indicating the postulate of the invariance of light speed. The boundaries of a light cone are null intervals, so the definition of a light cone with respect to an event at the origin is frame-invariant.
What about intervals between one event and another outside its light cone? Surely, events outside the light cone may exist, but can we say anything about when they occur? As mentioned previously, any attempt to define a chronology depends on construction of a convention for simultaneity in a given frame, and this is done by sending light signals. We cannot get around the inherent impossibility of superphotonic travel by this formalistic construction of simultaneity. So-called spacelike intervals
are merely constructed or inferred for events, never observed or traversed in physical reality. They are called spacelike
because the pseudo-distance is positive, as we should expect for a spatial distance.
Relativity of simultaneity exists only between events connected by a spacelike interval, which is to say, only between events that are outside each other’s light cone, so that they cannot be causally or physically connected even in principle. Neither is in the past or future of the other. Why, then, should we even attempt to construct a relative chronology for them? It is only a chronology that we infer from the convention of simultaneity we have defined among events whose signals we can observe at the present.
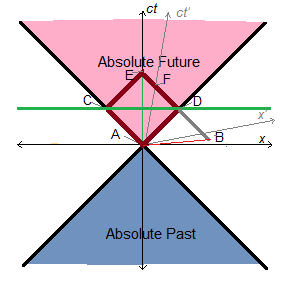
An observer O may receive signals from events A and B in its absolute past, where A and B are spacelike separated from each other. [Figure 5] Another observer O′, in another reference frame moving at some velocity v with respect to that of O, may likewise receive signals from the same two events. Both O and O′ agree that A and B are in their past, but they may disagree on whether A occurred before B. Note that this entails no ontological ambiguity, since A and B have already occurred and are fully actual to both observers. Nor is there any ambiguity in the temporal sequence of any series of events that can be causally related to each other even in principle.
One might ask if the ontological status of B is a matter of ambiguity to observers at A, depending on their reference frame (i.e., relative velocity at A). Yet it would never even occur to observers at A to ask anything about B, which is invisible to them, being outside their absolute past. At best, they may make conjectures about whether something like B will happen in the contingent future, based on observations of events that are in the absolute past of both A and B. Again, no ontological ambiguity is entailed.
Surely, one might insist, there must simultaneously be an observer for whom A is actual and B has not yet happened, and another for whom the reverse is true. In fact, this can never be the case, at least as far as anything physically observable is concerned. Figure 6 shows a putative example of such a scenario. A is in the absolute past of P but not of Q, and B is in the absolute past of Q but not of P. The problem is that we are not justified in making observers at P and Q to be simultaneously observing the spacelike separated events. The same principle of relativity of simultaneity eliminates any scenario where there could be simultaneous disagreement about the ontological status of any event.
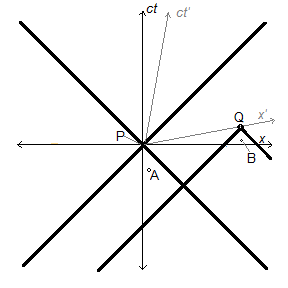
We could choose a particular reference frame x′, ct′, in which P′ and Q′ are formally defined to be simultaneous. Then we might say that there is a contradiction, because an observer in the x, ct frame at P sees A to have occurred while B has not yet happened, yet the observer in the x′, ct′ frame at Q′ sees B to have occurred, yet considers its present to be simultaneous with P. Is this not a contradiction in the ontological status of B? Only if we regard the judgment of simultaneity between P and Q to be objective, but this is contradicted by the principle of relativity of simultaneity. If we were to regard the simultaneity of P and Q as absolute, then we should have to regard x′, ct′ as a privileged frame, and to be consistent we would disregard the judgment in the x, ct frame that B is later than A.
The aforementioned lack of ontological ambiguity or paradox regarding the reality of past, present and future relies on the notion that the present can only be defined locally, so there is no way to univocally coordinate the time perceptions of distant observers. The relativistic idea that the present is not a now
abstracted from space, but also here,
merely articulates what has always been true, though it has been negligible when signal speeds can be considered practically infinite. We can only know the past as it reaches us here and becomes present. Faulkner’s dictum, The past is never dead. It’s not even past,
actually holds some literal truth.
What do we really know of the past and present? Is Socrates alive? Even if he were standing in front of me, the most I can say is, He was alive at some point in my very recent past.
Present
really does mean present now and here. All that is present to me of the outside world are its effects and signals as they reach me. As these effects swiftly reach me in my present, I can safely infer that their causes existed in the recent past. For most terrestrial purposes, light signals are practically instantaneous, so I can treat things I see as simultaneous in time, since the signal time is negligible compared to any biological reaction time, or the speed of ordinary machines, or my psychological experience of the ever-changing present, as an act of self-awareness or other thought requires some duration. Yet even in this ordinary environment, there is in fact some delay between the past object and my present observation. All we really observe is the past made present (here and now) to us by signals or effects.
Every other person or object has a similar experience, being affected only by signals or effects from events in its absolute past, acting only in its present (here and now) and proceeding in time. For every object, time only goes forward, effects never precede their causes, and only the past is observed. There is no ambiguity about what is the absolute past of an event, hence there is no ambiguity of ontological status for any observable events, since all such events are necessarily in the past.
What shall I say of another observer at some other place? I say to that person: You can exist for me only if you are in the same place as me, or, if you are some distance away, only if you are in my immediate or remote past. I do not experience you with absolute immediacy, but only after some lapse of time, when the sound from your voice or light reflected from your face reaches me. For terrestrial purposes, this lapse of time is usually negligible, and we just say everything and everyone around us exists at once in the present,
even though the present
is constantly changing for each of us.
This does not result in any existential contradiction, since you certainly existed at the time you spoke and I certainly exist at the time I hear your voice. What I cannot hold as absolutely certain is what has happened to you in the meantime, between when you spoke and when I hear you. If we were astronomically distant, you could send me regular radio signals from your star system X letting me know you were alive at the time of transmission, and another person from another remote star system Y might do likewise. Yet my perception of which set of signals ended first (i.e., who died first) would depend on my relative velocity (i.e. reference frame) with respect to the other star systems.
Now, if you want to ask who really died first, this is unanswerable if the two deaths are spatially separated events. This ambiguity has no physical implications, because there is no frame of reference in which the death of one person could have been communicated to the place/time of the other person’s death. By the time a signal from system X reaches system Y or vice versa, the deaths of both persons will be in the past of whoever receives the signal. So there is never any physical action that has ontologically ambiguous status. The only limitation is that not everyone can know the ontological status of everything, insofar as not every event can, even in principle, be affected by all other events.
Even in a classical paradigm, the ontological status of events has depended on where a person is situated in time. For my present, the past has already been made actual, though it is known to me now only by the effects or signals that reach my present. With respect to my present, future events are known only contingently; they are not actual. Relativity changes the picture only in requiring that the perspective we call present
must specify a location as well as a time. I can only know as actual what can reach me here in my now.
It is tempting to hold that the perspective-dependence of past, present, and future implies their unreality, but this is to take a position that is the direct negation of the central insight of relativity. Newtonian (and Cartesian) mechanics treated space and time as absolutes that could exist in themselves, abstracted from any observation or measurement. Einstein’s treatment of length and time, by contrast, in all of his famous gedanken experiments, supposes that the notions of length and time have no physical meaning apart from what can be observed in a physical measurement.[2] If a consequence of relativity is that the present can only be defined from a local perspective, it does not follow that the present (or its respective past or future) is unreal. On the contrary, observational, perspective-dependent reality is the only kind of reality that deserves to be called physical, if physics is taken to be an empirical science.
It is true that Einstein himself, as well as Eddington and other physicists and philosophers, often took the relativity of simultaneity as implying a sort of lesser reality or even unreality to the succession of past, present and future. This was not done consistently, however, nor indeed is it possible to apply such a notion consistently, since special relativity offers no frame-independent
or perspective-independent
account of spatiotemporal reality. We can only define the magnitudes of length and duration as perceived in a chosen frame, just as we can only define past, present and future from the perspective of the event of an observation. The only frame-independent
structure is in the transformation between reference frames, but this only gives us information about the relationship between frames, not an absolute set of values for spatial length and temporal duration. Likewise, the only perspective-independent
structure is in the order of temporal succession for timelike-connected events. If A is in the absolute past of B and B is the absolute past of C, then A must be in the absolute past of C. Yet we can not say simply and absolutely what is past
without first choosing a time-place to call present.
There could only be a spatially universal definition of now
if there were a true
reference frame and convention of simultaneity. In fact, every inertial frame can be used to establish a spatially universal definition of simultaneity. The problem is that there is no physical basis for preferring one definition over another, and these do not agree with each other. To define an absolute universal now,
you need two things: first, a choice of frame (i.e., defining absolute rest); second, a synchronization convention. The Einstein convention is to assume that the one-way speed of a light signal is the same in both directions, so that each leg of the round trip takes the same amount of time. So if you send a signal back and forth to another star, you assume that it reached the star in half the time it takes between when you sent it and received the reply. This is just a convention, however, as Einstein and Poincaré realized. There is no way to prove empirically that this is correct, and you could use other conventions to get equally self-consistent synchronization schemes.
If there is an absolute or privileged reference frame, there is no physical way to identify it, due to the invariance of the laws of physics under inertial transformations. We leave it to metaphysicians to decide if such a frame is required to exist in principle. Even if there is no such necessity, so that there is no uniquely correct
standard of simultaneity, it does not follow that the succession of time is unreal. On the contrary, all of the experiments (both in thought and practice) that establish the theory of relativity presuppose such succession, where a light signal is necessarily sent before it is received, traveling at a velocity that is the same in all frames of reference. The relativity of simultaneity, with its concomitant phenomena of time dilation and length contraction, results from the attempts of each observer to correct
for the time taken for light to reach him from a distant location. Since the speed of light is the same even to observers moving with respect to each other,[3] their constructed chronologies for distant events will not agree. Yet these chronologies are only formalistic constructions in the first place, and need not correspond to any potentially real succession of time for the spacelike-separated events that have ambiguous temporal order.
Every event whatsoever in the universe is part of a timelike succession, in fact a whole range of possible timelike successions spanned by its light cone. An object that supposedly does nothing, being at rest in a certain frame, is depicted as a straight line in Minkowski space, representing a continuous succession of states in its proper time. Each event has an absolute past that is frame-invariant in scope, and it can only be affected by events in that past. The relativity of simultaneity for spacelike separated events does nothing to compromise the reality of this succession, since such events cannot possibly belong to a common timeline (i.e., a timelike interval or world line). Moreover, we shall see, even if the effects of such spacelike separated events should eventually converge, no ontological ambiguity shall result. After all, even if it is a matter of ambiguity whether astronaut A or astronaut B left his home system first
they cannot fail to agree when they meet that that time is the present
or now.
This is not some fortunate mathematical coincidence, but is built into the presuppositions of the relativistic construction of spacetime. When we map
spacetime, we are not depicting some substance abstracted from measurements, but are depicting the paths traversed by signals in their actuality. It is from these ontologically actual signals that we are able to construct our more formal notions of simultaneity.
We can see more clearly how there is no existential ambiguity implied by relativity of simultaneity by considering some concrete examples. Once this is done, it should be apparent that the supposed ontological problem of relativity is non-existent. The fact that a pair of events can be considered simultaneous in one inertial frame and successive in another does not abolish the objective reality of temporal succession, since this ambiguity obtains only between spatially separated events observed from a third event, so that they are definitely in the absolute past of the third event. There is never a scenario where we get contradictory findings about the ontological status of an event, i.e., having occurred or having not yet occurred. There is nothing in relativity that is incompatible with the reality of temporal flow or succession. Interpretations that deny either the reality of temporal succession or the relativity of simultaneity are solutions to a non-problem.
Relativity of simultaneity obtains only between events that cannot be causally related to each other even in principle. If A and B are spatially separated, A is not in the future light cone of B nor is B in the future light cone of A in any frame of reference. Thus the relativity of simultaneity does nothing to obstruct
any flow of time between A and B, since they cannot possibly be in the same world line (timelike interval) in the first place.[4] An observer may define B to be later
than A or vice versa depending on choice of reference frame (and synchronization convention), but this is a formalism with no physical implications, since these events cannot exist along the same timeline (world line) in any frame. They cannot cause or even receive signals from each other, so their simultaneity or priority is defined only by convention.
None of this prevents time flow, which is to say physical process or motion, from occurring in a continuum of event-points on timelike curves, which is to say all events that can be causally connected.[5] There is no problem of relativity of simultaneity for timelike-separated events. All such events, by definition, are non-simultaneous (one is in the past of the other), and they are non-simultaneous in all reference frames.
The absence of existential ambiguity in relativistic physics can be seen by considering different diagrammed scenarios. As always, we must remember not to treat Minkowski diagrams as something that authorizes to make statements about the entire universe at once. They are just tools for constructing what the expected measurement results will be for observers at a given point in various reference frames. There is no observer-independent, frame-independent reality. The relational structure of spacetime and the laws of physics are indeed frame-independent, but ultimately even these are statements about measurements that can be made by observers at definite event points in definite reference frames.
Suppose you have two observers at the same location and time defined by O, but in different reference frames (relative velocities), so we call them O and O'. [Refer back to Figure 5.] They may disagree on whether some event A occurred before or after event B. If they can observe events A and B, that very fact proves that both of these events are in the past light cone of O/O', so their ontological status is not ambiguous. It may be ambiguous whether A or B happened first, but A is spatially separated from B, so there is no frame of reference in which A and B are connected by a timelike interval, so this has no physical implications.
If events A and B are outside the light cone of O/O′, then they cannot be observed from O or O′ and any judgment as to whether A or B has happened yet is purely formalistic. In fact, you will not be able to observe A or B until some time in the future of O or O′. It is physically meaningless to ask about the ontological status of A and B at the place-time of O/O′, since these events (A, B, O) cannot have any physical effect on each other, nor even be observed from each other. You can only reconstruct a formally defined simultaneity post hoc.
Perhaps the two observers are not at the same location O, but at vastly different locations P and Q in spacetime. Surely, in general, they may disagree on whether some event B has occurred yet [as in Figure 6], but who is to say that observations made at P and Q are simultaneous? You would have to establish that in order to have a genuine paradox regarding the ontological status of B.
In general, any two events P and Q are either related to each other by a timelike interval or a spacelike interval.[6] If timelike, take Q to be in the future of P. There is no paradox if someone at Q observes B but someone at P can not. There would only be a paradox if somehow a person at P could observe B but one at Q could not, since that would mean B could be in the absolute past of P and P is in the absolute past of Q without B being in the absolute past of Q. But this is impossible under the Minkowski pseudometric.
Suppose instead that the observers at P and Q are connected by a spacelike interval. Then there is no way for P to communicate to Q or vice versa; only to one or the other’s future. Whether P is prior to Q or vice versa, or if they are simultaneous, is a matter of arbitrary convention. Thus there is no paradox if they should disagree on whether some event A or B has occurred.
This would be paradoxical only if you treat Minkowski spacetime as a map of what the universe looks like at once, surreptitiously reintroducing absolute time, pointing first here, (P) then there (Q), and showing that they disagree on the ontological status of A and B. Such disagreement is paradoxical only if you can intelligibly speak of distant objects (at P and Q) unequivocally existing at once, which is precisely what relativity denies. Physically definable reality is constricted within observation. We can only define simultaneity from definite perspectives. This constriction of scope is a move away from the arrogance of the nineteenth century, when scientists thought they could understand all reality as it truly is.
Those who hold that the relativity of simultaneity implies an ontological equivalence of all points in spacetime, without any distinction among past, present, and future, are actually relapsing to a pre-relativistic view on a more fundamental level. They refuse to confine physical reality to what is observable, and try to make statements about the reality of physical facts abstracted from determinate perspectives or frames of reference. As we have noted previously, the only frame-invariant aspects of physical reality under special relativity are relational, i.e., the laws of physics and the Lorentz transformation. Facts or events are knowable only through observation from a definite perspective. It is likewise pre-relativistic to insist that reality must be conceived statically in order to be made intelligible. Mistaking Minkowski diagrams for static maps of the universe, it is forgotten that a world line is actually a graph of the present (here-and-now) for each object.
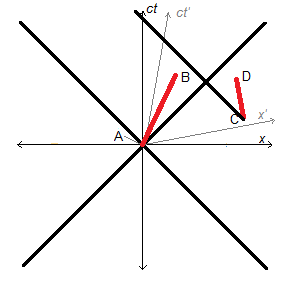
Let us take two different world lines, one from A to B, and another from C to D. So B is in the future of A and D is in the future of C. In order for there to be relativity of simultaneity, there must be some spacelike separation somewhere. Say that interval CD is so far off to the right of AB that A and B are both spatially separated from both C and D and vice versa. [See Figure 7] So an observer at A or B may not know whether C or D has happened yet. So what? It is physically impossible for an observer at A or B to receive any signal from C or D. This changes nothing from what we have said previously. The relativity of simultaneity only obtains between spacelike separated events. Within each timeline, AB and CD, there is no ambiguity.
More interestingly, suppose that D is in the future light cone of A, i.e. the line CD crosses the right half of the future light cone of A. [See Figure 8] Also suppose that B is further up
than D, so that B is in the absolute future of D.
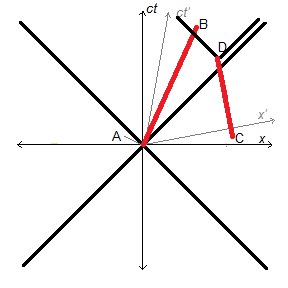
In this scenario, D can observe A, and B can observe D. By extension, C is also in the past of B. Relativity of simultaneity only exists between A and C. Depending on reference frame (relative velocity), observers at B/B’ may disagree on whether C occurred before or after A, even though both C and A are in the past of B. This does nothing to abolish the ontological well-definedness of temporal succession in each world line. It is just impossible to coordinate these into a single correct
chronology for spatially separated events A and C. Any definition of simultaneity you choose is frame-dependent.
Minkowski diagrams are not essential to special relativity, and add no physical content to the theory. Nonetheless, their use can have a psychological impact, as time is represented spatially and statically, leading many to suppose that this is a true picture of temporal reality, or rather unreality. We must recall, however, that Minkowski spacetime is only pseudometric, so it is not truly analogous to a four-dimensional volume, and its invariant distance
is not a distance at all in the mathematical sense. Further, the Minkowski representation is just a succinct reformulation of Einstein’s theory, which was derived from suppositions that assumed the reality of change and a succession of events in time. It is only by rejecting a static notion of length, and instead regarding length as something inferred from signals sent from each end of an object, that we can comprehend the relativistic view of spatiotemporal reality. Under relativity, even space is not static; much less is time.
Treating Minkowski spacetime as a four-dimensional block universe
is fundamentally anti-empirical, as we can never observe or experience the universe as a block. An observer cannot be in more than one place at once, as superphotonic travel is impossible, so we cannot simultaneously
judge what the universe looks like from two different points on the map.
It is illogical to make an inference from relativity that contradicts a postulate of relativity, and indeed the invariance of light speed would be tacitly contradicted if we allowed faster-than-light communication between distant observers.
Minkowski diagrams are useful primarily for giving a geometric representation of the conversion factors for length contraction and time dilation between reference frames. This ability to superimpose reference frames gives the impression that we are seeing something of reality beyond any reference frame, and indeed we are, at least as far as the invariant quantity s2 is concerned. Nonetheless, we cannot say anything definite about space and time without first choosing a reference frame, much as we must choose a coordinate system to define any geometric quantity. The use of Minkowski diagrams does not authorize us to disregard the content of the theory of special relativity and reintroduce a frame-independent, all-at-once view of the universe.
Einstein often spoke as if past, present, future are all relative, and indeed they are, in the sense of being defined by perspective, i.e., where one is situated in space and time. This is not the same as saying that temporal succession is unreal. While we cannot unequivocally coordinate the present here
with the present there,
all events follow other events in local temporal successions. Ordinarily, we might represent motions as graphs in Cartesian space representing the spatial path, with time being represented as a parameter. The Minkowski representation depicts time instead as though it were an extension. A mere change in representation does not add physical content. All representations or models refer back to the synthesis of experimental observations on which they are established. We always measure at a time judged to be the present, which nonetheless we judge to be some duration later than a previous present.
A world line, therefore, is but a graph of all the successive presents
of an object. We can only depict past
and future
relative to each point. So when we show the absolute
past or future, this is always understood to mean relative to the point chosen as the origin. All points in a Minkowski diagram are present,
considered from their own perspectives, i.e., when we choose them as the origin or when we make an observation there. Yet we cannot simultaneously make more than one point the origin, so we are not saying that there is a universal present. Indeed we should expect not, since the Minkowski space is just another graphical representation of the same theoretical content of special relativity. If it added any new physical information, it would constitute a different theory that should need to be tested empirically.
Any two intersecting world lines in a Minkowski diagram necessarily have a common present
at the point of intersection, precisely because a world line is a graph of all the presents
of an object, not just a path of motion as in a Cartesian graph, with time as some extra parameter. To make this distinction clear, consider two intersecting paths of motion in the x-y plane. Depending on the time parameter of each motion, i.e., how fast each object is moving along each part of its path, the two objects may or may not reach the point of intersection at the same time. Furthermore, in a non-relativistic context, we can univocally define that both motions start at the same time t0, but such synchronization is frame-dependent under relativity. How, then, could we hope to know in advance
whether the objects would meet at the same time?
A Minkowski diagram does not abolish the reality of such problems, but instead presents a different class of information. Time is not a parameter of a spatial path, for indeed we cannot know a path length absolutely without reference to some time measurement (inferred from our assumption of the invariant speed of light signals). If we attempted to depict time as a parameter, we would run into the problem of how to make the parameterization of distant paths compatible. Minkowski diagrams instead simply map the successive presents of each object, without imposing a single scheme of synchronization. We can, to be sure, define a relative priority of spacelike separated events for various choices of axes corresponding to different reference frames. One thing, however, remains true under any reference frame: objects with intersecting paths reach the point of intersection at the same time if their world lines intersect, and at different times if their world lines do not. If they do not reach that point at the same time, then it is unambiguous which object arrived first. What is a matter of reference frame is how much time elapsed between the two events. Indeed, we have taken some liberty in speaking of the time
or the point of intersection,
as though there were some identifiable static ether that could define these unequivocally. In fact, these are always defined in some reference frame, and by default, the orthogonal axes of the Minkowski diagram represent the rest frame of an object at the origin.
Minkowski spacetime is not a metric space, since the pseudo-distance function s2 is not positive definite. The invariance of s2 does not mean that space and time are really the same thing in some four-dimensional extension. Their categorical difference is more clearly indicated in Minkowski’s convention of representing time in imaginary units. Rather, the invariance of s indicates an interdependence of time dilation and length contraction, whereby one’s perception of duration versus distance between observed events varies according to the relative velocity between observer and observed.
Notwithstanding such disagreements about the durations between observed events, each observer has his own real physical experience of temporal duration defined by one’s rest frame. Likewise, force experienced is that which is defined in the proper frame (comoving with us so our acceleration is zero at present). Describing physically real experiences, like the magnitude of force we feel in a car crash, requires taking the rest frame and the present as the locus of actuality. The present is about as really real as it gets. What is formal and constructed is not the here- and-now present, but attempts to correlate our present with distant presents and call them a single now.
As discussed at length elsewhere, the mathematical construct of spacetime
does not abolish the ontological distinctness of space and time, though it accentuates their interdependence. Even if we were to treat such a four-dimensional continuum as a single physical entity, however, it would still be a mistake to interpret Minkowski diagrams as a map of spacetime that can be viewed or defined at once, as David Bohm discussed at length:
Because of the relativistic unification of space and time into a single four-dimensional continuum, there is a tendency to interpret the Minkowski diagram as representing a kind of arena or field of action, the whole of which an observer can actually see at any given moment. That is to say, almost unconsciously, one is led to adopt the point of view of an observer who is, as it were, standing outside of space and time, surveying the whole cosmos from beginning to end, as a man in an aeroplane surveys the landscape beneath him. The world lines of other observers then tend to be thought of as tracks traversed by these observers, much as a railway train observed from an aeroplane would be seen to progress along its own track.
A little reflection, however, shows that this view of the Minkowski diagram must be very far from the truth indeed. Consider, for example, an observer at rest in the laboratory, whose worldline is given by OA… At each moment such an observer is to be represented in the diagram by some point such as P [along OA]. Such an observer cannot survey the whole Minkowski diagram. On the contrary, he can only know of events that are inside his past light cone [with respect to P]. Therefore, both his absolute future and his absolute elsewhere are unknown to him.
The real situation, as experienced by an observer at some moment P, is indeed strikingly different from what is shown in the Minkowski diagram. Not only is an observer’s knowledge restricted to the part of the Minkowski diagram that is in his absolute past, but even more, he never sees his own past actually happening, as it is represented in this diagram. For at any given moment we are only experiencing what is actually present at that moment. What we see at a given moment as past no longer actually exists at that moment. What is left of the past is only a trace, existing in the present.… From these traces we reconstruct the past in our thoughts… just as the photograph of a past event is not that event itself.
On the basis of our knowledge, not only of immediate events and facts from the past, but also of general regularities, trends, and laws that have been abstracted… we are able to project a probable future. But while we are projecting it, this future also does not exist. It is in fact nothing more than an image, an expectation, a thought. If our projections are well founded, then the actual future, when it comes, may be close to what was expected. But, generally speaking, our projections are often very wrong, either because our knowledge of the laws and regularities of nature is inadequate, or because our knowledge of the relevant facts is inadequate. Moreover, it is clear from our general experience that all such predictive projections are subject to contingencies, i.e., to factors originating outside the domains that are accessible to our investigations at a given moment…
An important example of the significance of contingencies is provided by the theory of relativity. Thus, as we have seen, an observer at a given moment P can have information only about what is in his absolute past. Even if he is in communication with other observers, he can only hear what they have seen in their absolute pasts, at times which are also in his absolute past.…
Even if we have some fairly reliable knowledge about the general laws of nature… it seems clear that we cannot avoid contingencies, just because we cannot know completely and with certainty what is in the absolute elsewhere. For example, if… an observer P has seen a particle moving on a worldline OV in his absolute past, he can reasonably assume that the particle continues to exist on… the extension of OV into the region outside the light cone of P.… But this projected picture is always subject to contingencies, because something unknown to P may always be taking place in his absolute elsewhere…
It can be seen that all these considerations arise out of the need to take into account the important fact that the observer is part of the universe. He does not stand outside of space and time, and the laws of physics, but rather he has at each moment a definite place in the total process of the universe, and must be related to this process by the same laws that he is trying to study. As a result, because of the very form of these laws physics, which imply that no physical action can be transmitted faster than light, there are certain limitations on what can be known by such an observer at a given moment.[7]
Note that reality is defined in terms of experience. This is an essentially empiricist understanding of physical reality. Attempts to situate reality in the Minkowski diagram as a whole are fundamentally anti-empirical. Each observer can only map his absolute past, and even this map depends on indirect deductions, assuming a convention for simultaneity in his reference frame. Knowledge of what happens further along another world line (i.e., past the point from the last event for which we have information) depends on future contingencies. So nothing changes from classical thinking: we can know only the past; only the present exists for us; and the future is knowable only as contingency. There is no inconsistency introduced by relativity of simultaneity, since that does not apply to events that can be in each other’s past, present or future. It applies only to what is even more abstractly constructed than our absolute past.
Signal path length and frequency, in the relativistic domain, are not simply observed, but reconstructed, taking into account the effect of the time needed for the light signal to reach the observer. It is through such reconstruction that each observer may make a space-time map of events in his absolute past, though the orientation of the space and time axes depends on his frame of reference. Minkowski diagrams are maps only in the sense of giving the structure and order of spatiotemporal events relative to each other for various frames of reference, but they do not show us the world as it actually is.
Such an expression would reintroduce a universal present, but the only presents
are each space-time point as it is taken as the origin. Although Minkowski spacetime shows all such presents in relation to each other in terms of the pseudometric invariant s2, it does not authorize us to combine them all into a single present. Indeed, the reality of temporal succession remains signified by the well-ordered values of the time variable. Our aesthetic choice to represent time in a diagram statically does not bind us to say that time is static, any more than its pictorial representation as extension requires us to consider it as an extension, which indeed cannot be the case.
If two events succeed each other in some arbitrarily small timelike interval, there is no frame of reference in which they are absolutely simultaneous. That is to say, there is no frame of reference in which the reality of their temporal succession is denied or contradicted. Observers may only disagree on the duration versus spatial distance between the two events.
[1] Naturally, we may make calculations for reference frames that do not correspond to the motion of any actually existing observer. In that case, however, we are only calculating the measurement values that a hypothetical observer in that frame would find, not the measurement values that we or anyone else may observe. Notably, it is impossible to define a reference frame for an impossible motion (superphotonic) or an impossible state of rest (i.e., rest frame
of a photon). The notion of reference frame, therefore, is necessarily bound to the possible motion or rest of an observer.
This does not mean that an observer can only take measurements from his own reference frame. Observers in different reference frames may communicate, as when a passenger in a moving vehicle sees a clock outside the vehicle, and may compare this reading with his own watch.
[2] For a detailed discussion of such thought experiments, refer to any standard text on special relativity. For example, when discussing moving clocks, A.P. French reminds us, ‘The time’ is not a metaphysical abstraction, it is the reading on a clock.
[A.P. French, Special Relativity (New York: W.W. Norton, 1966), p.94. When introducing the scenario of a ground observer perceiving light flashes from the ends of a moving train, David Bohm notes that, instead of supposing absolute coordinates in an unknowable ether, all our actual knowledge of space and time coordinates of real events is based on, at least in principle, observable relationships of physical phenomena to suitable measuring instruments.
[David Bohm. The Special Theory of Relativity (New York: W.A. Benjamin, 1965), p.54.] There is no physical knowledge of space and time apart from such measurement.
[3] It should be recalled here that the invariance of the speed of light is a postulate, not something provable. The conceptual difficulty of this speed being frame-invariant is the fact from which all other oddities of relativity spring.
[4] We might consider the finiteness of the speed of light to be an effective obstruction
that prevents space-like events from being causally connected. It is important to insist, however, that the speed of light is not merely an idiosyncratic limitation of a class of particles, but a feature of the relational structure of measured space and time. Expressed pseudo-geometrically, travel at light speed is the shortest possible path.
[5] The geometry of relativity assumes that time is continuous, but relativity has not been validated at the Planck scale, where it is conjectured that time might be grainy or have discrete moments. In order to speak intelligibly about the spatiotemporal relations between events, it is necessary to consider the internal spatiotemporal structure within each event as negligible in scale (compared to the space and time scales between events). This is what justifies representing events as points
in spacetime.
Some have thought to correct this approximation by replacing world lines with world tubes
with the diameter of the moving object. This adds no mathematical rigor, and in fact contradicts relativistic geometry if the tube cross-sections are treated as planes of absolute simultaneity.
[6] For current purposes, we may regard null intervals (travel at light speed) the same as timelike intervals, though in fact such intervals may require a unique interpretation, without duration or length, as discussed in Basic Issues in Natural Philosophy, Sec. 14.1.3. At any rate, the relativity of simultaneity does not apply to null intervals. If anything, they are more absolute
than timelike intervals, due to the frame-invariance of light speed.
[7] David Bohm. The Special Theory of Relativity (New York: W.A. Benjamin, 1965), pp. 173-77.
© 2018 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
| Home | Top |