[Full Table of Contents]
15. Types of Physical Movement
15.1 Change in General
15.2 Movement as a Type of Change
15.3 Accidental and Essential, Direct and Indirect Movement
15.4 Movement as Change between Contraries
15.5 Factors in Movement
15.6 Ontological Categories Admitting Movement
15.6.1 Can Substance Be a Terminus of Movement?
15.6.2 Can Relation Be a Terminus of Movement?
15.6.3 Can There Be Movement of Movement?
15.6.4 Local Motion and Its Derivatives
15.6.5 Movements in Quality, Quantity and their Relations
15.6.6 Movements Between Categories
15.7 Species and Unity of Movements
15.8 Regular and Irregular Motion
In our discussion of relativistic spacetime, we concerned ourselves only with local motion. In relativity, time and space measurements are interdependent, so time is there considered solely as the measure of local motion rather than some other kind of change. Yet it is certainly possible for there to be other kinds of change besides local motion, which is further evidence that time is not to be confined to the spacetime construct, dealing only with certain classes of measurements. We noted in Part II that Aristotle had a broadly defined notion of movement (kinesis) that is a continuous process between definite start and end states. These end states can be defined not only by location, but also by quality, quantity, or substantial being. We further noted that relational states may define movement, as the modern ontological notion of relational accidents is considerably broader than Aristotle’s relatives.
Movement would not be something susceptible to physical explanation if it were a mere happenstance succession of states. What makes a movement physical is some underlying physical principle that accounts for this particular succession. Any account of movement that is situated in time and causal (i.e., giving physical explanation) must make use of some version of the concepts of potentiality and actuality. Movement is the actualization of a potential qua potential; i.e., it is the realization or exercise of some physical power to bring a particular end state into being. Yet this realization is not perfect or completed, or else it would not be movement. Something is in movement only as it is in transition, which is why we add the qualification qua potential.
If something is undergoing qualitative alteration, movement is activity insofar as something is alterable, i.e., has the potential for further alteration.
Change or metabole is an even broader concept than movement, since it contains no assumption about continuity of variation, nor even about whether there are end states with positive existence. Aristotle’s use of the terms kinesis and metabole is not always clear and not always consistent (sometimes excluding substantial change from kinesis), but he provides enough material to help us develop an organized approach to the topic, rearranging and amplifying his presentation.
The basic intuition of change can be gleaned from the Greek metabole and the Latin transmutatio. Metabole comes from bole, a throw,
so metabole is a throw after,
i.e., one thing after another. Similarly, the Latin transmutatio comes from mutatio, which is to exchange one thing for another. Transmutatio would be to exchange across,
i.e., to pass from one thing to another. Inherent in the notion of change is that there is some other thing
different from the initial thing, so there must be some sort of negation or opposition between these two things; they cannot be identical. On the other hand, in cases where something is a subject of change, i.e., some existent X (the subject) changes into another existent Y, it would follow that something of the subject (X) remains constant throughout the change. We have called this matter
in a highly generalized sense. (Part I, Ch. 2)
The sequence of change, in which one thing comes after
another, is that of time in the most generalized sense. In fact, it may be said that we define time with respect to change, and that without change we would not perceive any elapse of time.
Change, considered in itself, is not a subject, i.e., a definite being, though it may happen to subjects. By itself, abstracted from its subjects or objects, change is the process of one thing replacing another, expressible as a sequence of successive states, though perhaps not identical with that sequence. Speaking of change as a noun or substantive can be misleading, as that makes it sound like a static essence. Change is a process of becoming (either categorically or in a certain respect), not being. As we shall see from Aristotle’s extensive discussion of change, it is far from true that he was limited to static essentialism, incapable of seeing the world as process. If he did not adopt Heraclitean or modern process ontology, it is only because he recognized that it is senseless to think that we can have becoming without being, not because he denied the reality of becoming.
Taking the broadest possible view, we may consider four kinds of change, depending on whether or not each of the termini is something susceptible of positive existence. By speaking of termini, we are not restricting our view of change to that which has definite ends, but rather we recognize that any true change must involve a minimum of two distinct things in sequence. For now, we abstract from the question of whether change involves continuous variation or discrete jumps.
Aristotle uses the term hypokeimenon (Lat. subiectum) to refer to that which is affirmatively expressed; i.e., that which is susceptible of existence. It may seem that this reference to subjects
mistakes grammar for ontology, but as we saw in the Introduction to Ontological Categories (Parts I and III) and in Logic and Language (Part I), Aristotle subordinates grammar to ontology, using it to express, not to prove, ontological insights. His approach to definitions is to begin by asking: What do people mean when they say X?
In other words, what reality is our verbal expression intended to indicate? When we express something as a grammatical subject, we are affirming that it is something that at least in principle can be affirmed to exist, though, depending on the particular statement, we may deny or modally assert its existence. Even in our statements of denial, we affirm it as something at least conceptually susceptible of existence. When I say Unicorns do not exist,
I implicitly recognize that a unicorn, if it existed, would be something positive, not a mere absence.
When I speak of not a unicorn,
by contrast, I am at a loss to say whether it exists or does not exist, because it is not conceptualizable as a subject. A subject
in the broadest sense can be a substance, property, relation, or state of affairs; i.e., anything susceptible to positive existence. By non-subject,
I mean that we are not positing anything as a conceivable existent, but only positing the absence of some subject. When I say there is not green,
there may be some color other than green, or something to which the category of color does not apply, or nothing at all. All of these contradict the presence of green, but we are not asserting (or denying) that some other thing exists in its stead. We are only denying the existence (in whatever mode we are speaking) of some subject, so we call this ouk hypokeimenon, not a subject,
or non-subject.
That said, the termini allow us to define four logically possible kinds of change:
[Here, subject = hypokeimenon, and non-subject = ouk hypokeimenon (‘not a subject’).]
Since the subject or hypokeimenon in question is a terminus that need not be a substance, it need not have a material aspect that remains constant through the change, even in changes of the first kind. Nonetheless, changes of the first kind are always referable to some substance (since all conceivable subjects are at least referable to some substance as a property or relation), so they will involve some perduring matter
at least implicitly. We should note that ‘subject’ here is not to be taken in the sense of that which has something done to it, as when we speak in other contexts of the subject
of motion, i.e., that which is moved or mobile. Here we only mean that which is susceptible of positive existence, without implying anything about its status as an agent or recipient of change.
Change in the broadest sense encompasses categorical becoming and perishing (the third and second kinds), though we often intend the term change
(in English, as in Greek and Latin) in the more restrictive sense of the first type.
Just as the subject or hypokeimenon is the real thing lying beneath
what is posited verbally, so the antikeimenon lies against
such a subject, i.e., it is other than the subject, being present only insofar as the hypokeimenon is absent. Antikeimenon is often translated as opposite,
but this is in the sense of facing
the subject, being different from it, not necessarily its diametric or polar opposite (called a contrary
). In modern set theoretic usage, we might call the antikeimenon a complement,
or a part thereof, i.e., an entity susceptible of positive existence that is different from the first subject. It is indeterminate, or rather, it is determined only privatively, i.e., as something that exists in the absence of particular hypokeimenon.
In traditional Latin terminology, an antikeimenon is called a contradictory,
since the assertion of its existence implies a denial of the existence of the first subject in the same sense. A particular kind of opposite, called a contrary (enantion), refers to things which differ maximally by some measure, property or relation.
There can also be contradiction between subjects and non-subjects, but contrariety can exist only between subjects. This is because contrariety presupposes some common measure, property or relation by which we can determine a maximal difference in termini. Such definite measures, properties or relations can only obtain among things that can conceivably exist, i.e., subjects.
It might seem that there are some cases where the contrary is a non-subject. For example, the contrary of light is dark, and darkness is an absence of light. Yet, as Aristotle notes, it is not the absence of light as such that constitutes darkness. To offer an example, a sound has no light, but we would not say that sound is darkness. An abstract idea has no physical light, yet we would not say it is darkness. Clearly, darkness refers to the visual perception we have when light is absent. What makes light and dark contraries is their shared perceptibility and their extreme opposition of magnitude in terms of light saturation. The privation or absence of light is only incidentally contrary to light, since contrariety requires more than the mere absence of light. The non-subject not light
is at best improperly contrary to light, though it is contradictory. (Yet it is not really an antikeimenon unless it is susceptible of positive existence.)
The fourth kind of change is not really a definite change at all, since there is no necessary opposition or contradiction between any two non-subjects. Not fire
and not water
may or may not be identical; going from one to the other need not entail any change. Even going from not light
to not dark
need not involve change, for these non-subjects can include the absence of perception.
The second and third kinds of change do not involve contrariety, but only contradictory opposition. A change from a non-subject to a subject is known as becoming.
This can be in an unqualified or categorical sense, as when we say simply, X comes to be,
i.e., comes into existence. Such unqualified becoming is also called generation. Becoming can also be in a qualified or particular way, as when we say, X becomes white,
i.e., it went from non-white to white. In that case, X itself did not come into being, but rather the accident of whiteness in what was once non-white. In either case, there are no contrary qualities, but only the opposition of existence and non-existence.
A change from a subject to a non-subject is known as perishing.
Again, this can be in a qualified or unqualified sense. Unqualified or categorical perishing, also known as destruction or corruption, is when the subject itself passes out of existence, i.e., X ceases to be.
Qualified or particular perishing is when some accident of the subject passes out of existence, e.g., X ceases to be white.
Once more, there is only opposition between existence and non-existence, not contrariety of properties or relations.
Changes from subject to subject are the only kind of change that may have contrary termini. The termini of such changes may also be non-contraries (i.e., contradictories), as when something changes from green to brown.
We can summarize our findings so far in a classification table:
| Metabole = process of A being replaced by B, where B != A (A and B are called termini) | |||
| hypokeimenon = a definite conceivable existent X | ouk hypokeimenon = not Xfor some hypokeimenon X |
||
| antikeimenon = any conceivable existent different from a given hypokeimenon X. Set theoretically, an antikeimenon is any element of the set Xc = {all Y s.t. Y != X} Note: ouk hypokeimenon has no set theoretic representation, since nothing is posited. | |||
| 1st kind Change from A to B, where A and B are hypokeimena |
Termini are (non-contrary) antikeimena | Requires persistent matter | |
| Termini are contraries | Requires persistent matter | ||
| 2nd kind Change from not Bto B | Termini are contradictory (but not antikeimena, for one is a privation) | Unqualified: B does not existto B exists |
|
Qualified: B is not Pto B is P | |||
| 3rd kind Change from A to not A | Termini are contradictory (but not antikeimena, for one is a privation) | Unqualified: A existsto A does not exist |
|
Qualified: A is Pto A is not P | |||
What Aristotle calls qualified
becoming or perishing is really an equivocal usage of becoming and perishing, referring to the appearance or disappearance of some accident P. We will therefore treat becoming and perishing only in the unqualified sense (unless otherwise specified), with the understanding that the terminus that is a hypokeimenon can be a substance, property or relation.
Do the three basic kinds of change always describe really distinct processes, or are these merely formal distinctions? Going from A to B might be formally described as going from non-B to B and from A to non-A. There might be only one real process in this case, and what we call generation and destruction is abstracting from determinate knowledge of one of the termini. In such a situation, we might say that change from A to B involves the becoming
of B and the perishing
of A. For now, however, we will allow that there might be becoming and perishing without reference to some change of the first kind, and that changes of the first kind need not be reducible to a composition of becoming and perishing.
In Part II, we descriptively defined movement
as a type of change between two definite end states via a continuous variation across intermediate states. All physical changes that can be measured in terms of continuous variable observables may be modeled as movements
so defined, making this a broadly useful physical concept. Such continuity of variation implies that something undergoing movement cannot be in the same state for a finite interval of time. (We abstract here from the question of whether time is grainy,
discussed previously, since for all practical purposes the minimum instant
is smaller than time scales we can measure.) The condition of non-movement, or rest, with respect to the same variable implies that the state with respect to that variable remains constant over some time.
It should be noted that not all continuous changes in observable states need be physical movements. If the change is happenstance (unrelated to any underlying physical principle), it would not be a physical movement, though we should think it extremely unlikely that a continuous change would be mere coincidence. On the other hand, if the change is merely in a relative measurement, without corresponding to a real change in physical state, exercising physical power, we should hesitate to consider this a physical movement. An obvious example is so-called inertial motion, which does not appear to involve the realization of any potential; i.e., the activity of any physical power. A continuous change in position over time may be defined in relation to other bodies, but if absolute place has no physical significance we can hardly regard inertial motion per se as a physical movement, i.e., a continuous change in physical state. We defer the problem of how to treat inertial motion to a later chapter.
Since we are concerned only with physics, we restrict our discussion to movements defined by physical states, i.e., states that correspond to something potentially observable. Some physical substance, property, or relation must be posited as conceivably existing in order for us to speak intelligibly about a physical state. It is intelligible to say, A horse is black,
or A horse is white,
but we cannot define any state, even hypothetically, for a non-subject, not a horse.
Thus a non-subject cannot be considered at rest, since this would require it to have a definite physical state for some finite interval of time. If a non-subject cannot occupy a state at rest, much less can it be in movement, since that requires some definite state as a point of departure (terminus a quo). Thus, the second kind of change, becoming,
cannot be a movement, as Aristotle remarks, since it is a non-subject that becomes
some subject.
This appears to contradict Aristotle’s earlier definition of kinesis, which was broad enough to encompass substantial generation and destruction. Yet generation and destruction can be movements only if they are continuous variations, so becoming
and perishing
per se are not movements, since there is no intermediary between A
and not A.
Rather, generation and destruction can be continuous processes insofar as there is some underlying change of the first kind (from subject to subject). The death of a horse is a movement not in the sense of the horse ceasing to be,
but only insofar as the characteristic physical qualities of the horse change continuously (via degradation of vital processes, necrosis, decomposition). Generation and destruction can be movements only insofar as they are accomplished by a transformation from one subject to another. Categorical creation ex nihilo and annihilation cannot be movements, nor is the ceasing
or becoming
of some substance or property a movement, considered in abstraction from continuous transmutation.
Although movements may be potentially infinite insofar as time is potentially infinite, any actually realized movement must be bounded in time. This is why we still define a movement with start and end states, even though we are no longer confined to the ancient Greek notion that physical change is fundamentally between pairs of qualities. The Latin terms terminus a quo and terminus ad quem helpfully denote the start and end states of a movement, indicating that movement has a direction in time from
one state to
another. The termini and intermediate states are what we actually observe or measure, while movement is what we infer from these. The movement might continue indefinitely beyond the termini chosen for observation.
Should the contrary of a movement be considered rest or an opposing movement? Recall that contraries are maximally different with respect to some measure, property or relation. If movement is a continuous change from state A to state B, then an opposite movement from state B to state A would be its contrary with respect to the direction of its trajectory in phase space. Rest and movement are opposed with respect to the presence and absence of variation, which is contradiction, not contrariety.
Although the third kind of change, perishing,
begins with a positive subject, Aristotle holds that this cannot be a movement, because the contrary of a movement is another movement (or rest, which he allows as an improper contrary), while the contrary of perishing is becoming, which is neither rest nor a movement. Does this really follow, or could there be a sense in which perishing is contrary to rest or movement?
Recall that, paradoxically, it is essential to the notion of contrariety that there be something held in common, i.e., some measure, property or relation. For two things to be contraries, they must share a dimension in some phase space. We can easily see how this is the case for contrary movements, by depicting them vectorially. Rest belongs in the same category as movement, since it may be seen as a limiting case of movement, where either the magnitude of the variation approaches zero, or the time required for some finite variation approaches infinity. What contrary could we posit for a movement that is neither a movement nor rest? Once we step outside the category of movement and rest, we are dealing with something that is neither the presence nor absence of variation between two states. Such an entity cannot have the dimension of variation in common with movement, so that leaves only the termini. The other entity might be a contrary to movement in the sense of having reversed termini; i.e., B to A instead of A to B. Yet in that case it has nothing in common with movement save the fact of having termini. The fact of having termini admits no degree; it is either present or absent, so there can be no dimensionality to it. Thus it cannot serve as a common measure or basis of contrariety. Our mysterious entity with termini B and A would not be a contrary of movement from A to B, but something altogether dissimilar and incommensurate. Since becoming
is altogether dimensionally dissimilar and incommensurate with movement, notwithstanding the fact that it has termini in time, it follows that its contrary, perishing,
is likewise categorically dissimilar from movement.
This confirms that only changes from subject to subject, i.e., changes of the first kind, can be movements. The converse does not follow; i.e., not all changes from subject to subject are necessarily movements. There could conceivably be discrete, non-continuous changes from subject to subject. Aristotle frequently ignores this possibility, and uses the terms metabole and kinesis interchangeably when discussing changes of the first kind. We will be more rigid in our terminology, and speak of change
in general only when we are allowing non-continuous changes, while movement or kinesis is restricted to continuous variation.
All movements are changes from subject to subject, and physical movements involve subjects that are physical or natural entities. The termini of movement can be different qualities, quantities, places, or relations.[1] All such accidents presuppose some underlying substantial entity (unless you subscribe to trope theory, in which case accidents are effectively substantial), so there is some physical thing that undergoes movement, the X in the sentence, X moves.
Sometimes the X in X moves
need not refer to the substance itself, but a property or relation of such. Aristotle distinguishes three senses in which we might say that X moves.
The musician walks.Nonetheless, saying
The musical faculty walksdoes not denote physical agency, so incidental or accidental change is not of concern to physics.
Note that accidental
in #1 is contrasted with essential
in #3. This is not the same as a substance/property distinction, though these are sometimes confused in Aristotle (who equated ousia with substance). Obviously, changes in accidents
in the sense of properties are of concern to physicists. We may understand the essence
in #3 to include any properties that are characteristic of the subject. The musical faculty in #1 is accidental
not merely with respect to the musician (i.e., it is his property), but with respect to the change (walking
). The faculty walks
not by its own nature (indeed it is physically senseless to speak of a faculty walking), but by attachment to the musician who does walk. In short, the act of walking can be physically understood without any reference to the musical faculty.
The distinction between #3 and #2 should be understood as that between direct and indirect physical movement. In #2, the subject is moved only indirectly, insofar as some part or property of it is moved. In #3, the subject is moved by some activity proper to it as a physical entity, i.e., by its physis or principle of movement. This principle may reside in essential properties of the subject, so the distinction between #2 and #3 is not between substance and accident (i.e., property), but between direct and indirect agency.
This threefold distinction applies regardless of whether we consider the subject of movement to be the mover or the moved.
It seems that this account of change between subjects is not comprehensive, as the distinction between essential and accidental change assumes an object-oriented ontology, as if change could only originate in inherent aspects of objects. What if a change instead arises from the relational structure between objects? It would seem we need a fourth sense of change, or rather a subdivision of #2, where something changes because one of its relations changes. The difference is that a relation need not depend on a single subject, but on two or more subjects. Relational change is only in #2, not #3, since two-predicate relations are extrinsic accidents.
Even the above clarification seems incomplete, since it does not consider treating relations themselves as subjects of movement or change, as is common in modern mathematical physics. Indeed, as we have discussed elsewhere, physicists frequently treat relational structures, or laws of physics,
as though they had causal efficacy. Yet in that discussion we concluded that such laws are more properly descriptions of the formal natural order whereby the powers of physical agents are defined. Indeed, every field theory, even though it has vacuum solutions, presupposes some source. So we have adequately accounted for relations by treating them as extrinsic accidents; i.e., the relation of the subject to a source. While it is true that we can treat relational structures such as fields as though they were agents, or at least media of physical agency, this only requires us to expand the notion of substance to include fields, for fields so considered would be substantial rather than relational, much like the spacetime metric discussed in the last part.
Physics is only concerned with essential or per se change, not incidental or per accidens change, which can be multiplied without limit, and is not subject to analysis. Accordingly, we will restrict our discussion of movement to per se movement, both in the direct and indirect senses mentioned previously.
Since movement is a continuous variation from subject to subject, its reality implies at least a tendency toward a contrary extreme in the varying property. Suppose we have some continuous variation across states from A to B, where B is not A (i.e., they are contradictories). For some C to be intermediate to A and B, there must be some common property, measure, or relation, modeled by some variable x, by which x(C) is intermediate to x(A) and x(B); i.e., either x(A) < x(C) < x(B), or x(A) > x(C) > x(B). Continuous variation implies we can construct a further intermediate between C and B, and then between these shorter intervals produced, ad infinitum (or at least down to some fundamental unit of time, recalling that the spectrum of states A through B is situated temporally). Now even if A and B are not themselves contraries (i.e., maximally dissimilar with respect to x), it is clear that, in moving from A to B, the subject is moving toward one extreme value of x and away from another extreme, though these extremes need not have definite values (i.e., they could be potentially infinite). In this sense, we may say that all movement is a change from one contrary toward another, though the termini need not be contraries.
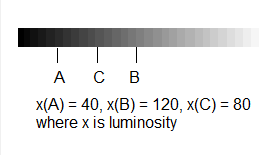For example, an object might brighten only from a dark gray to a lighter gray, yet this movement is toward white and away from its contrary, black. Something becomes more white only insofar as it becomes less black, and vice versa, so even moderate movement may be understood in terms of contraries. In cases where there are no definite extremes, as with local motion in a potentially infinite space, we may characterize the extremes by direction (i.e., left vs. right, up vs. down), without implying that there is a maximum value.
Aristotle thought that some qualities, such as color, had discrete categories, which could be arranged only as contradictories, not as contraries. Yet under the modern paradigm of the mathematicization of physics, all qualities and relations can be modeled quantitatively, so contrariety at least potentially exists wherever there is continuous variation. While Aristotle is correct to admit that the termini of a given movement might be merely contradictory rather than contrary, even these movements presuppose a tendency toward one or another extreme. Since mere contradiction admits no mean, any change that admits a mean must involve contraries at least implicitly.[2]
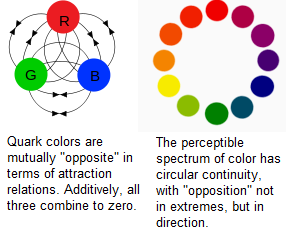Classical discussion of contraries used pairs of extreme opposites, and we have refined this by seeing an implicit contrariety in any continuous dimension, even if unbounded at both extremes. Yet what of non-binary systems? For example, the three quark colors
are all mutually contrary in a sense; i.e., these states are maximally removed from each other with respect to that variable. Also, there may be circular dimensions that do not lead toward remote extrema. For example, the qualitative perceptible color spectrum elides from red to orange to yellow to green to blue to violet to red again. The only contraries
we could define for such systems is not two maximally removed states, but two maximally removed tendencies, i.e., clockwise and counterclockwise around the circle
of states.
It may seem that the question of contraries in physical movement is of purely historical interest, owing to the ancient Greek predilection for describing everything in terms of qualitative opposites, in the absence of a mathematical theory of physics. Attempts to force-fit reality into the paradigm of contraries led to some strange results. Aristotle, for example, had to define the contraries in place to be the center of the Earth and the outermost heaven, rather than admit that local motion involves mere contradictories. Avicenna thought to avoid this awkward solution by using position (situs), which need not have a contrary, instead of place. Thomas Aquinas, on the other hand, saw the lack of intermediaries in situs as proof that there were no real movements or changes in situs.
The use of contraries to characterize movement does add something that would be lost if it were described merely by contradictories. Movement between contradictories would just mean going from X to Y, where X is different from Y. Physics, in that case, would just be one thing after another
with no underlying structure between the start and end states. The intuition of contrariety, on the other hand, describes movement as something that has a direction or tendency, one that is potentially reversible. The spectrum of intermediate states are not related to each other by happenstance dissimilarity, but by an ordering with respect to some common measure. The notion of contrariety, in the broadest sense, may be considered a synthesis of commonality of measure and difference in order.
This can easily be seen for real-valued continuous variable physical quantities. We can model the possible states along the real number line, which is a well-ordered set. We are justified in arranging these states along the same dimension only insofar as they reflect a common measure. A movement can be depicted as a trajectory with direction along that dimension (or in a more general phase space, with each dimension defined by a distinct physical variable). Even this representation is incomplete, however, as movement is something more than a trajectory in phase space. For there to be movement presupposes some underlying subject of movement; otherwise there would be mere succession. Also, there must be some underlying physical principle (the mover
) that accounts for the movement, giving it a causal cohesion that makes it truly physical.
Earlier, we noted that only finite magnitudes can be observed in physics. (Part II, 10) This implies that, for variables that have no definite extrema, such as spatial location, there can be no actually realized contraries. Even in such cases, the notion of contrariety has significance, since we can consider each movement as a tendency toward one or another indefinite extreme (formally denoted as plus or minus infinity). The only difference from systems with definite extrema is that a movement can potentially continue indefinitely.
Our mention of variable physical quantities
or physical variables
refers to any quantifiable physical property, be it quantity, quality, place, or relation. Qualities are quantifiable by intensity or degree; places are quantifiable with regard to the extension of their internal space, or the distance between two points. Relations can admit of intensive or extensive magnitude. In modern physics, it is widely assumed that all physical properties may be modeled quantitatively. While it cannot be proved that this is the case, only such properties are susceptible to analysis. Other kinds of properties, consisting only of contradictories, leave us only with brute facts, or one thing after another.
Aristotle identifies five factors involved in a movement: the mover, the moved, time (that in which movement takes place), the starting state and end state of the movement.
The discussion of time (in Parts III-IV) was a necessary preliminary, since time is an essential factor of movement, serving as a sort of medium or measure of movement, and an ordering principle for the actual sequence of starting and end states. This is not to make time a causal factor of the ordering of states. The ordering of variable physical quantities is determined by the intrinsic formal structure of such properties. The ordering determined by time is the actual direction of the movement in question, whether it is from state A to state B, or from B to A, or more generally, the direction of the trajectory in some phase space.
Aquinas considered time to be an extrinsic measure of movement, therefore not a part of movement. The movement is determined by the mover, the moved, and the physical states, not by time. Time does not determine the direction or magnitude of movement, but measures it. In much the same way, space may measure how much of a substance there is, but space is not part of the substance.
As we noted previously (Part II, 9), the concepts of a mover
and moved
presuppose that movement is fundamentally causal. The mover
is the cause of movement and the moved
is the thing that moves, i.e., the persisting subject that traverses various physical states. There is no a priori reason why the mover and the moved might not be the same thing. In Newtonian mechanics, action and reaction may be considered as two simultaneous opposing movements: object A moves B and B moves A.
Action-reaction symmetry obtains for force relations, but not for transferences of energy. When energy is transferred, there is a real causal asymmetry between the mover and moved. As a simple example, we may apply heat from some burning substance A to another substance B, causing the latter to become qualitatively altered (e.g., charring, melting, boiling). Aristotle considered that only the matter can be moved
or altered. If we are heating wood with burning methane, he would say that only wood considered as matter is moved or altered, for form as such does not change. In other words, when a thing is moved from one state to another, what is moved is that which persists. One form may be replaced by another, but form as such does not change. Wood may change from brown to black, but it would be nonsense to say that brownness
as such becomes blackness.
Rather, the substratum is moved from one state to another.
This account may seem strange. After all, if matter is that which persists, how can it be said to be moved?
It would seem to be unchanging. It is indeed unchanging qua matter, but it does change in the sense of having a new form instead of the old. In modern terms, we may visualize movement as a trajectory in some n-dimensional phase space, where time is a parameter of the curve, and each dimension corresponds to some physical property. Aristotle’s claim that the matter rather than form is moved means that we should not see the movement as one point or chunk of phase space being moved to another place in phase space. The whole notion of moving in a phase space supposes that there is something other than the states (points in phase space) themselves, which cannot move in phase space. That other thing is the subject of movement, and it is called matter, because it is what persists through the changes in state. Note that we are not implying that matter is something that is separable from form. The thing being moved may have other properties outside the phase space which remain constant through the movement. Yet in reference to the movement, the entire subject is effectively material or persistent.
For Aristotle, the introduction of a subject that is acted upon was essential to account for movement. Other philosophers explained movement solely in terms of contraries or termini; e.g., hot and cold, dry and wet. Yet there must also become persistent thing that takes on one or the other property, or we would not have movement, only destruction and creation. Matter, for him, is essential to account for the continuity of movement. Yet we might see the continuity of states as something conceivable independently of a persisting subject. That is to say, the continuum of phase space has a structure that is independent of whatever material thing passes through it, so matter might not be essential to account for the continuity of motion. A trope theorist might hold that the subject of movement is some bundle of properties (external to the phase space) that remain constant throughout the movement. Such an account might face a problem of infinite regress, but we will leave that to metaphysics. For us, it suffices to note that such bundles effectively act as what Aristotle calls matter.
Can there be movement without a mover? If we accept that all changes in the sensible world are explainable, i.e., they do not simply happen de trop, then every physical movement must have a cause, which we call the mover. There is no a priori reason why the mover cannot be substantially and numerically identical with the thing moved. We will deal with self-movement in some depth later.
Regarding the termini as factors of movement, Aristotle finds a curious asymmetry: the end-point (terminus ad quem) but not the starting point (terminus a quo) is essential to movement. A movement is defined by its end, not by its beginning. Terms such as burning,
boiling,
melting,
freezing,
darkening,
all define movement by their end point, or tendency towards an end. This holds even for kinesis in the more general sense that admits generation and corruption. Something perishes because it ends in dissolution. So what is properly essential or intrinsic to a movement appears to be where it is heading, not from whence it departs. Is there really such an asymmetry in physical movement, or is this just an accident of our naming conventions for movements?
The termini as such cannot be intrinsic to movement. Thomas Aquinas clarifies that movement is not in either terminus, but in the subject. He says movement has an attraction to the terminus ad quem and a repugnance to the terminus a quo. In this view, we might consider the termini to be extrinsic accidents of movement. The choice of terms attraction
and repugnance
follow the order of time, as we say a movement heads toward
a future state and away from
a past state. This is not an arbitrary convention, as the time evolution of many systems is asymmetric, favoring more entropic states, for example. Probabilistic and statistical analysis of such systems would not work on the assumption that time was reversed. Granting some physical reality to the fact that all things move forward in time (though the precise direction of forward
may depend on a local frame of reference), the terminus ad quem is in alignment or agreement with the intrinsic tendency of a movement, so it has some similitude to the essence of the movement, though it might not properly be a constituent of that essence.
Since movement is defined at least in part by a tendency toward some future state, we may speak of a telos or goal
of motion, though this is not to be understood as directly implying conscious intention in nature. The final state or telos may be a form, a place, or an affection, according to Aristotle. In any case, these goals are immovable, which accounts for why he was so insistent that place is immovable.
What Aristotle calls affections (pathe) are qualities that a substance may adopt from without. In other words, it is a quality considered as something happening to a substance or body. Affections (pathe) are not movements, he says; e.g., whiteness is not a movement, but whitening is.
It seems strange that Aristotle excludes quantity from possible teloi, though these are possible termini of movement. Perhaps quantity is already implicit, since definite qualities or affections may be defined in part quantitatively, i.e., by amount or degree. He focuses on the qualitative aspects of final states as teloi because this is something that can be considered already intrinsic in the movement before the final state is reached. For example, if something is whitening, a tendency toward whiteness is occurring even now, when the subject is still far from being white. Yet if something is increasing in brightness, it is not thereby tending toward any definite goal. With our modern notion of vectorial quantities, however, there is no longer any need to exclude quantity from teloi, since it is no longer necessary for there to be a definite endpoint in order for us to express a definite intrinsic tendency or direction. We can have indefinite goals.
Something can be a goal or telos in a manner only accidental to the movement. For example, a magnet is attracted to a piece of iron that is being heated. That attraction is only incidental to the movement
of the iron heating or reddening. The example Aristotle gives seems dubious at first: a thing becoming white accidentally becomes object of thought. Here he uses the telos of human intentionality of thought as though this were equivalent to that of nature. This is not because he thinks nature is conscious. Rather, he considers human intentionality to be just a special case of the teleology found in all of nature. In any event, the possibility of accidental goals shows that we cannot regard something as a true physical telos simply because a movement ends there. What makes something a telos of movement is that it is intrinsic to the tendency of movement even before the goal is reached.
Aristotle lists the following ontological categories, to examine which of these admits movement:
Being, Quality, Place, Time, Relation, Quantity, and Activity or Passivity
Only eight of the ten from the Categoriae are mentioned here. He omits position
(relative disposition of substantial parts) and state
(relation of an object to certain qualities), which we have identified as types of relations. (Introduction to Ontological Categories, V) Aristotle contends that only three categories admit movement: quantity, quality, and place.
The omission of time is easily understandable, since time is the measure of movement, not the thing that moves or changes. It is less obvious if the exclusion of other categories is justified.
Aristotle denied that substance can be a terminus of movement (in respect of substance there is no movement
), since substance has no contrary, except in the equivocal sense that an absence is a contrary. This does not mean that substances do not move. Rather, a substance can move only in its accidents; i.e., it can vary in place, quality or quantity. You can line out the values of these accidents in a continuous spectrum of movement over time, but cannot do the same for substance. Once a substance has ceased to be that substance, it would no longer be the subject of movement (or anything else!).
This is clear enough if we regard substance as simple being, but perhaps there might be movement between so-called substantial forms, i.e., configurations of essential properties that define species of substance. Invoking substantial forms does not require us to make a judgment about the reality of universals, except that the real exemplification of such forms in individuals implies some reality of the species (and vice versa). This does not mean that a species or substantial form has the same sort of reality as a property or universal accident. Even if substantial forms define classes of substance, primary existence belongs to individual substances, which are not mere instantiations of universals, since they can also have non-essential properties.
Aquinas did not think there can be movement between substantial forms, for once something loses its substantial form, there is nothing preventing it from taking on any other form. It is not necessary for it to traverse all intermediate
forms. This depends on the metaphysical claim that there are discretely numerable substantial forms, rather than a continuum of possible forms. Aquinas invokes arguments in the Metaphysics that the common root of all contrariety in various genera is that between excellence and defect (i.e., abundance or lack of some property).
Further, Aquinas notes, the subject of a substantial form is merely a being in potency. Thus, we may gather, the movement
of a substance between two forms would not have an actually existent subject. If the subject is not actual, neither can its movement be. This contention, however, seems difficult to reconcile with Aristotle’s definition of movement as the actualization of potency qua potency.
Although the Scholastics rightly denied that there can be degrees of possibility, there might nonetheless be potentiality as a real power of bringing something into existence, and such potentiality could vary continuously by degree, as it is something more than bare possibility. The quantum mechanical phenomenon of neutrino oscillation may be taken as an example of a change between discrete substantial forms (those of an electron neutrino and a muon neutrino). Though there are no actual intermediate forms to traverse, the potentiality to manifest one or the other form varies continuously in a sinusoidal function over time.
Although we shall see that movements can be relative, they are still in the categories of their termini, be they substances, qualities, quantities or locations. This leads to the question of whether relations can be termini of a movement. Why does Aristotle exclude relation as something that can admit movement? As usual, he seems to restrict relation to pairs of relatives
such as double and half, master and slave, which are obviously not objects of physical change, since they have no existence apart from their formally defined relation to their correlate. How can double
as such become anything other than double? Yet if we expand the notion of relation to include position and all other kinds of relative accidents, it is scarcely avoidable that relations may be the termini of change. Indeed, modern physics has shown that nearly all measurable properties are relative in magnitude, and the strengths of forces are determined by relative accidents rather than absolute place or speed. While change in place is certainly possible, and there might be such a thing as absolute place, the only thing that is physically relevant is change in relative distance, velocity, etc.
Following the principle that a movement is in the same genus as its termini, Aquinas held that movement cannot be in the genus of relation, even relations such as situs or habitus. The reason is that relations do not change without their terms changing, so the category of movement must be in the category of those terms, be they substances, quantities, qualities, or places. Aquinas, like Aristotle, conceived of relations or relatives only as inherent accidents.
Relation may be considered more broadly as a higher-order accident, i.e., as something predicable of two or more accidents, without inhering in any particular subject. A simple example of such a relation is the distance function D(x, y), where x and y are positions defined in some frame of reference. The magnitude of D may change with the terms x and y, but this does not constitute changing into a different kind of relation. The use of quantitative relations in physics does not ordinarily imply the relation as such to be changing. On the contrary, we assume the relation to have a constant definition in order for comparisons between different sets of terms to be valid.
Aquinas remarks that a relation changes only per accidens, e.g., from equality to inequality, by change in quantity of the terms. [Comm. on Physics, 666] Equality as such does not become inequality as such. Can there be cases where the relation itself changes? If so, on what basis would it change?
We should introduce some formalism from mathematical logic to clarify the discussion. In first-order logic, terms or subjects can be represented as variables or arguments, while formulas representing propositions are of the form P(x1, x2,... xn) (and more complex statements using logical connectives), where P is a predicate symbol and xi are arguments (variables or constants) representing terms. Ontological relations or relatives can be represented as predicates with two (or more) arguments.[3]
Q can represent the ontological relation is a divisor of,
in which case Q(x, y) is true if x is a divisor of y, and false if x is not a divisor of y. These kinds of relations correspond to classic Aristotelian relatives or correlatives.
Some relations can be symmetric, so that R(x, y) ↔ R(y, x) for all x, y. An example of this is the distance between two points. Since x is R from y
is equivalent to y is R from x,
R can be considered as not preferentially predicated of x or y. x is 5 meters distant from y
is the same as y is 5 meters distant from x,
so we can just say x and y are 5 meters distant.
Ontological relations may be regarded as accidents of composite subjects, not as parts, but as ontologically dependent on a plurality of components.
There can be higher-place predicates. Some ordinary language examples: I gave a ball to her.
I placed the rock on the table.
The indirect object acts as a third term. Giving
or placing
are defined in relation to all three terms. Three-place predicates need not be restricted to this subject, direct object, indirect object structure.
With this groundwork laid, what can it mean for there to be a change in relation? In ordinary first-order logic, the terms can be constants or variables, while the predicates are constant. This does not mean that the predicates cannot have different values; after all, a predicate is a characteristic function of a set-theoretic relation, so it can take the values of 0 or 1.[4] The predicate itself does not change from one predicate to another. Is there a way we can amplify first-order logic to allow for such a change?
In first-order logic, time is representable as a sequence of states (though ontologically time is much more than this). Perhaps we can introduce a variable that represents the state of a relation at various points in time. For the two-place predicate S(x, y) (representing an ontological relation), we can add another variable defining the state of the predicate S at a given point in time, so the changeable predicate is defined by x, y and this state s. A state can be constant or the result of action. Since we are explicitly assuming non-constant states, this must be the result of some action.
One may object to this formal possibility on the grounds that this is ontologically unsound. A subject is what its predicates are, so variable predicates constitute a variable subject.
[5] If we take a simple one-place predicate, e.g., green
in A leaf is green,
and allowed that it could vary in value (e.g., ranging across various shades), what is really changing is the subject, the leaf,
taking on various predicates. It makes no sense for the predicate as such to change. The predicate exists only insofar as the subject exists.
It may be countered that this subject-predicate ontology is itself unsound; in empirical science, all we really observe are properties with different values. The existence of a property-bearing subject is a gratuitous supposition ill-supported by physics, and possibly contradicted by quantum mechanics. Yet this trope ontology would only build subjecthood into what we call properties, and is not really different. A predicate (or the accident it represents) remains changeable only insofar as it is a subject (representing something susceptible of primary existence).
So-called variable predicate calculus or logic of variable predicates (LVP), as applicable to physics, does not entail predicates changing over time. Rather, it considers variations among possible predicates across different models. In limiting cases, such variation can lead to a qualitatively different physical model, as in quantization. Shah and Yourgrau (1978) argued that the dependency of truth values of physical theories on experiential data makes LVP useful. As experimental results change, so do the truth values of various models, and these values may not be definable at critical points. LVP enables us to say a limiting variation of a property is not a change to an altogether different property.[6] Whatever the merits of this position, this is not the same as asserting that a property represented by a predicate changes qualitatively over time. On the contrary, this calculus would make it unnecessary to regard even variational change
as entailing a change between two categorically distinct predicates.
We may follow Gottlob Frege in treating relational motion as a two-place predicate, and considering the meaning of a complex expression as fully determined by the structure and meaning of its constituents (whether or not this is true in general). Defining such two-place predicates as follows, we can have true motion without absolute motion.
Relative position: P(x, y) is the position of object x with respect to object y.
Relative velocity: V(x, y) is the velocity of x with respect to y (i.e., in the frame where y is at rest)
Relative acceleration: A(x, y) is the acceleration of x with respect to y, where y is something traveling on a geodesic
Changes in these relations involve changes in the terms. You cannot have the terms remain identical and have the relations change, so again there is no change in predicates per se. Changes in derivative properties (velocity, acceleration) can be (formally) caused by changes in place (relative position). These changes (in velocity or acceleration), however, are purely quantitative. There is no change qua quality or qua relation. Once more, relation is not a terminus of movement. This does not mean that relations cannot change accidentally (i.e., in intensity, in quantity, or as a result of a change in their terms or arguments).
Activity and passivity consider objects relationally as the changer or the changed. If we admit movement of activity, there could be change of change or movement of movement. Aristotle and Aquinas held that this is impossible, but they were looking at the problem with the concern that the primary movement would be indefinable and physically unexplainable if this were allowed.
Movement can move only accidentally. Local motion as such cannot be altered or locally moved, but only accidentally, via a mobile that is moved or altered. This is simply a consequence of the fact that relations as such do not exist by themselves, but are ontologically dependent on the accidents or substances of which they are predicated, i.e., their terms, arguments or subjects.
Aristotle gives four arguments against movements of movement. First:
So, if there is to be movement of movement, that which is changing from health to sickness must simultaneously be changing from this very change to another. It is clear, then, that by the time that it has become sick, it must also have changed to whatever may be the other change concerned (for that it should be at rest, though logically possible, is excluded by the theory). Moreover this other can never be any casual change, but must be a change from something definite to some other definite thing. So in this case it must be the opposite change, viz. convalescence. It is only accidentally that there can be change of change, e.g. there is a change from remembering to forgetting only because the subject of this change changes at one time to knowledge, at another to ignorance. [IV, 2]
We can clarify this with formal symbolism. Let M(a, b) be the movement from terminus a to terminus b. Further, suppose there is some movement of movement, say N(M, M’), i.e., a movement from M to some other movement M’. So, by the time the subject of M has arrived at state b (or before then), it is now in some other movement M’. If N is a real physical movement, not some mere incidental or accidental change, then M’ should be a movement with respect to the same property defined by M. In that case, M’ has definite termini (a’, b’) corresponding to physical states of the same property instantiated by the termini (a, b) of M. If M is changing into M’, then this transition must take place sometime before (certainly no later than) the arrival at terminus b, or else there would no longer exist a movement M to be the terminus a quo of N. Any other movement M’ that is not M yet is of the same property would be moving toward some b’ that is not b. This b’ cannot be in the same direction as b, or else there would be no real change in movement (only a lengthening or shortening of the movement). Thus b’ must be in a different direction, so M’ is opposed to the first movement M.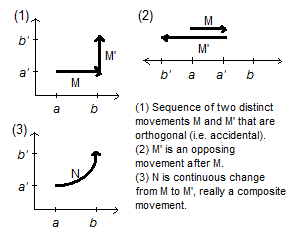 
This is not really movement of movement, but a sequence of movements, first going one way, then another. Note that the argument is not substantially affected if we suppose that we complete the movement
from M to M’ before M is completed. In that case, the movement M’ could be a continuation of M, rather than a contrary movement. [See diagram 2] This still would not really be a movement of movement. [See diagram 1] If we think of M transitioning to M’ via a continuum of intermediate movements, this is really nothing more than a continuous change of direction in phase space, not a movement of movement. [See diagram 3] Whatever the subject may be, movement is change from one form to another.
(IV, 2) Supposed movements of movements such as we have discussed are really composite movements, since a movement is defined by its termini.
A second argument is that if we allowed the movement itself to move (or change itself to change), there could be an infinite regress prior to its completion. Becoming X
could not occur because becoming
itself was in the process of becoming, and this process in turn was becoming, etc. If this sort of Zeno’s paradox were allowed, nothing can become or be moved or change.
(IV, 2) Aristotle is not assuming a static notion of being, but process. If we acknowledge that anything exists, even in flux, then we cannot have change itself be the subject of change. If there are to be changes of changes,
these cannot be ontologically or causally prior to the changes in question.
This is clear enough in the case of substantial generation or creation. Before some substance X can come to be, becoming
would have to come to be,
etc. This holds also for movements between predications a and b. The subject of movement, S, becomes b
in a predicative sense S is b.
Yet if there is some movement of movement, i.e., N(M’(a’, b’), M(a, b)), then S must move from M’ to M before it can become b.
Thirdly, if a thing is capable of any particular motion, it is also capable of the corresponding contrary motion or the corresponding coming to rest, and a thing that is capable of becoming is also capable of perishing: consequently, if there be becoming of becoming, that which is in process of becoming is in process of perishing at the very moment when it has reached the stage of becoming: since it cannot be in process of perishing when it is just beginning to become or after it has ceased to become: for that which is in process of perishing must be in existence. [IV, 2]
This argument from contrary changes can be expressed formally as follows. The contrary of movement M(a,b) is M(b, a). Any subject S of movement M can also in principle be a subject of M. We can generalize this to substantial perishing and creating by making a or b represent non-existence or nullity. Even in the predicative sense, however, we can speak of qualified becoming and ceasing to be (Sec. 15.1). When S moves from state a to state b, it is becoming b and ceasing to be a. Suppose there can be some movement of movement, N (M, M’). In movement M, S is becoming b and ceasing to be a, yet in movement M’ it is becoming b’ that is not b (though b and b’ are of the same property, or else we would have two distinct incidental changes, not change of change), and therefore ceasing to be b. Thus in moving
from M to M’ it is transitioning from becoming to b to ceasing to be b. This is to say M’ = M (or an extension or contraction of M).
A fourth argument uses the supposition that there must also be an underlying subject of change. If this were not so, i.e., if there were merely change
without something that changes, we would just be describing a mere succession of states, without some existent that is actually in those states. This would not be real physical change, but just a formal graph or locus of points in phase space. It makes no sense to speak of change or becoming
(absolutely or predicatively) unless there is something becoming. Once we admit that real physical change requires a subject that changes (this need not be a substance), then we may admit a fourth argument against change of change. Again, this is clearest in the case of simple becoming or genesis. The becoming of X
cannot be X, since that would require us to posit X before it exists. If X is a movement, then the becoming of X
cannot be that movement. If X is becoming,
then becoming of X cannot itself be a becoming, which is a contradiction. Yet all movement involves either absolute or predicative becoming, so there cannot be becoming of X
where X is any movement.
If, instead of generation, we consider qualitative or local movement, then movement of movement would require the subject and the terminus ad quem (eis a kinountai, what it moves to
) to be alteration or local motion. We would have to say that alteration can be locally moved or altered, or that local motion can be altered or locally moved.
Although it is impossible for movement to move, we should keep in mind that movement itself is a kind of relation, and in general we can have relations of relations without contradiction. If we restrict our consideration of movements to their generic relational aspect, we may define movements of relations, i.e., continuous changes in relative physical attributes, but not movements of movements.
It is uncontroversial that there can be movement in place, since this is our model for all other kinds of movement. Newtonian mechanics, however, also seems to admit movements of movements,
though in a different sense from those refuted by Aristotle and his commentators. These can be expressed as derivatives of the function of position. Velocity is a change in position with respect to time, and acceleration is a change of velocity with respect to time. Although it is convenient to treat velocity as a quality of movement that varies over time, in reality it is entirely derivative of successive displacements of position. In other words, if we have the locations and times of every point on an object’s trajectory, we have already specified the velocity, the acceleration, and all higher-order derivatives by implication. There is no infinite regress, since we do not need the higher-order derivatives to account for the movement in place. Nonetheless, the derivatives of motion, especially velocity and acceleration, do have important physical significance, to the point that we would consider our account of a motion to be incomplete without them.
Velocity and acceleration are not ontologically prior to the place and time of their subject, but derivative of these. On the other hand, we recognize the magnitude of velocity and acceleration as reflecting the strength of the force or impetus that causes movement. Yet it would be a mistake to say that velocity causes a change in position, or that acceleration causes a change in velocity. If we allowed that, you could have an infinite regress of derivatives, and never arrive at a completed movement.
Such derivatives are not examples of change being the subject of movement. A positive acceleration is not a moving movement, but a variation in the degree (velocity) of movement from one time interval to the next. Derivatives of motion can be defined with respect to a trajectory, without regard for it as representing a process that occurs to a subject. Rather, derivatives are features of the trajectory. Thus there is only one and the same subject and one and the same movement. There is not one subject that moves at some velocity and another subject that accelerates, nor is there one movement that has velocity and another that has acceleration.
Quantity may be predicated simply of substance, telling us how much substance there is. Aristotelians and Cartesians measured the quantity of substance by its volume, but modern physicists use mass or number of particles. Quantity may also modify other accidents, namely qualities and relations.[7] We generally understand quantity to be an extensive magnitude, i.e., a discrete number or continuous measure. Even if there are no actual contraries in quantity, there is contrariety between quantitative increase and decrease, since these tend toward opposing extrema, definite (e.g., zero) or indefinite (plus or minus infinity). Thus quantities can be termini of physical movement, not as dimensionless numbers, but as measures of some substance, quality or relation.
Quality, which defines a kind or likeness among substances (Categoriae, 8), admits movement, called alteration, not only between two actual contraries as termini, but also between more or less of a particular quality. As noted, quantity (extensive magnitude) may modify quality, but more generally we find that qualities may vary by intensive magnitude, which is ordered into greater and lesser, yet without a definite unit of measure. Intensive or extensive magnitude of quality is generally called the degree or intensity of a quality.
Some qualities do not vary by degree, in which case transition from one to another is possible only by continuous movement in some underlying quantity of another quality, relation or substance. This is what is meant by a change of degree (in an underlying quality) effecting a change in kind.
A movement in degree, as such, is not really alteration, for what is changing is the magnitude of a quality, though this may also effect a change between qualities. If the magnitude is extensive, this is really a movement in quantity. Intensive magnitude, degree in the classical sense, was traditionally placed under the category of quality, but it may well be that all intensive magnitudes are the result of some underlying quantity whose unit of extensive measure we do not know. Modern physicists proceed on the assumption that all physical properties have extensive magnitude or quantity, or else are discrete states that result from changes in underlying quantity.
A movement in degree of a single quality has as its contraries the fullness of that quality (some definite or indefinite degree) and its utter privation or absence. This seems to depart from our usual conception of movement as between two positive existents.[8] Since we are dealing with accidents, however, it is always presupposed that there is some underlying subject that has or lacks the quality in question, so neither of the termini is absolute nothingness. The same holds for when one of the termini of quantity is zero, which would be problematic only if quantity is predicated simply of substance, giving us absolute creation or destruction, both of which are incompatible with physical movement. (There is no contradiction if one existent perishes by generating another.)
Relations can indirectly admit of degree by being predicated of qualities that do so. Just as a single substance can receive contrary qualities and relations over time, so can a single quality varying by degree admit contrary relations.
Contrary qualities cannot inhere in the same substance unless they differ in time, respect (quantity or degree), or relation. Contrary relations cannot be predicated of the same subjects unless they differ in time. (The arguments or variables of a relation are not predicated of the relation itself, but of the subject of the relation.)
Time is the only other category predicable of relation. Time may modify relation extrinsically, or by incorporating time-dependent variation into the definition of the relation. In the latter case, the relation does not change into something other than itself, since the time variation is built in. Nonetheless, it defines real movements between relational forms over time. This time-varying relation may itself be considered a movement.
There could be change as the subject of movement as one process is replaced by another; i.e., changing from falling ill to becoming well, but such change is accidental, because movement is change from one form to another. So when you supposedly move between movements, what is really going on more fundamentally is that you are moving toward the terminus of the second movement rather than that of the first. That terminus will be in one of the allowable categories of movement (quantity, quality, place, relation), so that the apparent movement of movements is fully reducible to this other category.
It is conceivable for such accidental changes between movements to change categories, i.e., going from a qualitative movement to a local movement. Since this is merely an accidental or incidental change, this is not a physical movement. Rather one kind of movement has ceased and another has begun. The categorical distinction would seem to preclude a continuous transition, unless we say the magnitude of one movement per unit time diminishes while the other increases. Still, the terminus ad quem of each movement is categorically distinct, so we have two distinct movements, not a movement of movements. Alteration does not become local motion; rather alteration diminishes and local motion arises, perhaps by a common physical cause, but the alteration as such does not become movement. All of this applies only to cases where the relation between the alteration and the local motion is purely incidental or accidental, not natural.
On the other hand, there can be cases when qualitative alteration and local motion are physically linked. In fact, Aquinas held that all qualitative alteration was ultimately caused by local motion, and such is the consensus of modern physicists, so that the study of qualities is deemed superfluous in physics. When local motion effects a qualitative change, however, this does not mean that alteration as such has moved in space, nor that motion as such has changed in quality.
Peter of Auvergne objected that if local motion causes one quality (e.g., heat), it must also be the cause of the contrary quality (e.g., cold). It is impossible for the same thing to be the formal cause of two contraries. The reduction of macro-properties to the local motions of ensembles of particles (e.g., pressure, temperature) would seem to make local motion a formal cause of these properties. It is not an efficient cause, since pressure and temperature are not posterior effects of constituent motion, but effectively identical with it. We avoid contradiction because the so-called contraries are really relative or absolute privations of the characteristic motion defining the property. Insofar as there really are contrary qualities, e.g., our sensations of hot and cold, these are determined by distinct kinds of movements (neural activities).
While alteration does not move locally, it might be possible for local motion to change in quality. Historically, velocity was regarded as a quality, not only by the late Scholastics, but also by Galileo. This notion of speed (since velocity
was non-vectorial) as a quality is intuitive enough, as we may consider one animal to be faster than another, making speed
an inherent property of a substance. Note, however, that the speed was a property of the substance, not of its motion. Speed (in a given frame of reference) may help us determine what kind of a thing something is, as an object may have different physical characteristics based on its kinetic energy.
Velocity, acceleration, and other kinematic derivatives are all completely determined by the formal structure of a motion, i.e., the trajectory, a parameterized locus or distribution of locations over time. Thus it might be meaningful to think of these derivatives as qualities or properties of a motion, without immediate reference to the substance moved. They must still be ultimately referable to the subject of motion, for how can there be velocity
without something moving? An advantage of predicating these qualities of the motion rather than the substance is that it lets us regard them as extrinsic accidents rather than things that inhere in a substance. Descartes first advanced in this direction, by regarding kinematic properties as relative differences
among bodies, rather than something inhering in them. We cannot speak of body A moving away from B without B also moving away from A.
This account of kinematic qualities
would seem to allow that a local motion can change in quality. For example, the velocity of a motion can be higher in one time interval than in another. This would not change the kind of motion, however, but only its degree. Although velocity
is a quality of motion, changes in velocity are not alterations in the sense of one quality being replaced by another, but only in the sense of a quality varying in degree. Further, if velocity is an extrinsic accident that can only be defined relationally, then the form of the moving subject is unchanged by a change in velocity. Only the form of a relation between two or more objects is changed. This relation does not change in kind from a mere change in velocity as such, so again we have only a change in degree or magnitude.
Changes in the degree of a quality are really changes in the category of quantity (how much
) rather than of quality (what kind
). A thing (substance, quality or relation) does not become an other
(alter) by a change in degree per se, so it is not alteration, though there may be cases where a change in degree effects a change in kind, e.g., phase transitions. Thus changes in velocity, acceleration, etc. as such are quantitative, not qualitative, changes, even though velocity, acceleration, etc. are qualities. This agrees with modern quantitative treatments of derivatives of motion while still respecting classical ontological insights.
While it is credible that velocity and acceleration are physical qualities, it seems problematic to grant similar status to all the derivatives of motion, since that would require positing an infinity of existents for an infinitely differentiable function (e.g., a sinusoid). We should have to distinguish mathematical form from physical form. Only the latter can be a principle of change. In the modern understanding of physics, it is the second derivative, acceleration, that corresponds to the magnitude of force. Higher derivatives are real in the sense that they are accurate mathematical descriptions of the structure of a motion, but they do not act as physical qualities. The third derivative or jerk
is experienced as a change in force, yet it is only force that we feel. The higher derivatives do not represent forces of forces, even though the fourth derivative is the second derivative of acceleration. Otherwise, we would have the same problem of infinite regress protested by Aristotle and Aquinas.
How shall we distinguish whether movements are physically distinct in kind or whether they are distinct in number (as opposed to one being a continuation of another)? First, it should be evident that specifying the termini of a movement does not always suffice to specify the physical kind of movement or to define a physical unit of movement. For example, we can have inertial rectilinear local motion from point A to point B, but this is not the same kind of movement as moving orbitally in a semicircle between the same points A and B. Some physical movements, to be sure, are path-independent, such as changes in potential or applications of conservative forces. Regardless of path-dependence, knowing that two movements share a common terminus may not suffice to determine whether they are physically distinct or merely continuations of another.
Aristotle finds that three things are needed to determine the species and unity of a movement: the mobile subject (which persists throughout the movement), that in which it moves (the place, quantity or quality that changes), and time. Here time is considered distinct from movement, in agreement with Aquinas’ view that it is an extrinsic measure of movement. We have seen that there is no obstacle to admitting movement in the category of substance (Sec. 15.6.1), and that we can admit movements in relation only accidentally, i.e., insofar as they are relative movements in quantity, quality or location. (Sec. 15.6.2)
Of these three it is the thing in which the motion takes place that makes it one generically or specifically, it is the thing moved that makes the motion one in subject, and it is the time that makes it consecutive: but it is the three together that make it one without qualification: to effect this, that in which the motion takes place (the species) must be one and incapable of subdivision, that during which it takes place (the time) must be one and unintermittent, and that which is in motion must be one—not in an accidental sense (i.e. it must be one as the white that blackens is one or Coriscus who walks is one, not in the accidental sense in which Coriscus and white may be one), nor merely in virtue of community of nature (for there might be a case of two men being restored to health at the same time in the same way, e.g. from inflammation of the eye, yet this motion is not really one, but only specifically one). [Aristotle, Physics, V, 4]
If we have the same kind of displacement, or the same kind of quality, or the same kind of quantity changing, then movement is of the same species or kind. For a movement to be absolutely (i.e., numerically) one, it must also be changing with respect to something incapable of subdivision. Contrary to Aristotelian and Scholastic belief that species of physical objects and properties are usually defined by discrete forms, there are in fact precious few things in physics that meet this criterion. Among these, perhaps, are the quality of electric charge and the substantial forms of fundamental particle states (e.g., being an electron neutrino or a muon neutrino). Aristotle thought that color was such, and Aquinas thought that position or situs was such (apparently basing his notion of position on Aristotle’s more limited, discrete examples (sitting, lying) given in the Categories). At any rate, the species of movement is merely the species of the substance, quantity, quality or place that constitutes the states being traversed. This seems clear enough for substance and quality. For quantity, the relevant species would be that of the quality or substance being increased or decreased qualitatively.
For local motion, however, it is not immediately clear how, if at all, we should make distinctions in kind. Since there is no absolute place or direction that is physically relevant, we can make no meaningful distinction between upward and downward movement. Considering local motion in itself, without regard for which kind of physical force is its cause, we may distinguish linear and rotational motion as irreducibly distinct. Within each category, we may distinguish inertial and non-inertial motion. Inertial motion is a change in relative linear or angular position, with fixed linear or angular momentum in a given frame. Non-inertial motion involves changes in linear or angular momentum, i.e., acceleration. It is physically meaningful to further distinguish accelerated motion, between freefall trajectories along spacetime geodesics and deviations from such geodesics by application of a physical force.
For something to be a single physical movement, it must be of the same species. Movements in two different properties should be considered two physically distinct movements, even if they are simultaneous, though this distinction need not deny any causal linkage. Further, a single movement must always have the same subject. If first one thing moves and then another thing moves, this is hardly the same movement even if the property is the same. Again, this does not deny a continuity in physical causality.
How should transfers of momentum be regarded? After all, when one billiard ball transfers its momentum to another, there are two different subjects of movement, yet we are dealing with the same momentum, which may be regarded as a quantity of motion. Nonetheless, elastic collisions and other interactions introduce some discontinuity, as is clear from cases with changes in direction or total velocity (due to inequality of mass). There is no contradiction in allowing that the same momentum is present in multiple motions, any more than allowing that the same energy does different works.
Lastly, for a movement to be one, its time or duration must be an unintermittent unity. Obviously, if there were a gap or delay between two periods of movement, this could not be a single movement. What about transitions between states without intermediaries? These would seem to be instantaneous, which is incompatible with some continuous duration of movement. Quantum mechanics provides a solution, by allowing for a continuously evolving time-dependent wavefunction between measurements, during which neither discrete state is actualized.
Unity in time seems to require only continuity, not some specific unit or amount of time. We cannot look merely to time elapsed in order to determine when one movement has ended and another has begun. This leaves unresolved how to determine whether the same movement continuously repeated in the same subject should be considered a single movement or many. For example, when an atom vibrates in a lattice or a planet orbits its sun, should each oscillation or revolution be considered a distinct movement, or all the repeated cycles a single physical movement?
At this point, we might ask whether such a distinction really matters, or why we should bother at all about defining a unity of movement. Since we are considering movement as a real physical entity, it is incumbent upon us that we discern it as a distinct object of study. We are not talking about merely formal unity or multiplicity, but physical unity or multiplicity.
On that basis, it would seem that repeated oscillations or revolutions should all be considered a single movement unless they are altered in some way. We note that the same body can have multiple movements, as a planet has its diurnal rotation, its revolution about the sun, orbital precession, and various perturbations that may effectively slow or accelerate its net linear and angular motion.
For simplicity, we consider each movement in isolation, and ask how it can be ended in time if time and movements are always continuous. That is to say, the world and its contents are in constant flux, so it seems arbitrary to mark a point in time where one movement ends and another begins. The only physical justification for such distinction would be an interruption or discontinuity in the magnitude, rate or direction of movement. Examples of events causing such discontinuity include collision, reflection, emission, and absorption. Refraction by an abrupt change in medium would also seem to introduce discontinuity, but it is also possible to have gradual, more or less continuous refraction in a medium with a temperature gradient.
Aristotle amplifies that two durations of movement form a continuous unity when their endpoints are connected, without interruption by a period of rest. By this standard, even a reflected photon might be considered still in a single local motion, so it is always in the same movement throughout its life in a vacuum, which comports well with its timelessness.
A discontinuity in its direction is accounted not as making two motions, but a single irregular
motion.
Nonetheless, reflection does introduce a discontinuity in the first derivative, since there is no single velocity (i.e., speed with direction) at that point. Reflection may in fact be considered a non-trivial physical interaction, as shown by its dependence on surface orientation, so that only the vertical component of flux is reflected. This is incompatible with the point-like model of the photon, and requires us to consider it having some spread to interact with multiple atoms. Indeed, reflection becomes diffraction when the boundary is much longer than the wavelength, suggesting that reflection itself may be a wave phenomenon.
The distinction between regular
and irregular
applies primarily to local motion, though it may also be applied analogically to any movement that can be represented geometrically.
A regular motion is such that any part of its path may be applied anywhere else on the path; e.g., linear and circular motion. Otherwise it is an irregular motion, which can be represented as a broken line (e.g., reflections), a spiral or other non-repeated path.
Aristotle understands path
to also specify speed at that point on the path, so regularity of motion entails a regularity of both locus and speed. While this could theoretically be achieved by cyclical variations in speed, he takes it for granted that a regular motion must always be uniform in speed, since a change in speed would interrupt or alter the motion.
In any event, this definition of regular motion corresponds nicely with the modern physical concept of uniform motion. This includes not only motion in a straight line or in a circle, but also simple harmonic oscillations or vibrations, which have a constant angular frequency or angular speed. Succinctly, we define uniform motion as traveling an equal distance in an equal amount of time, which implies constant speed, though not constant velocity.
Aristotle assumed that the intrinsic motion of a natural body must be regular, so that irregularity of motion implies some extrinsic interference. This explains why later Aristotelians objected to the elliptical motion of the earth. Early heliocentrists, for their part, wrongly supposed that the motions of the planets were intrinsic. As we now know, they are in fact the result of an external force law. (Gravity can be understood as an extrinsic force between distant bodies, though at a deeper level, it may reflect the interaction between mass and space.) Thus the basic insight that non-uniformity of motion implies some extrinsic application of force still holds even under Newtonian mechanics. Uniform circular motion, however, is not intrinsic to any body except as part of a rigid body rotation.
In modern physics, we can define regular motion in a more general sense, without requiring constant speed. Instead, a motion is regular if its trajectory is on some smooth submanifold of the position-momentum phase space and is periodic. By this standard, the elliptical revolutions of the planets in their orbits are regular motions, notwithstanding the fact that the planets vary in speed. This is a useful distinction from the unpredictable chaotic motion that can arise in non-linear systems. In such systems, there is not always a sharp distinction between regular and irregular motion, but more or less regular motions can sometimes arise as stable states.
This broader concept of regular motion opens the possibility of defining regularity across changes in a plurality of properties, even of different categories. Aquinas thought that local motion followed by qualitative alteration could not constitute a single continuous movement, even if they are continuous in time. Continuity of movement requires the extremities to be one, which is hardly the case when one extremity is a place and another is a quality, even if they are simultaneous. [Commentary on Physics, 704] This is true enough if the first movement is purely local and the second is purely qualitative, but if we construct a phase space with both variables, it is conceivable that both properties may vary continuously in a way that traces a smooth continuous trajectory in phase space, in which case we might call such movement regular if it is periodic.
[1] It remains to be seen if substances can be termini. See Sec. 15.6.
[2] This broader, novel definition of contrariety is different from the classical definition followed in the Introduction to Ontological Categories, VI. In the old definition, quantities cannot be contraries. Strictly speaking, this remains true, since there is no definite quantity corresponding to the extremes of positive and negative infinity. Still, the contrariety of direction (which is, strictly speaking, qualitative or relative, not in the category of quantity) provides a basis for applying the notion of contrary to quantity.
[3] This should not be confused with relations
as defined in set theory. A relation R is defined as a set such that any member z of R is identical to an ordered sequence of elements (x1, x2… xn). Depending on the number of arguments n, we call this an n-ary relation (binary, trinary, etc.). This purely set theoretic definition does not really give us a relation in the ontological sense, but only a set of possible values for arguments. An ontological relation is only implicit in the structure or pattern of the n-tuples allowed.
A function is a particular kind of relation (in the set theoretic sense) such that every set of arguments corresponds to exactly one element in R. In other words, a given z = (x, y), but cannot equal any other ordered pair. This corresponds with our ordinary algebraic understanding of a function, having exactly one output for each input.
A predicate is a characteristic function of a relation; i.e., a function that gives a value of 1 if the proposition is true; 0 if the statement is false. For a simple one-place predicate, the statement P(x) is true if x is P
and false if x is not P.
An interpretation of a predicate is a function that takes values of its arguments as inputs and produces 1 or 0 (true or false) as its output. It is a function because every set of inputs produces exactly one output.
Say P(u, v) is true when u < v. An interpretation of predicate P is the relation consisting of all pairs (u, v) such that u < v. For any element z of P, z = (u, v).
[4] See note 3.
[5] George Henry Lewes. Problems of Life and Mind (1875), Vol. 2, p.128.
[6] K. Tahir Shah and W. Yourgrau. On Some Aspects of the Logico-Mathematical Foundations in Physical Theories
(IAEA, Miramare - Treeste, Aug. 1978). A functor maps a mathematical structure to some physical model. In general, a mathematical structure does not uniquely specify a physical model, so there can be a plurality of functors from the same structure onto different models.
[7] Quantity may also modify space and time, but these are not subjects of movement, so they do not concern us here.
[8] C.P. Long thinks that Aristotle himself equivocates on this point in Physics I, 7, offering two accounts of movement: a three-term model with a subject and two contraries (Sec. 15.1), and a two-term model with the subject (hypokeimenon) interpreted as matter and a single antikeimenon interpreted as a privation (steresis) of form. In fact, Aristotle considers the presence of the form no less essential than the privation. Further, the hypokeimenon is not absolutely formless matter, but only lacking the form that it will receive as movement is completed. The privation is best interpreted as a member of the complement set to the form in question. [Christopher P. Long. The Ethics of Ontology p.37.
© 2015-17 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
| Home | Top |