[Full Table of Contents]
16. Opposition to Movement
16.1 Contrary Movements
16.2 Rest Opposing Movement
16.3 Rest Opposing Generation and Destruction
16.4 Immobility
16.5 Relativity of Rest and Movement
17. Natural and Violent Motion
17.1 Acceleration and Deceleration as Violent Motion
17.2 Force and Acceleration under Relativity
17.3 Circular or Rotational Motion as Natural or Violent
17.4 Non-Violence of Movement in Quality and Quantity
18. Simple Motion
There are different senses in which a movement might be opposed or counteracted. First, there could be another movement that is contrary to the movement in question. Second, the subject of movement may have an intrinsic tendency toward a state of rest or a resistance to movement. Third, an external agent may impose a new movement on a substance, causing it to digress from the path of its intrinsic movement. We will evaluate each of these situations in terms of the concepts discussed in the last chapter, and see how they may be applied to classical or relativistic mechanics.
The notion of contrariety of movements holds importance even in modern physics, where we speak of an opposite motion or action, and in chemistry and biology, where we can speak of a reverse process. Aristotle finds five logically conceivable kinds of contrariety in movement.
The first kind of contrariety does not tell us the direction of incoming and outgoing movement, so it is insufficient for specifying the contrariety of movements for systems of more than one dimension. It is suitable, however, for defining the opposition of generation and destruction, which are specified by only one positive terminus, the other being a privation of form. Generation and destruction, we have noted, are not movements per se, but only insofar as there are underlying continuous processes with positive termini. Generation and destruction of a substance may be considered contrary changes (not movements, which have two positive termini) by their respective approach and departure from the same terminus.
Aristotle rejects Option 2 for several reasons. First, leaving a state, by itself, tells us nothing about where a movement is headed, so we cannot be sure if the movements are really contrary. They might both be headed toward the same intermediate state as a terminus, in which case they have a common goal. (If they are merely passing through the intermediate state to the other contrary, then they could be truly contrary movements.) Secondly, moving away from a contrary suggests the removal of that contrary, so it hardly should be used to characterize the movement. Lastly, movement is best defined, on metaphysical grounds, by the state toward which it tends (i.e., its final form).
These objections are not insurmountable. In a one-dimensional system, an intermediate can serve as a surrogate for either extreme, thus serving as a contrary to the other extreme. For example, in movement from white to gray, gray is a surrogate for black, so it can be contrary to white. From this, we may gather that movements converging to an intermediate are truly opposite. Thus Aristotle’s first objection to #2 dissipates. While his second and third objections show it may be conceptually inapt, in fact any movements with contrariety #2 will be truly opposite.
The unsuitability of #4 is obvious, since, e.g., becoming less healthy is not physically contrary to becoming more sick.
Options 3 and 5 might seem to mean the same thing, but recall that change is not the same as movement. A movement, for Aristotle, must have two definite termini. So for two movements to be properly contrary, there must be contrariety in both termini, as in #5. Yet it would seem that Option 3 also defines a true opposition between movements, as becoming black
is opposed to becoming white.
Aristotle’s insistence on knowledge of both termini in order to determine contrariety seems too strong a condition. After all, a movement can be interrupted, yet we may still know it was opposite to another by discerning its trajectory. Also, we can have contrary changes even when there are no definite extremes. There is no definite extreme to up
or down
in modern cosmology, yet motions in these directions (defined in a given frame) are no less truly opposed, with no less real physical consequences.
Vector notation can indicate direction, hence contrariety, at each instant of a movement, without explicit knowledge of ultimate starting or end points. A vectorial direction implies knowledge of at least proximate states prior to and following the instant in question. Representing a time derivative (e.g., velocity) as a vector effectively analyzes movement on the basis of arbitrarily small segments of its duration.
As noted previously (Sec. 15.2), movement and rest are opposed by contradiction, not contrariety, for they indicate the presence or absence of continuous variation in some physical property or relation. Aristotle notes that a privation (steresis) is sometimes called a contrary (enantion), but we shall abstain from such equivocal usage, and consistently regard privative opposition as contradictory, not contrary. Aquinas, citing Metaphysics, X, notes that privation and possession are involved in all contraries, since one contrary entails privation of other. This only shows, however, that the contradiction of privation and possession is more general than contrariety.
Relativity has acclimated us to the idea that there is no absolute rest or local motion. In fact, we may be too accustomed to this idea, to the point of denying that rest and motion have any real physical distinction. Even under special relativity, however, rest has real physical significance, since we can only define an inertial frame with respect to some object defined to be at rest, either in that frame or some other inertial frame. Every inertial frame, at least in principle, can be the rest frame for some object. While rest is not univocal, it still has physical significance. So the following discussion should be understood in the context of the rest frame of some physical object, which is the only context in which the laws of physics have their intelligible forms.
Movement generally applies also to quality and quantity, so rest would mean remaining in some quality or quantity, without being in the process of changing.
While recognizing that movement and rest in general are merely contradictory, Aristotle holds that a particular rest (i.e., of a certain object in a certain state) can be contrary to a particular movement. Not just any rest is opposed to any movement. For example, rest in the terminus ad quem of some movement would not be contrary to that movement, but rather its perfection and consummation. He proposes the following scheme of contrariety:
M1 = movement from A to B
R1 = resting at A
M2 = movement from B to A
R2 = resting at B
Claim 1: M1 is contrary to M2
Claim 2: R1 is contrary to M1
Claim 3: R2 is contrary to M2
Claim 4: R1 is contrary to R2
The first claim is the established definition of contrariety in movement by virtue of opposing directions between contrary termini (or intermediate termini tending toward contrary extrema). Claims 2 and 3, which are equivalent to each other, mistake contradiction for contrariety. Rest in A, as such, does not oppose movement 1. Rather, it may be (in some cases) the result of movement 1 effectively being opposed by a contrary movement 2. The notion that rest is brought about by a kind of resistance to movement is what leads Aristotle to formulate these particular rests and movements as contraries, though this is improper, as the state of rest as such is merely deprived of movement.
The fourth claim completes the square of opposition started by the first three. If R2 is the contrary of the contrary of M1, then it has the same end as M1, so R1, being the contrary of M1, is also contrary to the end of R2. There is a certain internal logic to this formulation, if we suppose that A and B are contraries, which further accounts for what made it appealing to Aristotle. We should expect the result that resting at A is a contrary extreme to resting in B. Using his example, remaining in good health (A) is contrary to remaining in bad health (B). Likewise, remaining in good health (R1: rest at A) is contrary to movement toward bad health (M1: from A to B).
This account breaks down once we accept that movements do not always have definite contrary extrema as termini. Place has no definite extreme in either direction, and quantity has no definite upper extreme. Where there is no definite extreme, there can be no actually realized state of rest at an extremum to serve as a contrary to movement. For example, local motion from x = 1 to x = 2 tends toward the indefinite extremum of infinity, but there is no definite position corresponding to infinity, hence no state of rest there. Since neither x = 2 nor any higher value of x can serve as an extremum, that terminus B cannot be a contrary, so remaining in B (R2) is not contrary to movement toward the other terminus A (M2). Where there is only an indefinite extremum, the only contrariety can be in opposition of direction (Claim 1).
Apart from cases of movement between definite contraries, rest may serve as a sort of contrary only insofar as it is conceived as manifesting a resistance to movement. Here it is not really the state of rest as such that opposes movement, but some inherent stability or inertia in a physical object. Aristotle, intentionally or not, implies the reality of inertia when he asserts that remaining in a location A opposes (antikeitai) local motion from A to B. This use of the verb rather than nouns (antikeimenon or enantion) seems to suggest active resistance. In light of modern mechanics, it is useful to distinguish rest from inertia, where rest is a state of not moving, while inertia is resistance to motion. We find, however, that inertia is not resistant to all motion, but only to acceleration.
Resistance to linear acceleration is measured by mass, and resistance to rotational or angular acceleration is measured by a moment of inertia. Yet both mass and moment of inertia make positive contributions to momentum:
p = mv, where p is linear momentum, m is mass, and v is linear velocity
L = Iω, where L is angular momentum, I is moment of inertia, and ω is angular velocity
p, v, L, ω are vectors, m is a scalar, and I is a (second-rank) tensor.
Operating on the assumption that mass is a surrogate for the quantity of substance (valid for materials composed of stable atoms), Newton regarded the product of mass and velocity as representing the total quantity of motion. Since angular velocity is the vector product of the radius of rotation and linear velocity, the quantity known as moment of inertia serves as the correlate of mass for angular momentum, as it measures the radial distribution of mass with respect to the axis of rotation. For this reason, the moment of inertia is sometimes called angular mass.
In a closed system, i.e., in the absence of applied external forces, there is no net change in linear momentum. The fact that applied force is required to change a system’s momentum may be interpreted as implying that, left to its own devices, a mechanical object or system of objects tends to remain in a state of constant momentum. We may regard such a state as inertial, or restful in a more generic sense. Indeed, under the principle of relativity, there is no distinction between an inertial state and a state of rest except for an arbitrary choice of coordinates.
Inertial motion in the strictest sense means constant linear velocity. Less properly, we may regard constant angular velocity as a kind of inertial motion (though vectorially it is accelerating), insofar as it can persist in perpetuity without application of external torque (vector product of the radius of rotation and applied force). This conservation of angular momentum is a distinct principle, not derivable from Newton’s laws.
Inertia as measured by mass resists linear acceleration by an external force. Similarly, the moment of inertia measures resistance to angular acceleration by an applied torque. This can be seen in Newton’s Second Law and its analogue for torque:
F = ma, where F is force and a is linear acceleration
τ = Iα, where τ is torque and α is angular acceleration
F, τ, a, α are vectors
Newton’s Second Law is primarily expressed as F = dp/dt, so these equations are effectively time derivatives of the previous pair.
For a given amount of applied force or torque (F, τ), you get less acceleration (a, α) the more inertia (m, I) there is. Inertia is not really an anti-force, but a sort of resistance, akin to Ohm’s law:
V = IR
where a given voltage (V) yields less current (I), i.e., charge per second, in proportion to resistance (R). Inertia is in units of force/acceleration. Inertia and acceleration resemble contraries insofar as more of one implies less of the other for a given quantity of force. Yet the classical notion of contraries does not really apply since inertia and force are dimensionally different. Indeed, they are not even of the same tensor rank.
In relativistic mechanics, the inertial quantity m is a function of velocity: m(v) = γm0, where m0 is the rest mass (i.e., when v = 0) and γ is the Lorentz factor (1 - v2⁄c2)-1/2. In other words, a massive object has greater inertia at higher speeds, making it more resistant to acceleration, and giving less velocity in proportion to momentum: p = γm0v.[1]
Since kinesis contributes to inertia, we should not be surprised to find an interdependence between mass and relativistic kinetic energy. This is given as:
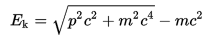
(Henceforth m is understood to be the rest mass.)
From this we define the quantity E2 = c2p2 + m2c4, where E, being the sum of the rest energy mc2 and the kinetic energy Ek, is called the energy
or total energy
of a particle, though it does not include potential. Since E = mc2γ is the energy of a free particle (i.e., with no potential), Ek = mc2(γ - 1). The relativistic kinetic energy then may be thought of as the amount of energy added to the rest energy by increased velocity, i.e., acceleration. We must keep in mind, however, that the quantity of kinetic energy is not absolute, since it depends on γ.
Since there is an inertia associated with energy (mc2γ), some textbooks speak of an inertia of energy.
This does not mean that energy as such is inert, but refers to the resistance to acceleration that increases with velocity. Nonetheless, what we naively have called the mass or inertia of a body is built up (at least in part) by positive contributions from the kinetic energy of its constituents. Internal attractive inverse-square forces make negative contributions to the mass, since these bring the system to a lower energy state.
Momentum and energy are interrelated as components of a four-vector: pμ = (iE/c, px, py, pz). This has a Lorentz-invariant norm: |p|2 - E2⁄c2 = -(mc)2.[2] The four-momentum pμ is conserved in a closed system, as are its components, namely the spatial linear momentum p and the energy E = mc2γ. This conservation applies even to inelastic collisions, implying that the relativistic kinetic energy Ek = E - mc2 is also conserved. When a moving particle has some or all of its energy absorbed by its target, this energy is converted into effective mass. Such inelastic collisions can be reinterpreted as conversions between kinesis and inertia, more commonly expressed as mass-energy equivalence.
So much for the opposition of local motion and rest. What of so-called generation and destruction? These are not movements, but changes whose termini are contradictories, not contraries. Is there a rest or inertia that may be considered an opposition or resistance to such change?
(1) Generation: change from not-A to A
(2) Destruction: change from A to not-A
Change #1 seems opposed to Change #2 in a manner analogous to contrary movements, but they each have a terminus that is merely a privation, so they need not be going in opposite directions if the generation or destruction is not absolute. For example, something may go from red (not-green) to green, or from green to violet (not-green), but these are not contrary changes. If the generation or destruction is absolute, then not-A is nothingness, which is not a subject. So the opposition is between arriving at terminus A and departing from the same terminus. This is not the same kind of opposition as in contrary movements. (See Sec. 16.1, Option 1 vs. Option 5.)
We saw (in Sec. 16.2) that there is a sense in which movement can be opposed by rest, or more properly, resisted by inertia, rather than by another movement. Since generation and destruction are not movements, they might be opposed not by rest, but by changelessness or non-change (non mutatio). Should this be considered a privation, or a sort of permanence?
[#1] If there is some positively identifiable substantive, its changelessness in being would be contrary to its changelessness in nonbeing. [#2] But if there is no identifiable nonbeing, we may ask: what is it to which changelessness in being is contrary? [Physics, V, 230a; R. Hope trans.]
In the first case, we are not dealing with absolute generation or destruction, but with the coming into being or passing away of some accident or some instantiated substantial form in a substance. In this case we may regard remaining in being and remaining in non-being as positively existent contraries; e.g., a substance persisting with some predicable attribute or form P or the same substance persisting with some non-P. Yet these are not really contraries, but contradictories, except in the case where non-P is the contrary of P.
If we are dealing with absolute creation or destruction (case #2), then remaining in being, in this case simple existence, has no contrary, for remaining in non-existence
is not a physical state at all. Nor can the process of destruction be the contrary of remaining in existence, since destruction may begin with that state, and we can hardly say a process is opposed to its starting point.
If non-being is taken as having an implied subject, Aquinas holds that one non-change can be contrary to another non-change: For, since non-being has a subject, there is nothing to prevent that subject from persevering in non-being, which is the same as not changing.
[Commentary on Physics, 734] Here, however, this is not absolute non-change, but only with respect to some definite property of form P. Something may persevere in being non-P, yet while changing from one thing to another. Persisting in being non-P would be opposed to persisting in being P. This is not mere negation of change, since it entails positive persistence. Nonetheless, since P and non-P are contradictories, it seems inapt to characterize persistence in either state as contrary to the other.
Recall that the logic of contradictories and contraries is such that contrary predications cannot both be true, while contradictories moreover cannot both be false (excluded middle). In ontological terms, contraries cannot both be present, or one is present to the degree the other is absent, while contradictories cannot both be absent
(non-predicated) either. That which exists, yet neither persists in being P nor persists in being non-P, would have to be changing between P and non-P. Thus persisting in P and persisting in non-P might be considered contraries rather than contradictories if we consider these both to have the common characteristic of persisting, not changing. Yet this persistence is purely formal in the case of being non-P, since that may admit countless changes among various non-Ps in the same genus or property-class as P. Accordingly, this contrariety
has no physical significance, since remaining non-P does not imply persistence in any physical attribute. We should not say that remaining non-P
is some definite state opposing remaining P.
Persisting in a state, be it with the attribute P or non-P, is not the same as non-change. The latter means the simple absence of change, which may be asserted even when there is no subject. Such is the case with absolute generation, which begins with a non-subject as its first terminus. That non-subject cannot be regarded as positive persistence of some definite mode of being, though it is not change either. Thus we cannot posit such rest
in opposition to generation or destruction.
Since generation as such begins with a non-subject, Aristotle does not allow that one generative process could be opposed to another, but he does allow this for destruction. He considers that a destruction could be contrary to another destruction qualitatively, as passing away pleasantly is contrary to passing away painfully. Here, however, it is not the destructions as such that are opposed, but some set of positive qualities affixed to the process. The same cannot be done for absolute generation, since nothing can be attributed to a non-subject. It may be allowed, however, for non-absolute generation, presupposing some subject. Nonetheless, such processes are only incidentally contrary.
Our allowance of absolute generation does not contradict the more general causal principle that nothing comes out of nothing. For one thing, absolute generation does not imply ex nihilo creation, since we are merely abstracting the appearance of some substantial form or property from any underlying substance. Second, even ex nihilo creation would be no contradiction of this principle if the agent of such creation has prior existence.
Properly speaking, there are no physical persistences or non-changes that are contrary to generation or destruction. Nonetheless, in physics, most, possibly all, generations and destructions are the result of some underlying movement, which does admit contrariety against inertia or rest. We have seen, moreover, that persistence and non-change are distinct, and so we may apply this distinction to movement, helping us articulate different meanings of non-movement or immobility.
We may speak of a substance or its properties being immobile
(akineton) in at least three senses. First, there is that which is absolutely incapable of movement. Second, there is that which is extremely difficult to move. Third, there is that which is capable of movement, but not actually in movement at the moment. This last sense is what is meant by being at rest. [Physics, V, 226b]
Absolute incapacity to move would seem to be incompatible with the notion of physis as a principle of movement. After all, physics is the study of sensible change, and it seems that all physical change is referable on some level to movement, a continuous variation between two terminal states. Thus, if there exists an absolutely immobile thing, this would seem to be beyond the study of physics, or at best some metaphysical presupposition of physical science.
On the other hand, conceivably a substance might be absolutely immobile in some respects, but not others. For example, the charge of an electron never changes, though its mass-energy and velocity may change. More generally, we may regard conserved quantities as immobile. Thus the total momentum of a closed system is immobile, though it may be dynamically redistributed among components. While this is an unconventional use of the term, knowledge of such immobility conveys physical information.
The second meaning of immobile, namely that which is difficult to move, may seem to be an improper or equivocal use that we should discard. On the other hand, this sense captures an essential aspect of what we have called inertia, namely resistance to motion. If this resistance were absolute, there would be no need to quantify inertia. It is precisely because this resistance varies in magnitude that we can articulate inertial kinematics, using mass and moment of inertia as dynamic quantities.
The third meaning of immobile does not define an intrinsic property of a subject, but rather its state of rest. It would seem that rest is just a privation (steresis) of a given type of movement, but it can also be construed positively as persisting in that privative state, since a subject must be presumed in order to speak of rest. What we have called inertia may make an object tend toward this state of rest, or at least resist changes (accelerations) from its present state of motion.
The relativity of local motion implies that we can only define being at rest
with respect to a given reference frame. Fortunately, rest can be defined in an important class of frames known as inertial reference frames. For a Newtonian, this would mean any frame that was at rest or in uniform linear motion with respect to absolute space. For those who deny absolute space (or at least that it is knowable), inertial reference frames can only be defined with respect to each other, which raises a problem of circularity. How can we know that any such reference frames are truly inertial?
In fact, we cannot know, but only postulate that an inertial frame is one in which the law of inertia holds. This law, articulated by Galileo and Newton, is that, in the absence of external forces, a body at rest stays at rest and a body in motion continues in a straight line at constant velocity. Our terrestrial frame of reference is inertial to good approximation, if we treat gravity as an external force applied downward. The diurnal rotation of the earth contributes a centripetal acceleration of only 0.034 m/s2 (at the Equator), much smaller than gravitational acceleration (9.8 m/s2 at the Earth’s surface), and other accelerations are even smaller.
Once we have one inertial frame defined, we can define countless others that are in uniform linear motion with respect to the first. There is no way to distinguish which of these frames is at rest with respect to absolute space, if such a thing exists. Their physical significance is that, in any such frame, an object at rest or in uniform linear motion will remain in that state with the same velocity. This implies that there is no absolute physical distinction between an object at rest or an object in uniform linear motion (though there could be a metaphysical distinction), as this depends on the choice of reference frame. Kinematic interactions are determined solely by the relative velocity of objects; it does not matter whether one or the other is really at rest. Thus, when speaking of local motion, we should understand rest more broadly as including linear uniform motion, i.e. all inertial states.
This more expansive notion of rest, where immobility and uniform linear motion are physically equivalent, was not recognized by the ancients, since all terrestrial motions are limited by drag or friction. The law of inertia implies that the absolute magnitude of motion (measured by velocity or momentum) is a matter of choice of reference frame. Nonetheless, the total amount of motion (as measured by momentum) remains constant unless an external force acts upon the system. This implies that force corresponds to a change in momentum or velocity, i.e. acceleration. A mere change in position requires no addition of motion (momentum).
Inertial reference frames are also important in special relativity, which postulates that relations among physical quantities, i.e., the laws of mechanics and electrodynamics, have the same form in all such frames. The difference from classical mechanics is that transformations of physical quantities between such frames are Lorentzian rather than Galilean, though the latter is a fair approximation for velocities well below c.
The law of inertia (Newton’s First Law) does not hold in frames of reference that are accelerating (with respect to an inertial frame). Acceleration is not simply a matter of choice of frame, for only the accelerated object experiences the push or pull of force. Strictly speaking, the rest frame of any massive object is accelerating, since all masses are subject to gravitational acceleration. General relativity lets us deal with accelerating frames by comparison with geodesic trajectories or freefall acceleration as a reference point. If gravitational acceleration is attributed to the geometry of spacetime, freefall trajectories effectively assume the role of straight line paths
and might be considered a more generic class of inertial states, at least in the sense of being intrinsic motion, not the result of an external applied force.
Applying the three senses of immobility or akineton (Sec. 16.4), we find that what is absolutely immobile (the first sense) is the conserved quantity of linear (or angular) momentum. This quantity is not absolute in value, but depends on the choice of frame. The second sense, what is difficult to move, inertia, should be interpreted as resistance to acceleration. In Newtonian mechanics, mass is a resistance to any acceleration. Special relativity shows that this resistance increases at higher velocity (which depends on choice of frame). General relativity, at least in the conventional interpretation, attributes gravitational acceleration to the effect of mass on the geometry of spacetime. Instead of making mass the direct agent of acceleration (which would be paradoxical if it is the measure of inertia), we might consider freefall acceleration as a geodesic trajectory favored by inertia in curved spacetime. Thus inertia is resistance to non-gravitational or proper
acceleration.
The third sense of immobility, a state of rest, is not absolutely definable in any theory of modern physics. In Galilean and Newtonian relativity, all uniform linear motion is equivalent to rest. This remains true for massive bodies under special relativity, but photons in a vacuum move at speed c in every reference frame, so they can never have a rest frame
where their speed is zero. In general relativity, inertial reference frames are theoretically possible, and experimentally observable to good approximation (i.e. a billiard table with surface orthogonal to Earth’s gravitational pull). Nonetheless, in fact all massive objects are accelerating gravitationally, so nothing is at rest
in the Newtonian or Galilean sense.
What we have instead, for any closed system, or for the universe as a whole, is a constant quantity of motion (momentum), though the absolute value of this quantity is arbitrary, depending on choice of reference frame. For a given frame of reference, nonetheless, the value of momentum is defined unequivocally.[3]
What can be said about the relativity of other types of movement besides local motion? Is increase or decrease in substantial quantity relative, or is there absolute size
? If the quantity of substance is measured by volume, as was done by the Aristotelians, Scholastics and Cartesians, then this is subject to the relativity of spatial length under special relativity. There would be a maximal proper
volume in the rest frame. If quantity is measured by mass, this too is relative, though there is a minimal quantity, the rest mass. Nonetheless, quantitative movement so defined is not purely relative, since a change in mass or volume in one reference frame will also be found in every other frame, though the magnitude of this change depends on choice of frame. If we measure quantity by number of particles, then quantity is altogether invariant.
Qualitative change might be relative insofar as quality depends on local motion. A field is electric or magnetic in quality depending on choice of frame. Some qualities, however, such as electric charge and quark color,
are altogether independent of reference frame. Such invariance allows us to speak of such qualitative states as being stable or at rest
for long periods of time. Thus the third kind of immobility may be admitted for qualities even under relativity.
The distinction between natural and violent local motion seems to have been adopted by Aristotle from an already existing way of speaking; it is not something he invented. The motion of a substance is natural if it follows from the nature (physis) of that substance, i.e., from an intrinsic propensity or principle of motion. Otherwise, the motion is violent,
i.e., the result of some extrinsic force that disrupts an object’s natural motive tendency.
Strong determinists hold that all motions follow from some natural necessity, so even violent motions are ultimately natural. Nonetheless, the distinction between natural and violent motion remains meaningful even in a deterministic paradigm, if we define them with respect to a particular substance under consideration. The natural
motion of a substance comes from the nature of that substance (i.e., its intrinsic properties), while violent
motion is the result of an external force, which causes a substance to deviate from its natural motion. Violence is not absolutely contra-natural, but only opposes the natural motive tendency of a particular substance. What is an external force to one subject may be intrinsically necessary to another subject.
The distinction between natural and violent motion is not to be confused with essential and accidental motion. (Sec. 15.3) While essence (ousia) and nature (physis) are practically equivalent here for Aristotle (since he supposes each ousia to have its own physis), accidental and violent motion are not the same thing. Accidental movement is not physically causal at all, but merely incidental. Violent motion, being the result of force, is clearly physical, though it is the result of an external cause, disturbing the motive tendency of an object’s internal motive principle or nature (physis).
With the above understanding, violent motion is only contrary to the nature of the substance being considered, not contrary to Nature
in general. This allows us to give a physical interpretation to contrariety. A state of motion or rest can be opposed to an object’s nature insofar as it is contrary to its natural motion, i.e., how it would move according to its intrinsic constitution.
In Newtonian mechanics, we do not consider an object to be motile in itself, except perhaps in inertial motion, which Newton attributed to a vis inertiae. Under the principle of relativity, inertial motion is indistinguishable from rest except by arbitrary choice of reference frame. Any deviation from this inertial motion or rest is attributed to an extrinsic force. We might see inertial motion as the natural motion of a massive object, with any acceleration from this state being violent motion. Yet we may also consider the motion of a stable system of bodies, like a solar system or an atomic system, treating the motions of its constituents as natural,
as contrasted with any violent perturbations or deviations imposed by outside forces.
While violent motion is necessarily the result of an external force, i.e., something extrinsic to an object’s natural principle of motion, it might not be the case that all motions resulting from external forces are violent in the sense of contra-natural. For example, if the nature of a charged particle is such that it is attracted to a particle of opposite charge, we might regard the resulting motion as natural.
In a physics where principles of motion are defined relationally, rather than as something inhering in each object, the distinction between natural and violent motion, or intrinsic and extrinsic motive principles, may be inapt. Instead, we might say that each object has an intrinsic propensity or inherent property (e.g., mass, charge) that causes it to move in a certain way depending on the presence of another object (particle or field). Both objects, however, are equally necessary for the motion, so we need not consider one or the other to be the sole originator, acting violently on the other.
Instead of using the contrast between natural and violent, we may interpret states of motion as results of balanced or unbalanced force (vis). When an object is under balanced forces, whose net sum is zero, that object remains in its state of rest or inertial motion per Newton’s First Law. Only when it is under unbalanced force, with a non-zero net sum, does it accelerate, deviating from the inertial state.
An important departure from Aristotelian physics is the emphasis on acceleration rather than velocity as the measure of physical action, as expressed in Newton’s Second Law, making acceleration proportionate to the net force applied. This implies, unintuitively, that no applied force is required to sustain constant velocity, a fact that was long obscured by the prevalence of gravity, friction, and air drag in terrestrial observations. Accordingly, Aristotle did not give acceleration the attention it deserves.
Aristotle does seem to discuss acceleration when he asks if any non-eternal state of rest is generated
by some process of coming to a standstill.
Here, however, he uses two arguments based on empirically false premises. In the first, he says objects move faster as they approach a state of rest. This might be true for objects falling to the ground, but not in general. The second argument invokes the erroneous notion of natural place,
to show that natural motion has a goal
of a state of natural rest.
Notwithstanding these errors, he has the insight that motion and coming to a standstill
are not different, except in conception. Indeed, we would agree that there is one motion which has velocity and acceleration, not an accelerating process that generates
motion at some velocity (or a state of rest) as though this were something physically distinct. If we took the latter tack, we could have an infinite regress of generation from higher-order derivatives of motion.
Still, we do recognize an important physical significance to acceleration, as a measure of force or violence (vis). In general relativity, however, gravitational acceleration is conceived not as an extrinsic force, but as the natural motion of a mass in a curved spacetime metric. Thus freefall acceleration would be considered a natural motion, as contrasted with proper acceleration, attributable to violence or force. Galileo considered the perfect uniformity of freefall acceleration as reason to regard this motion as natural, as contrasted with violent projectile motion.
Can the notion of violence ever be applied to states of rest? After all, it would seem that an accelerating object must be brought to rest violently by introducing an opposing force. Aquinas thought that objects could be brought to compulsory rest only per accidens, by lack of compulsory force. [Comm. on Phys., 747] That is, the violent motion peters out. This is an empirically erroneous explanation, but the insight that compulsory motion causes rest per accidens is sound. Aquinas recognizes that compulsory rest would be a problematic concept only if you deny that there is any coming to rest
(deceleration) in compulsory motion. In that case, no state of rest could ever be the direct result of compulsory motion. Yet compulsory motion can cause rest per accidens, though not in the manner Aquinas describes. Instead of the violent motion petering out, it imposes an acceleration that opposes a first motion, accidentally causing rest insofar as it is balanced by the first motion.
As a simple example of violent motion accidentally causing rest, consider a falling object striking the ground. The falling motion is a natural motion (both in general relativity and in Aristotelian physics, though for markedly different reasons), which is brought to a halt when striking the ground. We may explain this by attributing to the ground a normal force that opposes freefall acceleration. Both the gravitational and normal forces, considered in themselves, tend to accelerate an object, not bring it to a state of rest. Only when these forces are balanced does a state of rest arise. Hence it can be said to arise per accidens with respect to one or the other force. Neither the natural nor violent causes of accelerated motion are essentially productive of rest, though they frequently create such states when forces are in balanced opposition.
As noted previously (Sec. 15.8), Aristotle assumed that intrinsic or natural motions must be regular motions (i.e., linear or circular), which he understood to be uniform in speed. He considered freefall motions to be natural, yet he also recognized that the velocity of that which comes to a standstill seems always to increase,
apparently in reference to falling objects. Aquinas offers the metaphysical explanation that since each thing gets stronger and more intense as it gets closer to its perfection, it follows that the motion through which rest is produced is swifter the more it approaches rest, as is abundantly clear in natural motions.
[Comm. on Phys., 743] This inconsistency as to whether natural motion is uniform in speed can be resolved in one of two ways. First, we may restrict natural motion to inertial motion, and regard all accelerated motions, including gravitation, as the result of external force or violence, as in Newtonian mechanics. Alternatively, we may regard freefall acceleration as an intrinsic motion on a curved metric, as in general relativity, so natural motion corresponds to freefall gravitational motion, while violent motion is any departure from such motion caused by an applied force. So-called inertial motion is definable only in frames where gravitation is uniform to good approximation. If the gravitation is non-zero, we can only define inertial motion in the plane perpendicular to the direction of gravitational force.
For simplicity, let us begin with uniform linear motion. An external force causes a departure from this motion, and we measure the magnitude of this force by the change in momentum, which entails acceleration. The acceleration has the same direction as the force. Newton’s Second Law, F = ma = m(dv⁄dt) = dp⁄dt, indicates that the alteration of motion is proportional to the motive force impressed upon an object, and this alteration is in the direction that the force is impressed. To Newton, dp⁄dt is the alteration of motion, for momentum is a vectorial quantity of motion that effectively stands in for motion itself. Thus force in a given direction changes the quantity of motion in that direction.
In this formulation, the quantity of motion is changed only by violence. Yet this ignores Newton’s Third Law, that for every action, there is an equal and opposite reaction. Looking at the entire picture for any closed system, there is no net force, hence no net change in momentum. As a particular object is accelerated, it imposes an opposite force so the total system’s change in momentum is zero. We see increases in motion only as we choose to view an object in isolation, treating the source of its acceleration as something external.
Newton’s Third Law holds for contact forces even at relativistic speeds, as does the consequent conservation of momentum.[4] This means that the total quantity of motion, as defined in a given reference frame, can never increase or decrease. (The absolute value of the quantity of motion depends on the choice of frame.) Thus violent or forceful action does not add any total motion to the universe, but redistributes it among objects. It would seem, then, if we are discussing linear contact forces, that all the violent motion in the universe does not remove the cosmos from an inertial state as a whole. After all, if the total momentum of a system is always constant, this is indistinguishable from rest under a Galilean transformation.
We should note, however, that action-reaction symmetry would break down if we considered field interactions to be actions between separated particles. Since there is no univocal simultaneity at a distance, the supposed action and reaction between separated particles could not, in general, be made equal at every instant. It is only by considering a particle’s local interaction with a field that such symmetry can be maintained for every instant, and this only by positing that a field can somehow bear momentum. If we regard the field only as a construct describing remote particle interactions, then Newton’s Third Law and conservation of momentum do not hold for every instant, but only between the states before and after the duration of interaction. [See: A.P. French. Special Relativity (1966), pp. 224-25.]
Newton’s Second Law holds in its classic form only at small speeds. For speeds approaching c, we must, first of all, replace the mass m with the relativistic mass mγ. Thus the ratio of force to acceleration must depend on the choice of reference frame (since v is contained in γ). This oddity results from the fact that inertia or resistance to acceleration varies with speed, which in turn results from the fact that how much energy is inertial (mass-building) and how much is in motion with respect to externals depends on our choice of reference frame.
In special relativity, however, the relationship between force and acceleration is much more complicated than simply F = mγa. Force is Lorentz-invariant only longitudinally, i.e., along the direction of the vector v defining the relative velocity of two reference frames. Force applied in a direction transverse to v is not Lorentz-invariant. In both cases, the transformation of acceleration between frames is complex, though these simplify somewhat if one frame is a rest frame. The longitudinal acceleration in a moving frame decreases by γ3 with respect to the rest frame, and the transverse acceleration decreases by only γ2. This difference in ratios by component implies that the direction of force is not always the same as the direction of the acceleration it generates.
Although the magnitude and direction of acceleration depend on choice of inertial reference frame, it is not arbitrary which object is accelerating and which is not. There is a real distinction between acceleration and non-acceleration, regardless of frame, which follows from the physical reality of force. Although the magnitude of the transverse component of force depends on reference frame, the invariance of longitudinal force guarantees that there is no inertial frame in which the force can become zero. Only the transverse magnitude and therefore direction depend on the choice of frame.
Even this partial relativity of force seems difficult to make coherent. After all, a person or object under some force experiences some real push of definite magnitude. This is the force experienced in the proper frame, i.e., the frame accelerating with the observer. If we grant physical reality to the magnitude of force in this frame, as indeed we must if anything is physically real, we must again deny that there can be a single privileged frame. Rather, we can only know the magnitude of experienced force by considering the proper frames of each object undergoing violence.
While force in the proper frame is always some definite absolute quantity, force cannot be Lorentz-invariant, since it is a vector. In fact, it cannot undergo Lorentz transformation at all, i.e., it is not Lorentz-covariant, unless we generalize it as four-force, which is the derivative of four-momentum with respect to proper time, i.e., time along an object’s world-line. Since the fourth component of four-momentum is E/c, the four-force components may be written as:
Fx, Fy, Fz, (1⁄c)(dE⁄dt)
where Fi = dpi⁄dt, and t is understood to be proper time. The norm of the four-force is an invariant scalar, the square of which is:
Fx2 + Fy2 + Fz2 - (1⁄c2)(dE⁄dt)2
The timelike component consists of power (dE⁄dt) divided by c to give dimensions of force. Four-force may be thought of as expressing an interdependence of force as spatial gradient or as a change in energy, depending on choice of reference frame, reflecting the interdependence of space and time measurements. Alternatively, it is the relationship between force as change in kinematic momentum versus force as rate of change of energy transfer, reflecting the interdependence of energy and momentum in four-momentum.
This interdependence can be made more intuitive by considering the familiar example of electrical power (watts), which is equal to current times voltage, or charge/sec times potential/distance. Since current is a sort of velocity, it has the same relativity to reference frame. Accordingly, power will also increase or decrease proportionately with perceived current, for a given voltage. Put differently, the ratio of power to voltage will vary depending on choice of inertial frame.
Although F = ma does not hold in general under special relativity for 3-dimensional vectors and scalar mass, the fundamental form of Newton’s Second Law F = dp⁄dt does hold in a four-dimensional form for all inertial frames. Although we no longer have the classical relationship between force and acceleration, we still have force as a change in momentum. It is debatable, however, whether F = dp/dt is really a physical relation or just a definition.[5]
F = ma does hold if F is four-force and a is four-acceleration (the scalar magnitude of which is invariant), the derivative of four-velocity with respect to the proper time τ along a world-line. Four-velocity in turn is the derivative of four-position (x, y, z, ct) with respect to proper time.
Additionally, we can define the proper velocity as the ratio of the distance traveled to the proper time, effectively taking the spacelike components of the four-velocity. Proper acceleration and proper force are the 3-acceleration and net 3-force in the frame of the accelerated object, where the timelike components of four-acceleration and four-force are zero. Thus, the magnitude of 3-acceleration and 3-force in this frame is equal to the invariant scalar magnitude of four-acceleration and four-force, confirming that there is something special or real about force experienced in this frame. Vectorially, proper force is normal to proper velocity, which is momentum per unit mass. These proper
variables are all defined in a comoving frame, i.e., an inertial frame such that at some time t0 the accelerating object in question is at rest.
F0 = maγ3/γ⊥
F0 is proper force and γ⊥ is γ using the transverse velocity v⊥. For a fixed value of force Fo, as v approaches c, a becomes vanishingly small; i.e., force causes practically no more acceleration.
This discussion of four-forces and proper forces all pertains to special relativity (which is in fact capable of handling acceleration), yet these same constructs may also be applied in general relativity. There four-acceleration is treated as the covariant derivative of four-velocity, and a geodesic is a world-line of an object whose four-acceleration is zero. Such a non-accelerating
object would be considered in freefall or gravitational acceleration in a Newtonian paradigm. Under general relativity, however, gravitational dynamics are already built into the spacetime metric and stress-energy tensor, so gravity does not appear as an applied force or acceleration. The only contributions to four-acceleration are forces that cause deviations from gravitational freefall. Such contributions are sometimes called proper acceleration
in general relativity.
It may seem that the proper acceleration
of general relativity is at least formally different from that of special relativity (the derivative of four-velocity with respect to proper time), especially since the latter implicitly can include gravitational acceleration. Yet the proper acceleration in general relativity really is the full acceleration on that world-line, i.e., the covariant derivative of four-velocity over proper time. The nullification of gravity as an accelerating force is not a mere mathematical formalism, but a physical claim. The forceless state of freefall is corroborated experientially by the sense of weightlessness in space. On Earth, what people feel in freefall is not gravitation, but air resistance, followed by the normal force applied by the ground. Our sense of heaviness or weight while walking is the result of exerting force to oppose freefall tendency, keeping ourselves upright. Acceleration, unlike velocity, requires continuous application of force.
The Newtonian principle that all contact force is accompanied by an equal and opposite force holds in all frames, even accelerating frames. This implies that all such forces are interactive. Without the supposition of absolute motion, there is no way of saying which is the action and which is the reaction.
Not all interactions need to be modeled by contact forces, however. Force can be generated by distant objects moving with respect to each other, as in the case of charged particles varying in distance. In such cases, the principle of simultaneous action-reaction does not necessarily apply. When one source is stationary and the other moves in a given frame, we might attribute the resulting force to the moving source. Yet both sources are equally necessary, as is proved by transforming to another frame where the other source is the one at rest, or by considering a scenario when both sources initiate movement simultaneously. All known physical forces are relational, so their origin cannot be confined to one or the other object.
The reality of force or violence might be taken to imply that we can define absolute motion as that which is generated by force. Such a definition, however, could at most establish absolute acceleration, not absolute velocity or location, since we would have no way of knowing the true
initial velocity or location of the object subjected to an applied force. Also, Newton’s thought experiment of applying the same force to all bodies, yielding absolute motion for all without any relative motion between bodies, would hold only for some subset of bodies in the universe. For the set of all bodies in the universe, there can be no net external force without violating conservation of momentum. His reverse example, where you apply the same force to all bodies but one, yielding relative motion for that one body with respect to all others, even without force, is likewise problematic. We could certainly tell which bodies were truly accelerating because the law of inertia would not hold in an accelerating frame of reference. Anyway, this example once again supposes that you could apply a net external force to the set of all bodies in the universe. The reciprocal or relational nature of force makes such a supposition impossible.
Aristotle famously held that natural motions could be linear or circular, but under Newtonian physics, uniform circular motion is strangely treated as though an object were under a constant external force causing it to deviate from a straight-line path. Thus uniform circular motion, though regular, is not an intrinsic natural motion. The interpretation of uniform circular motion as forceful comes from the fact that direction is built into linear velocity, so a change in direction is considered an acceleration even if the speed remains the same. While there is no question of the mathematical rectitude of explaining uniform circular motion in terms of centripetal acceleration, it remains to be seen whether this is a formalism or the result of a real physical force.
For one thing, uniform motions, whether circular or more generally periodic, exhibit a smooth, rhythmic behavior that we would intuitively tend to regard as natural rather than violent. Violence, after all, is thought of as abrupt and discontinuous with previous motion, introducing an irregularity, though the violent motion itself may be uniform, being itself the product of another natural motive principle.
The contradiction is especially acute when we consider a rotating rigid body in free space, with negligible external torques. When angular velocity is constant, this rotation should continue uniformly and indefinitely per conservation of angular momentum. In analogy with linear momentum, we saw earlier that resistance to angular acceleration is measured by moments of rotational inertia. This suggests that rotation, and possibly other forms of uniform circular motion (for such is the motion of a point on the surface of a rotating body), ought to be considered inertial or natural, rather than forced or violent.
Nonetheless, there is an important distinction, since constancy of angular momentum need not imply constant angular velocity for an isolated system. This is because mass may be redistributed radially, changing the moment of inertia, as when a figure skater draws in her limbs, increasing the speed of her spins. Granted, such redistribution involves an application of force, so a truly inert object will rotate indefinitely at the same angular velocity.
It may seem mathematically contradictory for both linear and angular momentum to be conserved for an isolated system, since angular momentum involves constant change in linear momentum. In physical actuality, however, there is always a symmetry such that the changes in linear momentum for each rotating object in a closed system with no external torques or forces cancel each other out. This is the case for two particles interacting via a central force law. Likewise, a rotating rigid body has zero net linear momentum, as its center of mass is at rest. We may consider each small piece of that rigid body as having changing linear momentum, but each piece is not an isolated system, being forcibly linked to the rest of the rigid body.
The ancients took advantage of the natural regularity of periodic motion to serve as a measure of time. We moderns do the same, using pendulums and atomic vibrations to measure time with far greater precision, while recognizing that celestial motions in fact have measurable irregularities or perturbations. The long-term stability of periodic motion gives us further cause to regard it as something natural or intrinsic rather than violent.
While it is fine to describe perfectly uniform periodic motion in the abstract, Newton did not perceive any physical necessity that uniform motion should in fact exist. We merely define our measures of time in terms of motions assumed to be regular in period, though successive discoveries have shown irregularities in previous measures of time. Even if truly uniform motions do in fact exist, their lack of a priori necessity was, for Newton, a proof that there must be an absolute time, abstracted from any motion, which measures the permanence or duration of things, regardless of whether their motion is fast or slow or null. Time, however, though distinct from motion, cannot be fully abstracted from motion, not only in a relativistic context, but even under classical philosophy, as we have seen. (Sec. 13.2)
In principle, one might define natural and violent movement of quality and quantity, depending on whether such change results from an intrinsic tendency or an external force. Aristotelians restricted these concepts to local motion, however, and Cartesians and Newtonians tended to reduce all physics to local motion anyway. Indeed, since quality and quantity are intrinsic accidents, it would seem that any violent movement in these properties must be mediated by an external force. This force is one of local motion, unless we admit that the quality or quantity of another substance may communicate itself to the first.
Aristotle found it puzzling that there were no recognized counter-natural
alterations or increase or decrease. We have noted that these are all intrinsic movements, while violent movement must have an origin that is extrinsic to the object of violence. (The converse need not hold, i.e., a movement of extrinsic origin need not be violent or counter-natural.)
Still, he speculates that some processes besides local motion, notably generation and destruction, may have counter-natural modes. For example, perhaps dying painfully rather than pleasantly is counter-natural, i.e., opposed to the intrinsic tendencies of the organism. This line of thought bears some similarity to Eastern philosophy, especially Taoism, where the easiest way, i.e., that which is smooth and free from struggle or resistance, is natural or best. Such an account of biological processes, if valid, might provide a basis for a naturalistic ethics.
In De caelo, 2-4, Aristotle discusses simple motion. Each nature (physis) is a principle of motion or rest, and a simple body
is one that consists of a single element, where an element is a type of substance that is simplest, i.e. uncompounded in nature. Accordingly, simple bodies should have a single, uncompounded principle of motion, and their natural motion ought to be the simplest possible. Aristotle holds that such simple motions must be straight lines or circles, since these are the only simple magnitudes.
Evidently, Aristotle’s notions of simple magnitudes
are informed by Euclidean plane geometry, where all two-dimensional figures can be constructed from the straight line or the circle. One-dimensionally, the notion of geometric extension is intelligible only in terms of the straight line or the circular arc, and more elaborate curves such as the ellipse or cycloid are generated by invoking additional constraints for construction.
This mode of analysis, however, identifies motion merely with the locus of points traversed. Simplicity or singularity of motive principle might instead be defined by the velocity or acceleration generated. Even here, we find that all kinematic measures are reducible to compositions of linear and rotational components, at least in a formal mathematical sense. The impossibility of constructing any other kind of continuous motion without composing linear and rotational motion argues that these indeed are the simplest motions.
It need not follow, however, that any simple bodies so defined actually exist. It could be that, in point of fact, even the most fundamental elements are compound natures, separable only in principle but not in reality. Aristotle considered that a composite nature would have the motion of the element that prevails in the composition. This holds only when the simple motions of each element are either colinear or rotational with respect to the same axis. In these two cases, the resultant motion will be in the direction of the prevailing element, though its magnitude will be diminished by the contribution of the other element.
When both simple motions are linear, but not colinear, the resultant motion will be the vector sum of these motions, in the direction of the diagonal of the parallelogram defined by the geometric representation of these vectors (with lengths proportionate to magnitude). If they are both rotational, but with respect to different axes, there are two mathematically possible modes of composition, depending on the axes. In the case where the axes intersect (either within the object or at some external point in space), Euler’s rotation theorem proves that the net motion is rotation around a single axis, distinct from the axes defining the contributing motions. If the axes of contributing rotations do not intersect, then the resultant motion is simultaneous rotation about an axis and translation along the same axis, i.e. a torsional or screw-like motion. Lastly, if one contributing element has linear motion and another has rotational motion, the result will be to have both motions, since these are independent. This covers all scenarios for two elements. The motion of composites of multiple elements can be determined by successive addition of each element’s contribution.
In antiquity, each natural element was considered to be a fundamentally distinct kind of matter with its own characteristic motion. Cartesian and Newtonian mechanics instead treated all matter as effectively the same in kind, and capable of receiving or imparting any kind of motion. The motion of an object is determined by its own inertia plus the net result of any applied forces. Thus motion is determined by relations with respect to other objects. The only motion-determining quality of matter is mass, which defines the amount of momentum for an object at a given inertial velocity, and also that object’s resistance to acceleration or change in velocity.
If, kinematically, there is only one kind of matter, then the only elements
for which we would have to combine motions are the various massive particles that compose visible bodies. Even the simplest of these bodies could potentially receive any complex motion, though intrinsically, a body only has its inertial linear motion. Rotational motion becomes intelligible only when you have particles composed into a rigid body or a single particle acted upon by an external force.
The notion that linear motion is simplest contradicts the judgment of Aristotle, who noted that the circle is a simpler magnitude than a straight line, since the latter has the opposition of motion toward the center and away from the center. This argument that the line has lesser cosmic symmetry depends on the erroneous notion that natural linear motion is defined with respect to the center of the Earth. Still, there is something to be said for the greater symmetry of angular versus radial motion, in celestial mechanics and even in atomic electron orbitals, which exhibit greater angular than radial symmetry. Without pretending to decide which is simpler, we may regard both linear and angular motion as fundamental aspects of motion.
The idea of simplicity in motion is motivated by a desire to economize on physical principles, not introducing motions more complex than what is needed to account for reality. Recalling that a nature
is defined to be a principle of movement, there can be no more principles than there are natures. Thus a body that has fixed nature over some period of time, subjected continuously to the same circumstances (i.e., there are no violent forces), should have a motion that is simple,
i.e., without jerks or discontinuities. This is because the body is continually exemplifying the motion (or rest) characteristic of its nature. As a result, its motion is uniform,
so that the form of each part of its motion is identical to the form of the whole. Only two kinds of continuous motion meet this criterion in Euclidean plane geometry: circular and straight-line motion. Thus all natural motions, at their most fundamental level, should be composed of circular and straight line motions. An elemental body, i.e., something with a simple nature, not composed of disparate natures, should have a simple motion, i.e. linear or circular, when subjected to no violent forces.
This notion of simple motion defines simplicity according to the form of the trajectory, yet modern calculus lets us define a motion vectorially even at an instant. With this qualification, natural motion should not be seen so much as a combination of circles and lines, but as a combination of linear and angular momentum. Conservation of momentum is a fundamental, invariant law of physics.
As mentioned, Galileo considered the uniform acceleration of freefall motion to exhibit a simplicity indicative of natural motion. Following Aristotle’s distinction of uniform rectilinear and circular motion, he identified freefall motion as the former and horizontal inertial motion as the latter. He believed that inertial motion was actually parallel to the surface of the Earth, and therefore circular. Projectile motion was a composition of this horizontal inertial motion and vertical freefall motion.
In fact, parabolic projectile motion is a composition of linear inertial motion along the horizontal and uniform acceleration in the vertical. The vertical motion may have an upward component, as when an object is thrown upward, while the uniform acceleration due to gravity makes this initial upward velocity decrease until it becomes negative or downward.
Motions due to fundamental forces have uniform acceleration insofar as these forces are constant. In fact, the acceleration due to the Earth’s gravity varies according to distance from the center. The same holds for other forces that vary in strength according to the distance from the source. This is an inverse square law for gravitation and electromagnetism, while more complex distance relations apply to the weak and strong nuclear forces.
Mathematically, all motions are ultimately composites of simple (linear or rotational) motion, just as in Fourier analysis, all functions are composed of harmonics. Is this just a mathematical fact, or does it reflect a composition of physical principles? The fact that conservation of angular momentum is an independent principle, not derivable from conservation of linear momentum nor from Newton’s laws, suggests that rotational inertia is indeed a simple motion
or motive principle distinct from that of linear inertia.
Things that have a nature
induce sensible change by how they are constituted. (Part I, Ch. 3) Per se change means that the source of change is intrinsic to its constitution. Something with a simple nature
ought to have only a simple motion, since it has only one motive principle.
We can now better understand the objections of late Aristotelians to heliocentrism, which implied a composite motion for the Earth, both rotating on its axis and orbiting the sun. This contradicted the supposition that the Earth is a simple body. We might retort that the Earth is composed of many elements, yet for the purposes of celestial mechanics, the Earth may be treated as a simple body, even a point-mass. How then, does this simple body have an elliptical orbit and rotation? Composite motion is possible for animals with muscles that flex and contract, yet the Earth has no such relatively moving parts to account for its plurality of motive principles.
The Aristotelians were actually correct to insist that the Earth has only one natural motion, which is in fact its orbit about the Sun. The elliptical form of this orbit seems to imply non-simplicity, but in fact the source of gravitational motion is not solely in the Earth, but in the Earth-Sun system, which orbits about its center of mass. The non-circularity of orbits reflects the fact that gravitational force is relational between two bodies, not inherent in a single body. Following the standard interpretation of general relativity, we may regard gravitation as the natural
motion, while other forces are violent.
The diurnal rotation of the Earth is a violent motion imparted at its creation, continuing indefinitely. Aristotle, because of his erroneous belief that violent motions dissipate, did not appreciate that violent movements could continue for billions of years with little decay, seeming natural.
Additionally, the Earth moves with the solar system around the Galaxy, and with the Galaxy as a whole, but these are movements per accidens.
[1] There are many different approaches to deriving the principles of relativistic mechanics from each other. The approach given is designed to fit with the present context, discussing inertia.
[2] The four-momentum can also be defined with contravariant and covariant vectors, but this is not relevant to the present discussion.
[3] By contrast, the value of electric potential, even in a given reference frame, may vary by an arbitrarily chosen constant (defining ground
or zero).
[4] Consequent only in this presentation. It is actually preferable to think in terms of momentum conservation as more fundamental, since this holds even in relativistic electrodynamics. Newton's Third Law is universal for mechanics, but for electrodynamics it holds only as conservation of momentum, not as a simultaneous action-reaction principle.
[5] As David Bohm remarks, it is not circular to define force in terms of mass (contained in momentum), since mass, in principle, can be determined without weighing, e.g., by counting the number of like particles.
[6] For more detailed discussion, see: R.J. Hankinson. Natural, Unnatural and Preternatural Motions: Contrariety and the Argument for the Elements in De Caelo 1.2-4
in: Alan C. Bowen, Christian Wildberg, eds. New Perspectives’s on Aristotles De Caelo (Leiden: Brill, 2009)
© 2017 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
| Home | Top |