Intensive and Extensive Magnitudes

Until Bergson, the distinction between extensive and intensive magnitudes was largely ignored by philosophers, and even today the treatment of this metaphysical topic is crippled by a relative ignorance of relevant mathematical theory. In this work, I hope to expound a theory of intensive and extensive magnitudes that makes formal mathematical sense and is also consistent with our intuitive definitions of these concepts. Importantly, such a theory should be congruent with our actual psychological experiences of these phenomena. Intuitively, an intensive magnitude is a quantity that can be perceived in an object as greater than, less than, or equal to the magnitude of the same property in another object, yet we cannot assign a ratio to two unequal magnitudes. For example, in the perception of heat, we may sense that one object is hotter than another, but not that one object is twice as hot as the other. Intensive magnitude exists at least as a psychological phenomenon, but we would like to know more about whether these magnitudes are physically real. Seemingly, for nearly all qualitatively measured properties, an intensive metric may be applied, whether we are speaking of hue, pitch, beauty, dexterity, pain, or practically any other property that is not measured by some spatial displacement. This leads one to suspect that extensive, or numerical, quantity, which can have ratios and addition of unequal quantities, is closely identified with our ability to perceive things as existing in the same space, or being superimposed in the same space. This was Bergson’s view, though I shall argue that superimposition is not at the root of extensivity. First, let us explore what the axioms of an intensive metric would look like, based on our intuitive experience, and see which axioms must be added to create a field of extensive magnitudes.

For simplicity, we shall confine our discussion to real-valued magnitudes, since these are the only physically observable quantities. Quantum wavefunctions may have complex coefficients, but measurement of a property invariably obtains a real eigenvalue, as all operators representing observable properties are Hermitian. The first thing we may know about real intensive magnitudes is that an Archimedean ordering system applies, and all possible magnitudes a_i can in principle be ordered a₁ > a₂ > a₃ > a₄…. This structure corresponds with the reality that I may perceive object A is hotter than object B, which is hotter than object C, therefore A is hotter than C. Addition is commutative and associative, additive inverses exist, and we can define a zero such that for all a_i , a_i + 0 = a_i. We can know one object is hotter than another (a₁ > a₂), or that two objects are relatively close in temperature compared to another two objects of much more disparate temperatures. From this we can derive comparisons of higher order, and summarize this knowledge formally.

Axioms of Intensive Magnitudes

1. Archimedean ordering: a₁ > a₂ > a₃ > a₄ …

2. Commutativity of addition: a₁ + a₂ = a₂ + a₁

3. Associativity of addition: (a₁ + a₂) + a₃ = a₁ + (a₂ + a₃)

4. Additive identity: ∃0 s.t. ∀a_i , a_i + 0 = a_i

5. Additive inverse: ∀a₁ , ∃a₂ s.t. a₁ + a₂ = 0; a₂ ≡ -a₁


Intelligible Statements about Intensive Magnitudes

a₁ > a₂

a₁ - a₂ > a₃ - a₄

a₁ - a₂ > a₃ (Take a₄ = 0)

(a₁ - a₂) - (a₃ - a₄) > (a₅ - a₆) - (a₇ - a₈), and so on.

Intensive magnitudes allow us to construct some fairly complicated inequalities, but equations are more restricted. Aside from the equalities stated in the axioms, we may know only a few simple equations. First, we can know that a₁ = a₁ , the reflexive property which practically defines the equality relation, and might be viewed as more primitive than the field axioms stated above. We may also deduce a logical equivalence between certain equations:

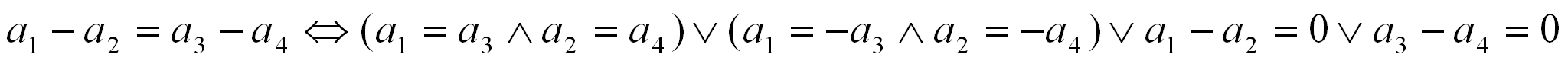
Like the complicated inequalities derived previously, this is not an exceedingly useful class of equations. Returning to our psychological model, this says I can know that the difference in intensity of two pairs of painful experiences is the same if and only if each pair contains an experience equally painful to a member of the other pair, or if the difference is zero. The above expression essentially reduces to the measurement a₁ = a₂; more sophisticated equations are rendered impossible by the absence of multiplication and a multiplicative identity. As long as there is no unit of measurement, I cannot tell whether the disparity between two highly painful experiences is the same as the difference between two mildly painful sensations. Intensive magnitude is a real sort of quantity, but it is crippled by the absence of a useful metric.

Obviously, the deficiencies of intensive magnitudes might be easily remedied by the introduction of a unit of measurement, thereby creating extensive magnitudes. It might be cogently argued that all apparently intensive quantities are purely psychological phenomena, attributable to one’s ignorance of the real metric underlying physical phenomena. In this line of thinking, heat and temperature are really extensive quantities which can be measured in calories or degrees, while pitch and hue are measured by the frequency of sound and light waves. This is certainly true on some level, but it is a mistake to dismiss psychological phenomena as imaginary, and to draw simple equations between the experience of heat and the physicist’s notion of heat. An object at 300 degrees Kelvin is not twice as hot as something freezing at 150 K, since the latter would not be considered hot at all. Heat, as a sensation, is measured relative to some comfortable room temperature. Still, it would not suffice to simply shift our zero point, for we would then have to assume that our level of discomfort with extreme heat is linearly proportional to the number of degrees above room temperature. The problem is even more apparent if we tried to measure how green something is based on its wavelength. We can certainly use light frequency to show that one color is greener than another, with respect to some standard, but this quantification cannot show that one hue is twice as green as another. Intensive magnitude straddles the boundary between quantitative and non-quantitative measurement. Modern physics bases its successes on the intelligibility of quantitative ratios, but is weak in explaining the natural world qualitatively. Why red looks red and blue looks blue rather than the other way around is unanswerable by our purely quantitative theories, which are strongest when dealing with spatial displacement and weakest when trying to account for non-quantitative accidents. The best we can do is show that the existence of qualitative accidents does not contradict the internal logic of quantity; this is the most that so-called emergent properties theories can hope to achieve.

Having reaffirmed the existence and practical necessity of intensive magnitudes, we may next look at extensive quantity in order to decide what is the bare minimum required to distinguish these classes of objects. Extensive magnitudes naturally possess all the axioms of intensive magnitudes, and this field is augmented by the axioms of multiplication. The expression a₁a₂ is unintelligible among intensive magnitudes, either formally or intuitively. We will examine why this is the case more closely, but first note that extensive multiplication is necessarily commutative and associative in our real field, and the existence of a multiplicative identity makes ratio and genuine quantitative measurement possible. The multiplicative axioms afford a mathematical richness to our field that was sorely lacking previously.

Axioms Specific to Extensive Magnitudes

6. Commutativity of multiplication: a₁a₂ = a₂a₁

7. Associativity of multiplication: (a₁a₂)a₃ = a₁(a₂a₃)

8. Distributive property: a₁(a₂ + a₃) = a₁a₂ + a₁a₃

9. Multiplicative identity: ∃1 s.t. ∀a₁ , a₁ ⋅ 1 = a₁

10. Multiplicative inverse: ∀a₁, ∃a₂ s.t. a₁a₂ = 1 ; a₂ ≡ 1 / a₁

Now, for the first time, we can know:

a₁ - a₂ = a₃ - a₄ where a₁ ≠ +a₃ , a₂ ≠ +a₄ , a₁ ≠ +a₄ , a₂ ≠ +a₃

This minimal advancement over intensive magnitudes enables us, by the substitution a₄ = 0, to resolve equations of the form:

a₁ - a₂ = a₃ ⇒ a₁ = a₂ + a₃ where a₁ , a₂ , a₃ ≠ 0

Only when we introduce a metric defined by the multiplicative identity can we perform addition without awkward constraints on the values of the addends. In other words, without the possibility of multiplication, addition is incomplete. Although we can see that extensive magnitude is impossible without multiplication, and that a₁ = a₂ + a₃ can hold much more generally in a field of extensive magnitudes, it may still seem unintuitive that multiplication should have anything to do with the equation a₁ = a₂ + a₃ .

We can address the concerns raised by intuition and elucidate the relationship between multiplication and extension by considering a real example of augmenting a set of intensive magnitudes to create an extensive field. The square roots of prime numbers, their additive inverses, and zero may be regarded as a set of intensive magnitudes. This is clearly an ordered set, with commutative and associative addition, and we can construct intensive inequalities such as √7 - √2 > √5 - √3 . The mutual incommensurability of these numbers results in the same limitations in the construction of equations that we find with intensive magnitudes in general. Most notably, we cannot add two nonzero numbers. Even if we illicitly defined c = √2 + √3, we would not be able to know where c belongs in the ordering of magnitudes (e.g., is it greater than √7?), without further cheating, namely by converting magnitudes to decimals or some other base, which is nothing other than to divide them by a common measure. The necessity of multiplication in order to perfect or complete addition could hardly be made clearer.

In the complete set of real numbers, 1 acts as a measure from which we can construct 1 + 1 = 2 , 1 + (1 + 1) = 1 + 2 = 3, and so on. Since 1 > 0 by choice, it follows that 2 > 1, 3 > 2, etcetera. To construct a similar ordered set of sums in our set of prime square roots, we could take the smallest nonzero magnitude, √2, and construct 2√2, 3√2, and so forth, which might serve as a measure if we were considering all real numbers, but the multiples of √2 are not elements of the field being considered. Without closure under addition, multiplication is impossible. Thus, the key to extensiveness is the ability to add a₁ + a₁ for some nonzero value. Closure under addition follows from the nature of the set of magnitudes rather than the nature of the addition operator per se.

Now that we have achieved some understanding of the mathematical relationship between intensive and extensive magnitudes, we can make sense of the question of whether intensive magnitudes can correspond to real physical magnitudes. Bergson denied the reality of intensive magnitudes, holding that qualities can be treated as quantities, and that any magnitude ought to be measurable. Bergson allows that intensive magnitudes like loudness are orderable, but since they are not measurable they are not true magnitudes. As A.R. Lacey has commented, this is nothing other than to argue that intensive magnitudes are not extensive magnitudes, which no one denies. We have explicitly assumed in our discussion that intensive magnitudes are orderable and not measurable, yet these assumptions are not inconsistent with the possibility that the magnitudes are real and embedded in a field of extensive quantities. Bergson is correct to observe that intensive magnitudes are deficient, as we find that we cannot draw useful equations with them, nor is there any closure under addition. Still, it is arbitrary to deny them the status of magnitude altogether, since our example of the roots of prime numbers shows how intensive magnitudes can become measurable when embedded in a field that preserves the same ordering. Extensive magnitudes impose a measure on intensive magnitudes and attest to the reality of the latter.

There remains the problem of determining whether a physical extensive measure (such as wavelength) truly does measure the intensive property (color) to which we think it corresponds. If an extensive measure is applied to a set of intensive magnitudes and preserves the same ordering, does this suffice to show that it is a true measure of an intensive property? Hardness, for example, is an intensive property. Suppose I propose that hardness can be extensively measured as an inverse of the amount of energy required to break a material. If a series of such measurements is made on any material, and preserves the same ordering we would get by comparing hardnesses qualitatively, does that not provide a strong probabilistic argument that the extensive measure is the objective completion of our intuitive perception? Of course, it would not be an absolute proof. We can distinguish the red end of the visible light spectrum more easily than the blue, even for equal disparity of frequency. So while frequency is the physical basis of color, it does not account for the degree of variation in intensive qualities.

Sets of intensive magnitudes in higher dimensional spaces may be constructed with some difficulty. We might simply cross our set of roots of primes with itself:

If we treat the elements of this set as ordered pairs (a, b) in Cartesian space, it is obvious that the two-dimensional metric does not preserve non-closure, since for example, √(a² + b²) = √5 for a = √2 and b = √3. We can correct this by choosing higher order roots. Even maximizing incommensurability in this way, we cannot avoid some bilateral symmetry of magnitude, since ⟨ a, b ⟩ = ⟨ b, a ⟩. For three dimensions, another two-fold symmetry is added.

Having established the formal means of constructing intensive magnitudes and embedding them in extensive magnitudes, we may now turn to the question of what it means to add and count. With some intensive magnitudes, such as our sets of irrational numbers, we have seen that it is possible to perform limited addition, yet counting with these sets would be impossible. Only with extensive magnitudes, and their more complete form of addition, does counting become possible, counterintuitively suggesting that addition is more fundamental than counting!

Adding, in the most complete (extensive) sense, means combining two distinct non-zero values to arrive at a third value in the same field. The possibility of this operation, we contend, is a necessary condition for the possibility of counting. In this sense alone do we say that addition is more fundamental than counting. Multiplication need not be invoked in order to have counting. On the contrary, multiplication can be derived (for integers) from addition and counting. For example, to compute 2 × 3, we only need to iterate (count) 2 three times, and add all instances: 2 + 2 + 2 (count three two’s, then add them). Thus extensive addition is prior to counting, which is prior to multiplication.

To add two quantities extensively, I must be able to conceive of the sum as existing in the same space (not necessarily ‘physical’ or visualized) as each of the two quantities. By transitivity, it follows that I must be able to conceive of the two quantities coexisting in the same space. This does not imply superimposition.

Added quantities are the same and different: similar enough to be suitable for addition (3 ergs + 5 ergs), yet dissimilar as different parts of a whole, even when equal, as in 4 ergs + 4 ergs = 8 ergs. Addition is fundamentally the operation of combining parts to form a whole, not superposition. If the whole exists in the same ‘quantitative space’ as the parts, this is extensive addition. A space is defined by the kind of quantity that spans it. Generally, intensive magnitudes imply a space with only intensive addition, save for the exceptions caused by symmetry in higher dimensional cases, as discussed above. In geometric or physical space, extensive addition requires that the two lengths/areas/volumes be non-overlapping. Overlapping might be useful for establishing a unit standard, but it is not essential to extensive addition. Extensive addition, in its simplest form, may be depicted:

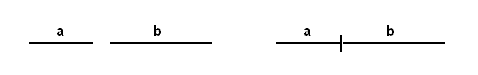
The quantities a and b are abutted or concatenated to form a new quantity that we define to be c₁. This is already more than we can do with intensive magnitudes, though we have not resorted to overlapping. Overlapping is, however, necessary for comparisons. To solve the question, c₂ ≟ a + b, we must effectively conduct this operation:

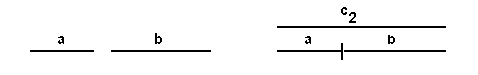
What is the analytical equivalent of this geometric comparison? We need to keep a and b extensively separated, but overlapping with c₂. Analytically, this comparison reads like c₂ – (a + b) ≟ 0. With intensive magnitudes, we are able to say c_i – (a + b) > 0, but here we want to show that c₂ – (a + b) = 0 for some a, b, where a + b represents extensive addition. As an aside, we note that introducing a common unit 1 would just add an extra step:

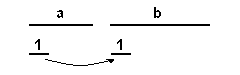
We can now give a treatment of counting that respects both what has been expounded about magnitudes and our psychological intuitions. First, we must distinguish true counting from mere enumerative labeling. The latter would be a simple roll call, where we apply distinctive labels to each object to ascertain which are present. It makes no difference whether these labels are one, two, three, four… or Smith, Jones, Roberts, Johnson…. True counting means answering the question, How many? To achieve this, it is not enough to apply distinct labels to each object, but this must be done in an unvarying sequence, with the name of the last label understood to represent the answer to how many? This process is what every child is taught when learning to count. Pictorial tallies such as those used by Stone Age peoples are evidence of understanding a one-to-one correspondence between the marks and the objects they represent, but they do not necessarily signify true counting, since it is possible that such tallies were mere pictorial representations, without any understanding of two, three, etc. as quantities. If the question, How many? was meaningless to such a person, we would say they have no understanding of counting. Tallying, nonetheless, is a necessary preliminary to counting, since it abstracts the individuality of each object.

When a child learns to count, he is taught the labels one, two, three, etc., with the understanding that each of these is an answer to the question, How many? The child is then taught to apply these labels consecutively to each object in a group, by touching, marking, or pointing at each one without repetition, applying the labels in the order he has learned. The final label used is the answer to how many? This process, substantially more complex than tallying, is what we call counting. A child who has learned to count has effectively learned to add one plus one plus one, etc. If this were not the case, we could not say that he understands any of the labels two, three, four, etc. as signifying quantity. A child who has learned to count knows that if you have one object and are given another object (which is also one), then you have two objects. What is this other than saying that one plus one is two, save for the absence of the plus formalism? Similarly, the child knows that if you have two objects, and add another one, you now have three, and so forth. The child who knows how to count already understands everything that needs to be known about adding one to a natural number. All that he learns when he is taught 3 + 1 = 4 is a symbolic shorthand with new jargon, plus and equals. Learning more sophisticated addition, such as 3 + 2, involves nothing other than counting, albeit a more sophisticated application of counting. The child must learn to consider the objects of two groups as a single group, and count them all together as if they were individuals of the same group. Two dogs plus three cats equal five individual animals altogether. The child is later taught to memorize single-digit sums, so he simply knows them without counting. This mnemonic strategy is what creates the illusion that addition is something beyond counting. In reality, memorizing sums creates the danger of losing consciousness of what numbers signify, reducing them to abstract symbols with arbitrary relationships. The child who struggles to remember how much is 7 + 9 might forget that he can use counting to arrive at the sum, and that the answer to the problem is not a matter of memorizing arbitrary definitions.

As for multiple-digit addition, this is truly a higher order operation than counting, not out of necessity, but out of convenience. Once the child is (hopefully) convinced that the formalism of carrying digits yields the correct result, when compared with analogous counting processes, he can then discard the use of counting and simply rely on the formalism in order to add large quantities, combined with his memorized values of single-digit sums. In this way, we completely remove counting from the process of computing sums, making it seem as though addition itself were conceptually of a higher order than counting, when in fact it is our symbolic shorthand that requires higher cognitive tasks.

Counting alone could not help us to add fractional quantities, for the simple reason that counting contains addition only, and not division, which is essential to the concept of a fraction. Addition by counting would work only for fractions with a common denominator.

© 2007 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org