19. Non-Euclidean and Higher Dimensional Geometry
20. Group Theory
21. Noether’s Theorem
22. Special Relativity: Lorentz, Poincaré, Einstein
23. General Relativity
24. Cosmological Expansion
25. Quantum Mechanics
26. Quantum Field Theory
27. Energy of the Vacuum
Conclusion
In the late nineteenth century, important developments in mathematics would lay the groundwork for physicists’ thinking in the twentieth century. Foremost among these was the acceptance of non-Euclidean geometry as being just as valid as Euclidean geometry. Today, all students of mathematics and physics are taught to accept this equality of standing as an evident truth, though in fact the formal proofs of equiconsistency among various geometries
fall well short of a philosophically rigorous demonstration that non-Euclidean geometry
can describe a real physical space. Such objections were in fact raised during the nineteenth century, when mathematicians and physicists took metaphysical questions seriously, and often had formal philosophical training. By the early twentieth century, however, a new generation of scientists accepted a world where one took for granted the equivalence of abstract algebraic formalisms and non-Euclidean geometric pictures
of physical space. This geometrization of formalisms helped collapse the perceived distinction between physical and mathematical entities. In relativity and quantum mechanics, where physical interpretation of mathematical formalisms can yield metaphysical and even logical absurdity, the result has been a morass of philosophical incoherence. Mathematical models are considered to have explanatory power, merely by virtue of accurately predicting measurements, or saving the appearances.
If we are concerned with physical reality rather than mere quantitative description, however, we shall have to examine modern physico-mathematical developments more critically.
Geometry is so named because it is the science of measuring the world. It originated from the practical arts of measuring real objects like plots of land or buildings to be designed. The Greeks discerned certain principles or rules that were generalizable over any conceivable object that had measure in this world. This capacity for generalization elevated geometry to the level of an abstract mathematical science, as it dealt with fundamental relationships among continuous quantities, abstracted from the determinate manifestations of such quantities. That the sum of the interior angles of a triangle equals that of two right angles is as fundamental a relationship as one plus one equals two,
in the sense that it does not matter whether the triangle is made of paper or wood, just as is it does not matter whether we are adding apples or oranges. We are considering relationships between quantities qua quantities, so geometry is truly mathematical, not merely confined to the physical. Nonetheless, geometry, insofar as it is the measure of the world (geo, earth
), presumes immersion in some space.
Euclid famously theorized that all geometry rested upon five assumptions or postulates. These assumptions reflect directly grasped intuitions about space as we conceive it and as we observe objects in it. They are: (1) a straight line segment can be drawn between any two points; (2) any straight line segment can be extended indefinitely in a straight line; (3) given any straight line segment, a circle can be drawn using that segment as its radius and one of its endpoints as its center; (4) all right angles are equal to each other; (5) if a straight line A crosses two other straight lines B and C, so that the interior angles on the same side of A are less than the sum of two right angles, then lines B and C, if extended indefinitely, will eventually intersect on that same side of A.
These postulates are abstract in that they posit an indefinitely large space, as contrasted with our world, which as far as we know, is of some determinate size. (Even before modern physics, the finiteness of the universe was held as a philosophically demonstrable principle.) They purport to deal with quantity as such, rather than as it is confined in a determinate physical space. We can easily convince ourselves of the truth of Euclid’s postulates by making simple drawings. Yet such demonstration requires immersion in a physical world, examining lines in sand or on a piece of paper, or an imagined medium in our mind’s eye. It is one thing to take for granted that this world is real, but another to assume it is the only possible world. Our intuitive knowledge that Euclid’s postulates are true is not a proof that no other type of geometry would have been possible for a physical universe. Our intuitions do, however, affirm that Euclidean geometry describes the world we actually observe and inhabit.
Before the nineteenth century, it was widely theorized that Euclid’s fifth postulate was indirectly deducible from the other four postulates. Part of the reason for this belief was that the fifth postulate is not nearly as simple an intuition as the other four. Yet such a proof remained elusive, nor could anyone demonstrate that the derivation was impossible in principle.
In 1868, the mathematician Eugenio Beltrami (1835-1900) proved that the non-Euclidean geometry of Lobachevsky and Bolyai (1820s) was as logically consistent as Euclidean geometry, at least for limited regions. That is, if one of these geometries is assumed to be consistent, then the other must be also. In Bolyai-Lobachevskian geometry, there are always two or more intersecting lines passing through a point P that do not intersect some line l not passing through P. In regular geometry, this would be impossible, as it would mean that two intersecting lines are parallel to the same line. This new geometry dispenses with the Euclidean axiom of a unique parallel line through a given point.
In 1871, Felix Klein (1849-1925) showed that all Euclidean and non-Euclidean geometries—including a geometry described by Riemann (1854) where no lines are parallel—were special cases of projective geometry, which considers how figures are altered in shape or size by being projected onto a different surface or viewed from a different perspective. He accordingly called Euclidean geometry parabolic,
Lobachevskian geometry hyperbolic
and Riemannian geometry elliptic,
since each of these conic sections had the same number of points in common with the line at infinity
as the corresponding geometry did with the absolute
(one, two, and zero, respectively). [For the interested reader, I offer a brief discussion of projective geometry and terms such as line at infinity.
] This construction implied that whenever you had a Euclidean geometry you could define a non-Euclidean projection and vice versa. This meant that, as mathematical abstractions, Euclidean and non-Euclidean geometry were equally consistent. This does not imply, however, that non-Euclidean geometry could actually describe a real physical space. Mathematicians, no less than physicists, often conflated mathematical viability with metaphysical viability.
Strictly speaking, it has never been proven that non-Euclidean and Euclidean geometries are equivalent as geometries, that is, as real descriptions of physical space. Rather, the mathematical proofs offered by Beltrami, Klein and others establish only that the algebraic formalisms representing these geometries are equiconsistent. It still requires an intuitive leap to interpret these formalisms geometrically, and in fact no one is capable of really visualizing non-Euclidean space, except by analogy, e.g., on curved surfaces. [N.B.: These are only imperfect analogies; the surface of a sphere is not an elliptical 2-space, since it can have parallel lines (e.g., lines of latitude).] The notion that algebraic formalism is more trustworthy than intuition ignores the fact that the interpretation of formalism depends on intuitions.
Early discussion of non-Euclidean geometries presumed three dimensions, since most mathematicians doubted that higher dimensional geometry was possible, well into the late nineteenth century. This may seem strange to us, since they already possessed enough algebra to construct higher dimensional formalisms. Mathematicians at that time, however, were still philosophically astute enough to recognize that an algebraic formalism alone is not evidence that a real geometry is valid. Today, by contrast, it is taken for granted that any self-consistent formalism purporting to be a geometry has as much validity as any other.
Just as we cannot visualize non-Euclidean three-dimensional space, neither can our mind’s eye conceive of higher dimensional space, Euclidean or otherwise. It is not immediately clear whether this is a limitation of logic, metaphysics, or human psychology.
Why can’t we visualize higher dimensions? After all, we can imagine many things we have never seen. Yet our visual imagination itself constructs a three-dimensional space. Space is the form of our intuition, as Kant said. That is at least true for our visual imagination, and probably for other psychosensory spaces as well. It is because of this limitation in the sensitive faculty, rather than any intellectual shortcoming, that we cannot visualize higher dimensions. Indeed, we can intellectually conceive of higher dimensions, if only in a highly abstract way.
Still, it might well be the case that there are topological, metaphysical, or physical problems that would preclude substantive bodies from having more than three dimensions. Note here we are speaking of real spatial dimensions, not dimensions
in the more generalizable sense of independent variables or properties. Certainly, some of the laws of physics, particularly those electrodynamic equations that rely on a right-hand rule,
require precisely three spatial dimensions in order to be definable. This may simply be an idiosyncracy of our natural order, or it may point to some deeper topological or metaphysical constraint.
Group theory—and its algebraic generalization, representation theory—made possible the discoveries that would unleash the full potential of Lagrangian mechanics. In mathematics, a group is defined by a set with one or more permissible operations that convert elements into other elements of that set. To qualify as a group, the operations on the set must satisfy four axioms: closure, associativity, invertibility, and identity. As an example of closure, the real numbers are a group under addition, so the sum of any two real numbers is also a real number. Associativity means that the order in which we perform the operations does not matter. Invertibility means we can perform the operation in both directions, from element A to B or B to A. Lastly, there must be an identity transformation that maps each element to itself.
Expressed geometrically, groups can represent symmetries. For example, the rotation of a square by 90 degrees in its plane will yield the same square in the same position, so the set of four possible orientations, plus the operation of 90-degree rotation, can be considered a symmetry group. The notion of symmetry is generalizable beyond our familiar Euclidean geometry, and can be applied to various kinds of metric spaces. These alternate geometries
can be defined by different transformation groups that result in the invariance of particular properties. Non-Euclidean geometries are purely formal constructions; their logical consistency does not necessarily imply that a physical space could really have such a structure. Nonetheless, it has been shown that they are as logically and mathematically sound as Euclidean geometry.
Setting aside for now the question of whether alternative geometries
are truly geometries or just computationally useful formalisms, let us examine their importance in constructing theoretical models in modern physics. Klein showed that geometries could be classified according to those properties that remain invariant under a certain group of transformations. In the case of Euclidean geometry, figures are invariant (retaining the same shape and size) under the familiar operations of reflection (mirror image), translation (shifting in position linearly), and rotation. Conversely, invariance under these transformations uniquely specifies Euclidean geometry, so we can formally define geometries in terms of transformation groups.
From the above it is evident that, if we lived in a non-Euclidean world, bodies could change their shape or size simply by virtue of moving linearly or rotating (or being reflected). Hyperbolic geometry is metrically invariant under rotation with involution, but not translation. Non-spherical elliptic geometry is not metrically invariant under rotation. Euclidean geometry is unique in that things do not change shape or size by virtue of moving. Thus, only in a Euclidean cosmos can you have a metaphysical independence of motion, size increase or decrease, and form or shape.
The power of Klein’s Erlanger program,
describing geometries in terms of transformational invariants, was explored more fully by his collaborator, Sophus Lie (1842-1899), who focused on groups under continuous transformations. Invariance under a transformation implies an underlying symmetry, much like invariance under reflection across some line implies our ordinary notion of (discrete) symmetry with respect to that line. When a geometry is invariant under a continuous transformation such as translation or rotation, Klein and Lie realized, there is also a kind of symmetry involved.
Lie developed a theory of continuous symmetry, expressed in the form of continuous groups. Instead of a set of objects with discrete operations, Lie’s groups were continuous manifolds with continuous operations. He developed an algebra to deal with infinitesimal increments of these operations, and then was able to form a proper group theory for groups with these kinds of operations. What came to be known as Lie groups
were defined as any finite-dimensional smooth manifold where the operations of multiplication and inversion (1/x) map smoothly. A particular kind of Lie group, the orthogonal group, would have great importance in twentieth century physics, especially quantum mechanics.
The power of Lie groups would have implications even for classical mechanics, as they made possible Noether’s theorem, which gives an account of physical conservation laws in terms of continuous symmetries. In 1918, the German mathematician Emmy Noether (1882-1935) published her proof that such conservation laws were the mathematical result of symmetries in a system. Each conservation law follows from a symmetry in the calculus of variations as applied to Lagrangian mechanics. Energy conservation, it turns out, can be seen as a mathematical consequence of time invariance; i.e., the supposition that the force laws of physics do not change with time. Other conservation laws also reflect continuous symmetries. Conservation of linear momentum is mathematically equivalent to symmetry under spatial translation, while conservation of angular momentum is equivalent to symmetry under rotation. Noether’s original theorem was applied only to physical systems described by a Lagrangian, though it can be augmented to apply to Hamiltonian mechanics.
Noether’s theorem was not published until after Einstein had unveiled his theory of relativity, and the classical model was already shattered. Still, it had important implications even in a classical context, as it showed that so-called conservation laws,
including the esteemed Law of Conservation of Energy, need not be regarded as fundamental axioms of nature, but could be conceived as artifacts of deeper symmetries. Proof of mathematical equivalence, of course, does not give us the direction of physical or metaphysical causality. It might be that the Law of Conservation of Energy is an artifact of time symmetry, or that time symmetry is an artifact of energy conservation, or that both of these are consequent to some deeper cause. When it is seen that conservation laws are but one possible way of representing physical reality, and not even the most generalized way of doing so, it becomes more tenuous to assert that anything happens or fails to happen because of
the Law of Conservation of Energy or any other such law. Rather, that law is just another way of expressing the observed reality that force laws are time invariant. There is no need, then, to abandon the Newtonian use of force laws as fundamental principles in favor of conservation laws.
At the end of her paper on Invariant Variation Problems
(Invariante Variationsprobleme) which proved the theorem, Noether commented in a footnote that Klein found that the principle of relativity is equivalent to invariance with respect to a group.
In special relativity, this group consists of all Galilean reference frames under a Lorentz transformation. In general relativity, the group consists of all physical reference frames under a more sophisticated transformation, using non-Euclidean geometry. General relativity, in fact, is the only aspect of physics that requires a non-Euclidean geometry of space.
Noether further proved mathematician David Hilbert’s assertion that a law of conservation of energy fails to be necessary under general relativity. This means that there need not be any continuous time symmetry.
Modern relativity theory arose from investigations in electrodynamics. In the nineteenth century, it was widely assumed that light waves propagated through some medium, as do mechanical waves. Accordingly, one might expect there to be variations in the speed of light propagation depending on whether its direction was parallel or perpendicular to the local flow of this luminiferous aether.
Michelson and Morley’s experiment of 1887, however, proved that there is no aether drag,
not even from the Earth’s rotation. Note that the Michelson-Morley experiment did not prove that there is no absolute space, as is sometimes averred. Accordingly, physicists of the time did not immediately leap to the theory of modern relativity.
Nonetheless, the Michelson-Morley null result was a puzzle requiring explanation. In the 1890s, Hendrik Lorentz, operating from the assumption of a stationary aether, developed a transformation that would account for the motion of a system relative to the aether. He introduced auxiliary space and time variables (x', y', z', t') for computing the forces observed in a moving frame of reference. One interesting result of this transformation was that the period of vibration for oscillating electrons would increase by the transformation factor k = √ 1 - (v/c)2 Lorentz considered his auxiliar variables to be mere mathematical contrivances. Physical reality was to be judged with respect to the aether frame. Still, his transformation predicted an observable time dilation effect for systems in motion.
In 1900, Henri Poincaré (1854-1912) took the next big intuitive leap by introducing a principle of relative motion
whereby a state of uniform motion is experimentally indistinguishable from a state of rest. This meant that potentials and their associated forces depended only on the relative, not absolute, positions of objects in the system. Whether or not there exists an aether or absolute space, this has no bearing on the observed equations of motion and forces. In order for the principle to hold—that is, for the same laws of physics to be observed in different reference frames—we must describe phenomena not in a supposed absolute time, but only in a local time
(t') defined by synchronizing clocks using light signals. Since the speed of light is finite, there can be no absolute measured simultaneity of local times.
Poincaré still allowed that there could be a frame of absolute rest in principle, and he computed that the amount of time required for a phenomenon appears to be longer, the faster its reference frame is moving with respect to absolute rest. In practice, we have no way of knowing which is the frame of absolute rest, so we can only compare the local times of known reference frames. Poincaré’s model also replicated, besides this time dilation,
a perceived contraction of length of moving objects predicted by Lorentz.
After correcting Lorentz’s work, Poincaré showed that Lorentz transformations formed a group. Each transformation is a rotation in a four-dimensional space with one imaginary axis, whose metric was defined by the invariant quantity x2 + y2 + z2 - t2. (Poincaré proposed a convention of setting the speed of light equal to 1.) Every transformation (rotation) would result in a dilation. Thus most of the theory of special relativity was already developed before Einstein, without abandoning the notion that there can exist, at least in principle, an absolute reference frame for position and velocity.
In 1905, Albert Einstein (1879-1955) demonstrated that the Lorentzian phenomena of time dilation and length contraction could be derived from two postulates: a principle of relativity similar to that of Poincaré, and the invariance of the perceived speed of light under all inertial transformations of reference frame. This second postulate is wildly counterintuitive: light always appears to be moving at exactly the same speed, no matter how fast we are moving in whichever direction with respect to it. Hand-in-hand with this notion is the abandonment of any notion of absolute rest or a privileged reference frame, even in principle. In Einsteinian relativity, absolute motion is not merely unknowable experimentally, but unintelligible. Space and time are fundamentally relative.
Interestingly, there are no differences in experimental predictions between the Poincaré and Einstein models of special relativity. Poincaré’s model does not require the postulate of the invariant speed of light, so it is more general than Einstein’s. Both Poincaré and Einstein recognize that light alone is not subject to Lorentz contraction, but they have different accounts of light signals from the sender’s perspective. For Einstein, the image of a spherical wave of light always remains spherical in any inertial reference frame, but for Poincaré, it is elliptical if the source is in relative motion to the reference frame, owing to the contraction of the unit of length. In other words, the light wave is lengthened in the direction of the source’s motion. This contradiction of Einstein is only apparent, however, being attributable to differing conventions for defining simultaneity. Einstein defines the travel time of the departing light signal to equal that of the return signal, while Poincaré only requires the round-trip time to be a constant. [Yves Pierseaux, Special Relativity: Einstein’s Spherical Waves versus Poincaré’s Ellipsoidal Waves
(2008) - PDF]
While both the Einstein and Poincaré models of relativity are equally accurate in predicting empirical measurements, the eventual ascension of Einstein’s view would affect the philosophy of physics regarding space, time and events. While Poincaré was agnostic about which model was used, regarding them as mere conventions, Hermann Minkowski (1864-1909) strenuously argued (1908) that the 4-dimensional space defined by the metric x2 + y2 + z2 - (ct)2 described physical reality, and that space and time should be conceived as a single four-dimensional entity: spacetime.
In fact, Minkowski’s model is not the only way to account for the phenomena of special relativity, as Poincaré was already aware of the invariant quantity used for the Minkowski metric, but he chose to define his convention differently. Meanwhile, Minkowski spacetime,
as it follows Einstein’s convention for defining simultaneity, does not allow for spatial dilation, as Hubble commented in the 1920s.
The Einstein-Minkowski model of special relativity also introduced a peculiar notion of event
with important implications for subsequent discussion of causality in physics. An event is represented as a point in Minkowski spacetime, and possible directions of causality are limited by light cones,
that is, cones whose slope are defined by the speed of light. This understanding of causal relationships presumes that there can be no instantaneous action at a distance, but events can cause other events only by the conveyance of an intermediary, which, per Lorentzian mechanics, can never travel faster than light.
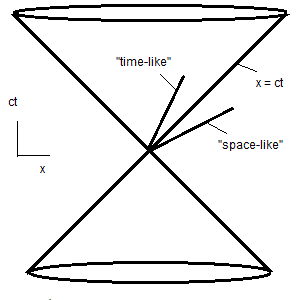Even the weaker claim that there is a one-to-one correspondence between spatiotemporal points and events involves some dubious suppositions. First, we must declare that no more than one event can happen at the same place and the same time. If two bodies simultaneously interact mechanically and electromagnetically, presumably we should have to count this as a single event.
Also, we should have to suppose that nothing happening
in a void (for special relativity allows even an empty universe) would count as an event; indeed, there would be infinitely many events corresponding to each point in empty space at every instant. This practically divorces the term ‘event’ from physically meaningful usage, effectively making it a synonym for ‘spatiotemporal point.’ If ‘event’ really referred to some dynamic interaction, we should have to declare that all interactions are instantaneous (and infinitely local). If we allow any finite time to elapse, the one-to-one correspondence is broken.
The interpretation of spacetime as describing the causal structure of the universe presumes that a cause must always be prior in time to its effect. There is no logical or metaphysical reason, however, why an efficient cause might not be simultaneous with its effect, and of course a final cause could be temporally posterior to that of which it is the final form. When modern physicists make metaphysical claims about causality, it is important to keep in mind that they are often informed by this restricted notion of causality, which at best is a sort of convenient pseudo-geometrical shorthand.
Apart from its philosophically dubious notions of events as spatiotemporal points and events causing events (rather than agents causing events), Minkowski spacetime is conceptually problematic when treated as a real geometry, rather than an algebraic computational device, for several reasons.
First, time is not dimensionally the same as space, so spacetime
does not measure a single thing or kind of thing. The fourth dimension is rendered spatial
by multiplying by c, so it is not really time, but the distance light travels in time t. Yet, since c is constant, the only thing that is really variable is time, so the difficulty is not avoided. Second, a purely spatial geometry already suffices is to give us kinematics. We can parameterize displacements in three-dimensional space with a variable t, and take derivatives to give us velocity and acceleration. Yet if time is also the fourth spatial
dimension, there is a redundancy or contradiction with parameterized treatments of kinematics: we have two t
’s. Third, the negative component to the Minkowski metric entails that areas or volumes can be negative. Such entities may be algebraically meaningful, but hardly constitute a geometry in the sense of measuring some palpable extension. The notion of negative extension is fundamentally incoherent. Again, we are doing algebra, which is geometric only in an analogical sense.
To elaborate the second point, we note that the quantity |dxi/dt|2, where t is a parameter, determines whether a trajectory or world-line
in Minkowski spacetime is characterized as spacelike
or timelike,
according to whether |dxi/dt|2 is greater than or less than zero. A spacelike interval would require a superphotonic signal between the two points or events,
while a timelike interval would require a subphotonic signal, making it possible for the events to be in succession in the same timeline. Yet the t defining velocity in dxi/dt is the parameter t, not the fourth Minkowski dimension (x4).
Regarding the third point, we find that not only area and volume, but even the supposed distance
defined by the norm in Minkowski spacetime can be positive or negative, making this only equivocally geometric. Further, since Minkowski spacetime has a negative component to its metric, the set of all points of distance zero from the origin is not just the origin itself, but the entire light cone. From this we arrive at the curious notion of light being timeless or simultaneous when in transit in free space, though it somehow is able to operate in the temporal world, and be absorbed or emitted. In fact, we are effectively defining simultaneity from light, which is the Einstein convention.
The fourth dimension of Minkowski spacetime is not something that can be thought of as merely superadded to our ordinary conception of kinematics, but rather it transforms all kinematics. This is expressible mathematically as the demonstrable theorem that any manifold within Minkowski 4-space will inherit its metric. Thus even kinematics working within the three Euclidean dimensions (x1, x2, x3) will have the Minkowski metric, with potentially negative distances, areas and volumes in other reference frames. This further calls into question whether the Minkowski metric should be interpreted as a physical geometry, as it seems to insert its bizarre conceptions even where space is assumed to be Euclidean.
While the notion of Minkowski spacetime is conceptually and dimensionally problematic, special relativity provides more cogent, though hardly less radical, insight regarding electromagnetism. Lorentz equivalence shows that electric and magnetic fields are different aspects of a single entity. These fields, considered in abstraction from their sources, are connected in a symmetrical way. Yet, when we take into account their sources, electricity and magnetism are distinct phenomena. So in what sense are they unified? Their effects are indistinguishable; i.e., there is no objective basis for determining which part of an electromagnetic field was caused by static charge or by current. It is the same stuff
caused by different things, or the same thing in a different frame of reference. A charge is static or moving depending on frame of reference, so a field is electric or magnetic depending on frame of reference, but then force is force after all.
We can model electric and magnetic phenomena in any reference frame by using a four-dimensional field tensor (a 4 × 4 array of field strength components). The dimensions
are not of space or time, but degrees of freedom (three spatial dimensions; electric versus magnetic). A four-dimensional potential is invoked, analogous to the vector potential in classical electrodynamics. Under a gauge transformation, we can alter this potential so that we can choose how much of the field strength is charge-induced
(electric) versus current-induced
(magnetic), meaning that this is purely a matter of convention. Though electric versus magnetic depends on reference frame, electromagnetic force is certainly real, and the same might be true of electromagnetic fields. Yet the electromagnetic potential is purely arbitrary and non-physical, much like the classical vector potential. Special relativity, then, should not cause us to abandon the idea that forces and fields mediate causation, while potentials are just constructs.
The Einstein-Minkowski interpretation of special relativity, with its complete disregard for basic metaphysical principles, helped facilitate a certain contempt for philosophy among physicists. Poincaré was one of the last philosopher-scientists who excelled in both domains, while later prominent physicists were philosophical dilettantes at best. The adoption of the wildly counterintuitive, even incoherent, notions of Einsteinian relativity gave rise to a pathological empiricism where even the most serious metaphysical objections were casually dismissed. If a theory seemed bizarre, this only proved that our intuitions were unreliable, and we must defer to the quantitative accuracy of its predictions as proof that it is a description of reality. Thus we find ourselves in an era where mathematical models pose as physical theories, without regard for even the most basic philosophical coherence.
Special relativity, at least, requires us to swallow only one impossibility: that the speed of light is absolutely the same in every inertial frame of reference. This actually understates the case; in Einstein’s interpretation, there is no such thing as an inertial frame of reference
simply and absolutely. Rather, reference frames can only be inertial with respect to one another. Thus, we may say that the speed of light is invariant under inertial transformations. Yet this absurd supposition is unnecessary if we do not adopt Einstein’s peculiar convention for defining simultaneity. The uniformity of the speed of light is not experimentally proven, but a postulate whereby we define our units of length and time. Other conventions are possible and viable. [See: Jong Ping Hsu, Yuanzhong Zhang, Lorentz and Poincaré Invariance: 100 Years of Relativity (2001)]
Later developments in physics, namely general relativity, quantum mechanics, and modern cosmology, have led to even more egregious disregard for philosophical rigor, requiring acceptance of a multitude of logical or metaphysical incoherences (far more serious than mere defiance of common sense
), and resulting in various contradictory notions of causality. We will provide only an overview of such theories, insofar as they bear on the problem of causality.
Although the four-dimensional spacetime
of special relativity has a non-Euclidean metric with an imaginary component (due to the minus sign on the time term), it still presumes Euclidean geometry for the three spatial dimensions. If we hold that the adoption of Minkowski spacetime is purely a matter of convention or formalism, then there is nothing in special relativity that requires us to abandon Euclidean geometry. Non-Euclidean spatial geometry arises only under general relativity as developed by Einstein.
Instead of treating gravitation as another field to be incorporated into special relativity, Einstein considered that the trajectories of free-falling bodies define the geometry of spacetime. These trajectories are geodesics,
or the curves with the locally shortest distance
between two points in spacetime. Recall that, since spacetime uses a pseudo-metric, we speak of distance
only equivocally. Since, under Newtonian gravitation, all bodies fall in the same way (known as the equivalence principle
), one may abstract the trajectories or geodesics from the particular nature of any object, and speak of an intrinsic structure or curvature of spacetime.
The magnitude of local gravitational force is instantly affected by all other mass in the universe, no matter how distant. This apparent action-at-a-distance
was conceptually problematic in classical mechanics, and becomes even more paradoxical when we accept the insight of special relativity that there is no absolute simultaneity at a distance. Such difficulty might be avoided if we considered gravitation in terms of local interaction between massive bodies and deformations in the spacetime metric.
Einstein’s theory was motivated by a need to account for rotating and other non-inertial frames of reference. It could not suffice to have the laws of physics work only in some privileged set of inertial
frames, for reference frames were merely artificial constructs, in Einstein’s view. The law of causality,
as he understood it, required that every cause or effect must be some observable fact, not an artificial choice of reference frame. He was further influenced by the philosopher Ernst Mach, who seemed to suggest that local states were determined as inertial or accelerating with respect to the distribution of matter throughout the universe.
To generalize the principle of relativity over non-inertial reference frames, Einstein postulated that the laws of physics are generally covariant. This means that the laws are invariant under a diffeomorphism, which is a one-to-one mapping between manifolds where the mapping function and its inverse are differentiable (i.e., having no discontinuities or kinks). As a result, the only property of space that appears in the laws of physics is the metric, not any preferred coordinate system (of basis vectors) representing a frame of reference.
In Einstein’s field equations of general relativity, we find that the curvature of spacetime (i.e., its deviation from Euclidean geometry) is a function of the stress-energy tensor, a 4 × 4 array of quantities representing the dynamic distribution of mass, or more strictly, the flux of momentum across each of the four coordinate dimensions. The validity of the field equations does not depend on our choice of coordinate system, so our four dimensions need not correspond to x, y, z, and t, but can be combinations of these.
To arrive at the field equations, Einstein began with Minkowski spacetime and the following axioms. First, assume that spacetime locally resembles Minkowski spacetime, and treat it as a manifold (M). Second, freely falling particles move on timelike geodesics of M. Freely falling means affected by gravity alone. Third is the Strong Equivalence Principle: all laws that hold in Minkowski space continue to hold in manifold M, replacing derivatives with covariant derivatives
(since ordinary derivatives cannot be defined for all tensors). In other words, we do not need to add a curvature tensor to the laws of physics, even though spacetime itself may be described as a Riemannian manifold (roughly, a manifold whose inner product on the tangent space varies smoothly, making possible a well-defined metric and gradient).
Unlike special relativity, which deals with inertial changes in reference frames, we must deal with non-inertial frames to analyze gravity. If we were in an inertial frame with respect to gravitational force, we would feel no force. Rather, when we experience gravitational force, we are accelerating (i.e., in the frame of a falling object) with respect to the body with which we are interacting. Accordingly, Einstein postulated that the path of a free falling body is a geodesic on the manifold M. A geodesic is a curve on M whose first curvature is zero; i.e., the difference in tangent angles converges faster than distance. Simply put, it is locally the shortest curve between two points on the manifold. (In inertial frames, geodesics are locally straight.)
Equivalently, general relativity may be formulated in terms of adding two physical postulates on top of those of special relativity. First, suppose that gravitational mass equals inertial mass. Second, the laws of nature are the same in every frame, not just Galilean frames.
Using the above assumptions, Einstein could show that a gravitational force gradient can be modeled as the curvature of a manifold. In Einstein’s interpretation, gravity is nothing more than the curvature of spacetime, so we do not need any mysterious force. Yet this begs the question as to why spacetime is curved. One may say, as is often done, that mass curves spacetime, but this is just circular reasoning, since we define the curvature of spacetime in terms of the gravitational force. Recall that one of the axioms of general relativity is that the path of a free falling body is a geodesic on the manifold. All that has been proven is that this model is internally self consistent, as it does yield the classical Newtonian force law in nearly flat space.
The spacetime manifold described by general relativity is only pseudo-Riemmanian, since its metric tensor is not positive definite, inheriting the negative ct term from Minkowski spacetime. Thus the geometry
of general relativity is no less specious than that of special relativity, giving us negative distances, areas, and volumes. It is really an algebraic formalism analogically interpreted as a sort of geometry.
Another conceptual problem with general relativity is that it introduces non-Euclidean geometry into space, metaphysically implying that space is a manifold embedded in something else, with respect to which it varies in configuration. The mathematical formalism of manifolds allows us to ignore this metaspace, since we can use local coordinates (i.e., coordinates within the manifold) intead of ambient coordinates (i.e., coordinates with respect to the metaspace), as there is a 1 to 1 correspondence between tangent vectors and vectors in the ambient metaspace. (Using local coordinates, you do not need to specify a path, as in ambient coordinates.) This mathematical evasion is hardly satisfactory, however, as it is empty to speak of something expanding, contracting, or bending, except with respect to something other than itself. Thus the notion of metaspace appears to be at least implicit.
David Hilbert (1862-1943) independently derived the Einstein field equations in 1915. He accomplished this by calculating the Lagrangian of empty space and postulating the invariance of action of spacetime under a general coordinate transformation. This was a [U(1)] gauge invariance, though no one realized this at the time, except for Noether who commented on it. Consequent to this invariance, the field equations are independent of local frame (i.e., choice of coordinates). Further, he found that the action of empty space obeyed a least action principle, which Einstein would express equivalently by saying objects choose the path maximizing time duration.
A field theory of general relativity may also be generated using Hamiltonian mechanics. This involves treating spatial and temporal flux separately. Our choice of direction defined as time
is arbitrary, in keeping with the relativistic view that space and time depend on choice of reference frame (coordinate system). Neither space nor time is an absolute reality, but only the 4-manifold spacetime
is a real physical entity.
It may seem strange to speak of empty spacetime having an action,
as if spacetime were a thing that could move or induce motion, but the essence of general relativity is that the geometry
of spacetime is variable under gravity (or gravity is an expression of this variability), and in that sense can bend,
curve
or warp.
We seemed to have returned to Newton’s conception of space as a substantial thing, rather than a mere accident of objects. Einstein at first resisted this interpretation, considering it absurd to treat space
as an object with physical properties. By the 1920s, however, he became convinced that spacetime was a real physical agent, since the field equations admitted of solutions even in the absence of matter, and the stress-energy tensor could not be defined independently of the metric tensor gμν.
In Einstein’s later view, mass-energy and the metric field were seen as interacting with each other, following the Newtonian principle of action and reaction. Both matter and space were capable of acting and being acted upon. Ascribing such capability to space required an abandonment of Mach’s view that space was a mere relation, and that inertial states were determined solely by the distribution of mass in the universe. Although he came to this position reluctantly, Einstein found it a great advantage that general relativity so interpreted could account for the principle of inertia, placing its cause in the metric field. Otherwise, he found it paradoxical that an inertial system could have causal efficacy on processes without itself being acted upon. He saw this as a Newtonian analogue to that of the privileged center
in the Aristotelian cosmos. This was unacceptable to his epistemological assumption that causes and effects must be observable facts.
Yet Einstein was able to save his empiricist epistemology only by compromising it, permitting that a fundamentally unobservable entity, space itself, should have causal efficacy. There are no privileged positions, to be sure, but space as a whole has the capability once attributed to Aristotle’s privileged center
or to Galilean inertial reference frames.
Einstein tried to soften this implication by selecting a solution to the field equations—the Einstein universe
—where Mach’s principle would hold, and the metric of spacetime was determined solely by mass distribution. Yet Einstein’s static universe was soon recognized as untenable, as it became appreciated that the universe, that is the metric field itself, is rapidly expanding in all directions.
Under Einstein’s interpretation of general relativity, gravity is a distortion of the metric of spacetime. This is a philosophical interpretation, not something that has been proven by experimental confirmations of quantitative predictions. The Einstein field equations predict distortion of the metric by gravitational sources (masses). Experimentally observed deflection of light by the sun has been interpreted as a change in geodesics, since light is presumably massless. Yet this is just one possible interpretation. Alternatively, for example, we may consider this to be an extension of the equivalence principle proved by Galileo, whereby the trajectories of falling bodies in a given gravity field are independent of their mass.
The uncritical adoption of the theoretical constructs of relativity as real physical entities can lead to some gratuitous indulgences in empiricist absurdism. An amateur has said that 1 + 1 = 2 is inapplicable to real world, because v + c = c. This is hardly less rash than the professional physicist’s claim that Euclidean geometry is similarly inapplicable, while the real physical world is described by pseudo-Riemannian geometry. In fact, all we know for certain is that Minkowski spacetime and pseudo-Riemannian geometry are useful abstractions for calculating. There is no solid reason to reify them as physical realities.
Despite his own philosophical daring, Einstein did understand that mathematical correctness does not always imply correct physics. In 1927, the Belgian priest-scholar Georges Lema&icric;tre (1894-1966) solved Einstein’s field equations using astronomical data, indicating that the universe is expanding, and would continue to expand indefinitely, though it began at a single point without a yesterday. Until then, virtually all scientists believed in a static cosmic order. Indeed, the eternity of the universe was a presupposition that underlay the uniformitarianism, necessitarianism, and even atheism of late nineteenth-century scientists. Einstein, sharing this philosophical prejudice of an unchanging, eternal natural order, considered that Lemaître was correct in mathematics, but wrong in physics.
Our concern is not so much with the big bang
theory or the hypothesis that the universe will expand indefinitely, but rather with the implications of the expansion or contraction of spacetime itself. Einstein had already acknowledged that the spacetime manifold may bend or warp, so there is nothing mathematically forbidden about expanding or stretching the manifold out in all directions. Lemaître did not hold simply that galaxies moved away from each other, but rather that space itself expanded, carrying the galaxies away, so that from any point in space, it seemed that all were moving away from the observer, at a faster rate the further distant they were. Edwin Hubble (1889-1953) confirmed this linear relation observationally, after which the expansionary model of the universe became widely accepted.
Even if we tentatively accept that it is possible for space
to expand, as though it were itself a substance, it would seem impossible that we should notice this. After all, if everything in the universe doubled in length along all dimensions, we should not think anything had changed, since all sizes and distances had changed by the same amount, and we could not notice anything. Yet by Hubble’s Law, the more distant galaxies travel faster, since we are seeing them at a time when the universe was younger and expanding faster. Thus, relative to ourselves, we should see them seem farther away than we would otherwise expect, not that we would know what distance to expect. Yet, even then, should we actually expect to see an indication of velocity via observable redshift? After all, the successive waves of light are being emitted within nanoseconds of each other, so we cannot expect the change in expansion rate to be a factor.
Worst of all, from a relativistic perspective, the observed redshift indicates expansion rates much greater than the speed of light! Naively, this would seem to be a refutation of relativity, but on the contrary, we add the absurdity of expanding space upon that of the invariance of light. Anyone thoughtful enough to take the time to try to work this out in an ontologically coherent manner will be frustrated, and correctly suspect that most physicists are not concerned with such coherence. The early Einstein, at least, knew enough philosophy from Ernst Mach that space is not a thing in its own right, but is abstracted from the distance relations between matter. Matter enables space to exist.
Michal Chodorowski has recently suggested [PDF] (2007) that the expansion of space
model is unnecessary to explain the superluminal velocities predicted by general relativity (and violating special relativity). Indeed, expansion of space
taken literally is fundamentally unobservable and should go the way of aether as a physical explanation. Instead of having a chicken-and-egg scenario with matter curving spacetime, and spacetime altering the motion of matter, it is much more parsimonious to say that matter alters the motion of other matter, getting rid of spacetime, which is merely a mathematical construct describing the form in which matter acts on matter gravitationally and kinematically.
M.J. Francis et al. [PDF] (2007), taking note of such criticisms, dismiss Chodorowski, saying all that really matters is making accurate predictions. (All that matters is saving the appearances!) They propose that expansion of space
needs to be reinterpreted, so that it is not some physical force causing effects such as redshift. Rather, it is a framework for understanding general relativistic effects. What expands is not space, but the cosmic substratum, which may be modeled as a fluid. Superluminal recession velocities can be explained with alternative coordinate systems making them unnecessary. In no event is there superluminal velocity from an extended local inertial frame, in any formulation. The Friedman-Robertson-Walker (FRW) metric, whereby expansion occurs, holds only on large intergalactic scales, which accounts for why galaxies and clusters are not pulled appart.
Physicists generally display a better grasp of the notion that space and time derive their existence from matter (or are accidents,
to use the Aristotelian term) when dealing with theories of singularities and the big bang. Lemaître understood that there needed to be multiple quanta before there could be space and time as known under Einsteinian relativity. Of course, this notion of matter prior to time suggests that there is a metaphysical time beyond the time
of physics, again hinting that what Einstein calls time
is something more structured and substantive than the most primitive notion.
If relativity seems to confuse agent with action, substance with accident, it at least tries to hold some self-consistent notion of causality. The same is hardly to be said for quantum mechanics, which seems at times to dispense with any intelligible notion of causality, and even to contradict relativity. [I have treated the ontological problems of the standard Copenhagen interpretation of quantum mechanics in another essay.]
Quantum mechanics uses a Hamiltonian and a conjugate momentum
which is not equal to mechanical momentum. This canonical momentum minus the field momentum gives us the physical momentum. There is no least action principle
in quantum mechanics; that is, given initial and final conditions, there is no unique path that minimizes the action over time. This is because of the form of the quantum Hamiltonian, as contrasted with the classical Lagrangian.
Without going into too much detail, quantum mechanics is relevant to our inquiry for two reasons. First, because of its intrinsic indeterminacy, it seems to wreak havoc on traditional physical notions of causality. This is not a mere change in physical theory, but a challenge to physicists’ perception of their science, which is to explain why and how things happen, that is, to provide a determinate cause. Understandably, many physicists challenged this aspect of quantum mechanics, and tried to open the door for a deeper, underlying determinism. Second, quantum mechanics makes nonsense of the notion that stuff
—be it matter, energy, or aether—is ontologically fundamental. Belief in philosophical materialism was so deeply held among physicists that it remains prevalent to this day in their conceptualizations, notwithstanding its refutation by quantum mechanics.
Indeterminacy in quantum mechanics does not imply acausality, since (1) events can still be determined at least in a probabilistic sense from prior events, and (2) the time-dependent evolution of the wavefunction is strictly deterministic. Still, quantum mechanics requires us to adopt a broader notion of causality, allowing that a single cause might have more than one possible effect. This resembles a return to the Aristotelian view that natural tendencies are not ironclad necessities, after the centuries-long detour into strong determinism following Descartes and Newton. There is also some rough analogy with fluid mechanics and chaos theory, which, though dealing with strongly deterministic phenomena, are effectively probabilistic due to extreme sensitivity to initial conditions. This opens us to a more turbulent notion of causality than that of billiard ball mechanics, where the agent and recipient of an act are clearly distinguished. Quantum mechanics requires us only to go a step further and dispense with the notion of any underlying physical strong determinism.
The time evolution of the wavefunction presents another interesting problem, as quantum phenomena can be modeled just as well using a retarded wavefunction moving forward in time, or an advanced wavefunction moving backward in time. Indeed, quantum interactions may be interpreted as these two wavefunctions meeting and shaking hands.
This would seem to reintroduce an element of final causality back into physics. Recall that a final cause is not necessarily an intelligent purpose, but the final form of an agent’s act. In quantum mechanics, it is at least mathematically meaningful to say that an event is determined by a future form (advanced wavefunction). This was, in a sense, also true of classical mechanics, as Newtonian laws work just as well if time is reversed, but in quantum mechanics we are now dealing with a mathematical construct—the wavefunction—that is believed to be a real physical entity, at least on the level of existential potentiality.
Whatever one thinks of the existential status of the wavefunction, it is clear that palpable, determinate, corporeal states, which we traditionally called particles,
are not the fundament of physical reality. In this sense, materialism is dead. Such states are only consequent to interactions, which we equivocally call observations
(an unfortunate term, suggesting that the presence of a conscious observer is necessary). In between interactions, the particle
is not in any determinate state; it does not even have a determinate mass, energy, position or momentum! All these properties are merely accidents of interaction, not continuously existing determinate realities. Without such determinations, we have no particle
except in a highly equivocal sense. Clearly, the wavefunction, or the physical potentiality that it represents, is a deeper fundament than the observed particle state, and has a truer claim to being the source of physical agency.
Using Aristotelian terms, what physicists have been observing to date are merely accidents, not substances. We measure masses, energies, positions, momenta, which are all properties. There is no palpable corporeal body with a definite size, shape and position underlying these phenomena. When we speak of the radius
of a fundamental particle, we really mean its effective radius in terms of scattering other particles under a specific type of interaction. The value of this effective radius varies according to the type of interaction. There is no longer any notion of a particle as an impenetrable volume of space.
If observed particles are not substances, but merely accidents, whence comes their substantiality? In other words, what is the underlying physical existent upon which these measurable properties depend for their being? It is practically certain that there is such a fundament or substance, not only because of metaphysical considerations, but also because of the evident continuity of existence of each particle, though it may change states from one moment to the next. The quantum wavefunction at least points to the form of that substance, even if we hesitate to say that the wavefunction itself is the substance.
If we acknowledge that the wavefunction is a form of potentiality, then we can arrive (as did Heisenberg) at a neo-Aristotelian account of physical change, from indeterminate potentiality to some determinate actuality. We cannot say, in a given instance, why outcome A rather than B occurred, but we can say that either outcome was within the capacity of the potentiality described by the wavefunction.
A further consideration introduced by quantum mechanics is the possibility of holism in physics, as indicated by entangled states of distant particles. In order to avoid interpreting this phenomenon as action-at-a-distance, it is proposed that by observing one particle, one is observing the whole system, including the distant particle, thereby determining the whole system. This might escape the necessity of one particle transmitting a superphotonic signal to the other, but it still seems to be fundamentally at odds with the relativistic account of spacetime, which renders absolute simultaneity at a distance fundamentally incoherent. Given that we measure one of two entangled positrons, at what time in the local frame of the other positron will the latter appear in the opposite state? Planes of simultaneity depend on the choice of reference frame, so it would seem there can be no definite answer. Either our understanding of spacetime or that of quantum entanglement needs correction or amplification.
With the Pandora’s box of quantum mechanics opened, we once again see the abundant causal possibilities permitted by classical philosophy, though temporarily ignored for much of the modern period. We can no longer afford to be naive about causality. The nature of physical laws is also called into question, as familiar deterministic laws now seem to be statistically emergent artifacts from the underlying indeterminism of quantum mechanics. It no longer makes sense, if it ever did, to say that events happen because of
some law of physics. Yet neither does it seem consonant with the abundant evidence of causality (via the dependence of effects on the presence of agents) to say that our laws simply describe correlations. Rather, they give the quantitative forms specifying how agents may operate in a set of circumstances.
In quantum mechanics, harmonic oscillators can be modeled with annihilation
and creation
operators, which lower or increase the harmonic state by a discrete increment. The lowest oscillation state is not zero, as in classical mechanics, but corresponds to an energy of 1/2 hν, where h is Planck’s constant and ν is the frequency. Due to the smallness of Planck’s constant, this energy is generally quite low, but not zero as we would expect classically. Thus we may speak of the zero-point energy
of a field.
In quantum field theory, particles can be treated as excited harmonic states of some underlying field. Conversely, the excited states of any quantum field can be interpreted as particles, so that all field interactions can be modeled in terms of particle exchanges. Indeed, one of the striking discoveries of quantum field theory is that all field interactions correspond to discrete energies matching those of known particles. Nonetheless, the particle interpretation is not essential to quantum field theory, which deals only with fields as such.
It is with reference to the particle interpretation of quantum field theory that physicists speak of particle creation
or annihilation.
This is not true creation ex nihilo, but an excitation of an existing field, or a return to its ground state.
When theoretical physicists pretend to have solved the mystery of creation, they are conflating two concepts of particle.
On the one hand, due to a lingering nineteenth-century materialism, they still think of particles as the basic stuff
of existence. Yet on the other hand, the particles
of quantum field theory are not fundamental substances, but concretized states of some underlying substratum, which is the field. The field remains as a suppositum, so we do not have genuine creatio ex nihilo.
Roughly speaking, quantum fields may be modeled as ensembles of infinitely many oscillators. The number of degrees of freedom (independent dimensions of physical variation) in such a system is determined by the number of particles in each type of state, but not the total number of individual particles. Thus particles in the same quantum state are statistically identical; there is no way to distinguish this particle
from that particle.
This statistical identity has been interpreted to mean that particles of a type are really identical, not distinct objects, which of course is absurd. Even if particles are statistically indistinguishable, this does not imply numerical identity. Distinctions in position, or even the fact that two particles in a state behave differently from one, suffices to establish non-identity.
In fact, quantum field theory underdetermines metaphysical interpretations, not only for the question of individuation, but also as to which fields
(if any) are real or which particles
(if any) are real. It only shows the computational equivalence of field and particle models. This has led modern physicists to adopt an expanded materialism, which regards particles and fields as the sum of all existents.
We can now re-examine the notion of spacetime as a substratum, in light of general relativity, cosmological expansion and quantum field theory.
From observations of cosmological expansion, the energy density of the vacuum is measured to be small but likely non-zero. How can this be?
According to general relativity, a positive energy density (i.e., the presence of mass) as such such slows down cosmic expansion, but the presence of a positive energy density in the vacuum itself creates negative pressure, increasing expansion. In light of the fact that cosmic expansion seems to have accelerated even long after the big bang, general relativity suggests that the small energy density of the vacuum is positive.
By vacuum
we mean space in the absence of mass, not an absolute void. The fact that the vacuum is energetic suggests again that there is more physical reality than particles, making conventional materialism untenable. Instead, we might consider the vacuum of spacetime
as a sort of field, which might be regarded as a substance, rather than the metaphysical or relational notion of space.
Quantum field theory does not provide a satisfactory solution for the energy of the vacuum. Taking the sum of the zero-point energies of the vibrational modes of quantum fields, we would have a fantastically large vacuum energy density, assuming space is at least as fine-grained as the Planck length. If space-time is a continuum, then we could have arbitrarily short wavelengths, making the zero-point energy infinite. This impossible result is one reason that quantum theorists postulate that space must be grainy,
even though this creates other absurdities. Yet under neither circumstance do we arrive at the low zero-point energy consistent with general relativity and measured by cosmologists.
Since quantum field theory ignores gravity, it cannot determine the absolute energy density of the vacuum, but only relative density. By adding an arbitrary constant, one might reconcile the QFT prediction with cosmologically measured values.
The energy of the vacuum, in some theories, is invoked to account for the origin of mass in particles. This mass is not created out of nothing, but from energy stored in the vacuum. We cannot detect this energy just by looking at the vacuum; it is hidden from view, and enters our experience only through interactions, such as those supposedly mediated by the Higgs boson. This notion of an energetic field behind
the observable void suggests again that spacetime
is not really space in the metaphysical sense (the geometric medium of extension). Perhaps instead we should call it a field that alters kinematic relationships. This would eliminate the need for the illogical convention of regarding empty space itself as energetic. To attribute energy to a void violates that most basic metaphysical axiom, accepted even by Epicurus, that from nothing comes from nothing. Yet we see that the "energetic vacuum" is anything but a void.
We have consistently seen that mathematics underdetermines metaphysics. Although mathematical models can provide a detailed quantitative description of physical reality, they do not thereby explain reality, for they do not give us the non-quantitative aspects of reality, which includes causality. The logical order of theses in a mathematical theory need not reflect the metaphysical or physical priority of the objects it represents. If physics is to be a theoretical science, and not just a practical, computational science like engineering, it must be grounded in sound metaphysical interpretations, without which it cannot have any real explanatory power.
The history of mathematical physics shows the dangers of assuming that our models depict fundamental reality. Practically every generation thought it was on the verge of understanding fundamental reality, only to have a new level of physics overturn previous certainties. How can we know that current models are fundamental? One can never prove there is no more physics, nor can any physical theory remove
Mathematics may help us to visualize aspects of nature that are not directly detectable by the senses, and to make our descriptions of nature more accurate quantitatively. It is far from obvious, however, that such descriptions have real explanatory power, and we have seen that some constructs, such as relativistic spacetime, might be misleading when interpreted as real physical agents. Diverse mathematical models may accurately describe the same set of observations, and a single model may admit of diverse physical interpretations.
Counterintuitive relativistic effects such as time dilation, Lorentz contraction, and gravitational lensing have persuaded most physicists to believe in mathematical models as descriptions of physical reality, no matter how many basic physical, metaphysical or logical intuitions are laid waste. In their view, the paradoxes of relativity and quantum mechanics do not prove the incoherence of the standard interpretations of these theories, but only their supposed profundity. Thus physics has achieved an intellectual decadence comparable to the extravagant speculations of ancient Greek philosophers and late Scholastic theologians.
Due to the anti-metaphysical prejudices of modern scientists (especially Anglophones), mathematics has taken on the role of metaphysics, a role for which it is ill-suited. Theoretical physicists effectively equate the mathematically possible with the metaphysically possible, which is why they see nothing restraining them from taking pseudo-Riemmannian geometry and the paradoxical Copenhagen interpretations of quantum mechanics as literal physical reality. If you can write equations for something without internal contradictions, then that model is something to be taken seriously as a possible explanation of physical reality.
In fact, mathematics is not even a metaphysics of quantity, much less a general metaphysics. Mathematics is an a priori science, while metaphysics deals with a posteriori principles. Mathematics deals with what is logically possible when dealing with pure quantity, which in some respects is much broader than what is coherent when dealing with supposed physical entities and their causal relations. Just because something does not involve a contradiction considered as a mathematical abstraction, this does not mean that there is no contradiction if you consider it as a concrete physical object.
Modern physicists try to think in geometric terms whenever possible. This is intuitively helpful, but sometimes it can mislead us into thinking that mathematical objects are
Newtonian mechanics was governed by algebraic
What, then, of the symmetries themselves? Are these just brute facts, or is there a reason for them? For example, time symmetry cannot be accounted for by Newton’s laws of motion, for that would be to use Newton’s laws to prove that the laws themselves do not change with time. An additional principle would need to be invoked to account for the presence of such a symmetry. We are still left with the problem of how a mathematical relation can be the efficient cause of any physical event. We need to suppose real agents that, for whatever reason,
Some German philosophers, notably Max Stirner and Friedrich Nietzsche, rejected the notion of nature following laws, seeing this as informed by bourgeois sensibility about rule of law. Instead, objects do whatever they can, exerting their power as much as possible, and what we call
The rules or laws do not themselves cause physical events, but rather they are descriptions of the natural order whereby the powers of physical agents are defined. Efficient causation is to be found in the actions of physical agents, using their defined powers.
The billiard ball style interactions of Newtonian mechanics are the very paradigm of causality for most students of physics and other natural sciences. Although modern physicists pretend that mathematical analysis can yield insights into causality for quantum mechanical and relativistic systems, it is telling that mathematics fails to give an account of causal priority even for classical mechanics, since it is time-reversible. If mathematics cannot help us resolve the notion of physical causation, perhaps we should examine our intuitions about billiard ball interactions, to at least define the metaphysical problem of efficient causation.
When body A collides with body B, we ordinarily say that the motion of body B is caused by the collision. Body A imparts some of its momentum onto body B, causing it to move. This way of speaking combines two notions of causality, often conflated in physics. One is the notion of events causing events. For example, we said that the motion was caused by the collision. This is really just a temporal sequence; what we really mean is that the action of some body caused action in another body. If we were to speak simply of events causing events, we could never arrive at any notion of causality beyond temporal correlation. This is exactly what Hume, Russell and others proposed when they suggested rejecting the notion of causality. The problem with causality, however, is not intrinsic incoherence or vagueness, but its irreducibility to mere temporal correlation. Real physical causality, as Newton intuited, involves a real transfer or imparting of action from one agent to another. This is why the mechanists, who had a strictly corporeal view of physical substance, believed that objects could only act upon each other through direct spatial contact. Body A moves body B when the two collide, but it is really A acting upon B.
This analysis makes sense if we believe in absolute motion, but the problem becomes more complicated under the modern idea that all motion is relative. In that case, there need not be any real distinction between the mover and the moved, as that would depend on choice of reference frame.
Relativity also makes it difficult to say what constitutes an action. Energy and mass, which respectively might be considered the capacity to exert force and the capacity for inertia, depend on reference frame. Whether something is active or inert seems to depend on our perspective, rather than reflect an objective reality. Electric charge and various quantum mechanical quantities, at least, are conserved even relativistically. Under general relativity, however, inertial frames are not privileged over accelerating frames, leaving undefined which object is the actor and which is acted upon. This is why Einstein identified his theory, in later years, with a strenuous assertion of Newton’s principle of action and reaction. The two are indispensable and inseparable.
Yet the principle of action and reaction, whether applied to billiard balls or to mass interacting with the vacuum of spacetime, may create a chicken-and-egg scenario that is metaphysically and logically problematic. If there is any metaphysical principle that physicists accept in some form, it is that we cannot get something for nothing. If it were otherwise, there would be no reason to search for the cause, origin or reason for anything. Causality needs to have an order of priority, or else nothing is really explained. If neither cause nor effect is metaphysically prior, both cause and effect are merely unexplained brute facts.
Notwithstanding these problems, Newton’s suggestion that force is the medium of causation seems most promising, and consistent with developments in modern physics. As it seems that everything, even particles themselves, can be modeled as force fields, we might look to force as physically real causation.
Even relative quantities such as energy and momentum should not be dismissed as manifestations of real agency. Just because their quantitative values are not absolute, this does not mean that they are not real physical phenomena. It may be that various dynamical variables are different aspects of some real physical agency.
In physics, time plays an important role in defining the direction of efficient causality, as this can go from past to future, but never from future to past. Mathematical formalism, however, often works equally well in either direction. (Statistical mechanics breaks this time symmetry.) An understanding of time as distinct from space is practically necessary in order to understand causality. Yet if space and time are really merged in a 4-manifold, with the
Perhaps we should look for causality not in the links from one phenomenon to another, but in the principles governing the behavior of physical systems. This could be a least action principle, in one of the several varieties discussed, or a sort of integration over possible paths, if the Feynman diagrams of quantum interactions are interpreted literally.
We must be careful to distinguish genuine logical or metaphysical incoherence from mere contradiction of our common sense intuitions. Not every apparent paradox or absurdity discussed might turn out to be genuinely incoherent. Since mathematics underdetermines metaphysics, we will need a properly metaphysical inquiry into causality, in order to judge which interpretations of physics are genuinely or only apparently problematic. While many would balk at making physics somehow subject to the judgment of metaphysicians, we have seen that, on their own, physicists effectively practice metaphysics, and generally do a poor job of it. Yet if they were to abandon metaphysical interpretation altogether, physics would be reduced to mere description without causal explanation. The relationship between physics and metaphysics need not be adversarial, but on the contrary should be complementary. Our survey of physical theory has given us a wealth of material that we may subject to rigorous metaphysical analysis (reserved for future work), which in turn may enrich our physical understanding above mere computation.
Projective geometry arises from perspective drawing, where we try to represent three-dimensional objects on a plane. To accomplish this, we must depict parallel lines as converging at a point on the horizon. The rules for such construction are expressed in theorems derived in a Euclidean context, so projective geometry is Euclidean in its theoretical foundations. That is to say, it presupposes Euclidean geometry, though a projective space is not itself Euclidean.
In early formulations, from the seventeenth century to the early nineteenth century, projective geometry was described by mathematicians as a Cartesian plane augmented by a
The real power of projective geometry was made apparent in the 1827, when Möbius used it to develop homogeneous coordinate systems. Every line through the origin in three-dimensional space may be taken as corresponding to the point at which it intersects a projective space, such as the z = 1 plane. For the lines that do not intersect the projective space; i.e., the lines in the x-y plane, we may represent each set of parallels as corresponding to a point on the line at infinity. In projective geometry, all that matters are the ratios of the three-dimensional coordinates, since the lines through the origin deviate from the point of intersection with the projective plane by a constant coordinate ratio. We can represent the coordinates in projective space as [x/z, y/z], like a Cartesian plane.
The utility of the above construction is evident when we reverse the direction of transformation, starting with a Cartesian plane (dimensions x1 and x2) and treating it as though it were a projective space for some three-dimensional space. Each point on the plane corresponds to a line through the origin in 3-space, with the equation ay1 + by2 + cy3 = 0. This equation with zero makes the coordinates homogeneous. In physics, homogeneous coordinates are useful, for example, in determining center-of-mass coordinates, and many other applications.
© 2013 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
probable error
Saving the appearances
is no proof of explanatory power.
out there
in some real space. We must remember that we could just as well dispense with geometric models and treat things analytically or algebraically, though this would be more difficult for us to conceptualize.
laws
of force relations, from which we could calculate equations of motion. Modern geometrical analysis has helped bring to light that these laws may be thought of as consequent to symmetries. Indeed, some choose to speak of the symmetries themselves as physical laws, or at least as fundamental features of nature. If the symmetries themselves do not exactly cause physical events, they seem at least to have real physical implications. Indeed, in modern particle physics, breaking a symmetry is said to cause a reaction.
obey
physical laws.
laws
reflects the limits of their power, either intrinsically or when encountering some other power. Still, it is inarguable that physical objects have finite abilities, and so the question of why their limits are here rather than there is answerable only by some kind of rule or law.
temporal
dimension a matter of perspective, it would seem at first glance that we cannot have well-defined causal direction. Still, relativity does manage to preserve a principle of causality.
Appendix: Projective Geometry
line at infinity,
effectively serving the function of a horizon, where parallel lines converge. Each set of parallel lines with a given orientation "converged" to a different point on the line at infinity, which might be visualized as encircling the Cartesian plane at some infinite distance. Obviously, this representation was purely analogical, since parallel lines do not converge, and infinity
is not some definite quantity or distance. Still, projective geometry could be computationally useful insofar as it enabled objects in three-dimensional space to be represented with just two variables.
Home
Top