Part I: Logical Functions of Linguistic Elements
Part II: Propositions
8. Sentences and Statements
9. Affirmations and Negations
10. Truth, Falsity, and the Principle of Contradiction
11. Simple Predicate Propositions
12. Universal and Particular Quantifiers
13. Contradictory and Contrary Opposition
14. The Excluded Middle
15. Propositions with Negative Terms
16. Composite Subjects and Predicates
Part III: Non-Indicative Moods
We have now defined all the necessary components of a sentence representing an affirmation. We need a noun (in nominative case) to represent a subject, and a rhema that gives the predication of being, with an existential mode that is built into an action verb, adjective or adverb, or is represented by a separate term. These two components, subject and predicate, we recall from grammar school, constitute a sentence. A sentence is a linguistic object, either spoken or written. The meaning that it signifies is called a statement.
Since a sentence consists of at least two components with independent meaning, it is a logically synthetic tool. It takes two or more concepts and prompts us to consider their ontological or logical relationship. The sentence, therefore, is the first linguistic tool that requires us to definitively move beyond our intuition of individual concepts and synthesize them according to some logic.
Formal logic has traditionally been concerned with a particular kind of statement called a proposition. This is a statement that proposes (“puts forward”) its content (subject and predicate in relation to each other) as true or false on some level. The mood of a sentence determines if it represents a proposition or some other kind of statement. Mood, we have seen, can be represented in a verb’s conjugation, but it can also be conveyed by the overall construction or tone of the sentence as a whole. ‘You are walking’ might represent a proposition, unless we change the order of the words to ‘Are you walking?’ or change our tone to ‘You are walking?’ The interrogative mood does not propose the truth or falsity of its content, but solicits such a proposition from the hearer. The imperative, optative and cohortative moods express a desire for what is said to become true: ‘Walk toward me!’ or ‘(I hope) you will walk toward me,’ or ‘Please walk toward me.’
Since logic is concerned with truth and falsity, Aristotle regarded sentences of non-indicative moods to be irrelevant to logic, being matters of rhetoric or poetry. This dismissal is perhaps unjustified, since even sentences of other moods must have a subject and predicate, and therefore have some internal logical structure. We will consider the statements represented by these other kinds of sentences much later, after we have completed an extended discussion of propositions.
We note that statements in general, and propositions in particular, are not linguistic objects, but the meanings of sentences. For Aristotle, a proposition (apophantikos, “that which shows forth something”) is simply a type of sentence that affirms or denies something. He says every sentence (logos) has meaning (semantikos), but not every sentence is a proposition. Modern philosophy more clearly distinguishes the linguistic from the semantic, so that what we call logic deals principally with the latter and only incidentally with the former. We recognize that, properly speaking, a sentence cannot affirm or deny anything, but it represents an affirmation or negation. All propositions are affirmations, negations, or compounds of these.
When a subject and predicate are coupled in the indicative mood, they express a statement that proposes a fact or state of affairs, namely the ontological relationship between predicate and subject. When I say, ‘The sky is blue,’ I propose as a fact (in whatever level of reality being considered) an ontological relationship between “blue” and “the sky” (in this case, where blue is a property of the sky). A fact may be proposed positively or negatively; that is, we may assert the fact either in affirmation or denial. If, being uncertain of a fact, I neither affirm nor deny it, I cannot be said to propose anything. One may propose a fact as more or less probable, but these are just modal qualifications of affirmation and negation, as we shall see later. For the present discussion, we will consider only two kinds of simple propositions (with a single subject and predicate): affirmations and negations.
Most languages express negation by introducing an adverb such as ‘not’. This syntax can be ambiguous, for the sentence, ‘The sky is not blue,’ appears to express the negative of “blue,” but in fact the statement is negating the relationship between “sky” and “blue.” It is really negating the “is,” whether “is” is expressed as a copula or not. Negation alters the mood of the sentence, since it changes the relationship between subject and predicate that is to be understood by the sentence. Some languages, reflecting this insight, have a distinct grammatical negative mood. Indeed, we may say that the indicative mood can be subdivided into the affirmative and negative moods.
The affirmative and negative moods are related to one another by the principle of contradiction. Two simple statements with the same subject and predicate contradict each other when one statement is expressed in the affirmative and the other is in the negative. By ‘contradict’, we mean that they assert opposite things. As noted in our previous discussion of opposites (Introduction to Ontological Categories, VI), an affirmation and negation are related so that, to the extent that one statement is true, the other is false. Thus the notions of truth and falsehood are very closely bound to the notions of affirmation and negation. We may see this by examining the notion of negation more closely.
The Greek terms for affirmation and negation are kataphasis and apophasis, where phasis means “assertion” or “information.” A kataphasis is “near” or “against” what is asserted, while an apophasis is removed or “away from” what is asserted. Thus the affirmative and negative moods signify the speaker's position with respect to what he speaks. He may distance himself from what he speaks or declare himself in agreement with what he speaks. That which is asserted or proposed is the semantic content, or meaning, of the logos apophantikos, the sentence representing a proposition. We understand propositions as semantic objects, not linguistic objects, so we might refer to a proposition simply as apophantikos, since Greek allows the use of adjectives as nouns.
Negation in Greek is expressed by two terms: ou and mé. Ou is used much like the English ‘not’, except in prohibitive clauses where it is replaced by mé. Mé is used with imperative, subjunctive, and infinitive clauses. It carries the sense of forbidding something or introducing what is to be avoided. The Latin equivalents of ou and mé are non and ne, respectively, though their usage is somewhat different. Ne is used in subjunctive and imperatives to indicate the prohibition or at least the undesirability of an action, but it is not used with infinitives. There is a consistency in this difference, since in Greek an infinitive may be used adverbially to express the purpose or result of the action it modifies. This can also be done in English, e.g., ‘I have come to help you.’ Such usage could also be found in early Latin, but by the classical era, there was no longer a purposive infinitive, except in poetry and in the phrase ‘dare bibere’ (“to give to drink”). As a consequence, there would no longer be a need to use ne in infinitive clauses, since ne, like mé, expresses a negative purpose (avoiding, preventing or forbidding).
The purposive sense of ne is contained in the Latin negare, which means “to refuse” or “not to allow.” To deny or negate something is to say “no” to it. Indeed, ne is the original Latin term for the negative response, “No,” though later Latin used non as the negative response, and passed this to the Romance languages. Ordinarily, we say “no” in response to a request: “Shall this be done?” “No.” Someone proposes an action, and the denier refuses to allow that it should come into being, regarding the action as forbidden or undesirable. Similarly, when a proposition is denied, the denier refuses to allow that what the proposition signifies should be.
The Greek verb meaning “to deny” is arneomai, which is possibly derived from an-rheo, the absence of utterance. Rheo is the verb form of rhema. Arneomai, then, is to “unsay” something, or to declare the absence of what the utterance, the rhema, signifies. We have seen that it is essential to a proposition that some existential relationship be posited, and this may be represented by the copula ‘to be’ or incorporated into some other term.
The basic notion of negation entails a declaration of the absence of the existential relation proposed. Suppose we consider the expression ‘sky blue’ as a sentence proposing an existential relationship such that blue is in the sky as the accident of a subject. We may propose this relationship positively or negatively, declaring where we stand with respect to the content. One may say “The sky is blue” or “The sky is not blue.” ‘The sky is not blue’ means nothing more than a declaration that we hold the existential relationship represented by ‘is’ in ‘The sky is blue’ to be absent. Granted, we may hold other positions besides simple affirmation and negation, for we can consider a relationship to be possible, probable or necessary, but all of these stances admit of a negative opposite. We could contrarily declare that something is not possible, not probable, or not necessary. Thus affirmation and negation are the most fundamental modes of declaring a proposition.
It would seem that negation is a psychological phenomenon, since it entails that we will to give or refuse our assent. However, willing need only be considered in the abstract, so the notion of negation is not bound to the particular psychology of any individual or species. Similarly, the fact that concepts are only intelligible to a mind does not mean that they are purely psychological phenomena, since they can be considered in abstraction from any particular mind that contemplates them.
A negative statement negates (declares the absence of) the existential relation represented by the copula, not necessarily any particular term in the statement. For example, the negation of “The sky is green” denies or declares the absence of the existential relationship signified by ‘is’. There may exist such a thing as the sky, and there may exist such a thing as green, but we deny that they are related in the manner signified by ‘is’, in this case representing a subject-accident ontological relationship. We typically represent the negation of this statement by the sentence ‘The sky is not green,’ but this syntax is ambiguous, as ‘not’ may seem to modify ‘green’ rather than ‘is’. The negative statement “The sky is not green” should not be confused with the statement “The sky is non-green.” “Non-green,” if it is to be a concept with real content, is a species consisting of all accidents that are contrary to green or incapable of coexisting with it in the same subject. If “non-green” were simply the absence of green, then the statement “The sky is non-green” would be problematic, as it would declare an absence, a mere nothing, as if it were ontologically predicable of a subject. Further, we would have to say non-green is the same as non-red, since nothing is nothing. This is absurd, of course. By “non-green,” we really mean a broad species of accident analogous to the set-theoretic complement, not a nullity.
The ‘non’ in ‘non-green’ does not mean the same as ‘not’ in ‘is not’, for the latter declares the absence of a relation, while the former declares the presence of some indeterminate entity other than green. The two kinds of negatives have a similarity of course, since the predicate “non-green” does logically imply the absence of green, yet “non-green” is more than a mere absence of green, while the ‘not’ in ‘is not’ signifies nothing but the absence of the relation signified by ’is’.
The statement, “The sky is not green,” understood as the negation of, “The sky is green,” declares the absence of the existential relation between subject and predicate signified by ‘is’. The predicate is not directly negated; this is not the same statement as “The sky is non-green.” “Non-green” is not a negation, but a predicate defined as the complement of green. “Non-green” has real conceptual content insofar as there are colors or accidents other than green. If ‘non-green’ were considered to signify only an absence, it would not represent an entity. Nothing is nothing, so there would be no distinction in meaning between ‘non-green’ and ‘non-blue’. In actual usage, of course, these terms do represent distinct concepts, so they must mean more than a mere absence. We can more easily appreciate the conceptual reality of negative predicates in cases such as “impermeable” or “indestructible,” which can be formulated positively as “airtight” and “everlasting.”
Although we regard negative predicates, i.e., complements, as having real conceptual content, the same is not as obvious in the case of true negations, i.e., negative propositions or statements. The Greek sophists famously claimed that sentences of the form ‘X is not Y’ have no conceptual content, since we cannot speak of that which is not. To this we may respond that the sentence, ‘Socrates is not tall,’ does have content. Although it does not articulate a state of affairs, it allows us to make judgments about states of affairs given certain conditions. For example, if we stipulate that Socrates exists and has the dimension of height, we know from the sentence ‘Socrates is not tall,’ that Socrates must be short or of medium build. Negation does not say anything by itself, but in combination with other statements it does convey conceptual content.
The distinction between the two kinds of negative statement (one is a true negation; the other is a complement predicate) can be represented in symbolic logic if we retain a copula. ‘~(x is P)’ and ‘x is ~P’ are semantically distinct sentences, and the negative symbol ‘~’ actually represents different things in the two sentences. In the first, it expresses negation of the proposition “x is P.” In the second, it does not negate any proposition, but signifies the logical complement of the predicate P, or “non-P.” The scope of this complement depends on the scope of allowable predicates of x. The distinction between negation and complement is lost when we drop the copula from our symbology. The sentence ‘~P(x)’ is syntactically ambiguous, and could correspond to either of the semantically distinct sentences ‘~(x is P)’ and ‘x is ~P’.
For complex sentences, consisting of propositions coupled by logical connectors (AND, OR, etc.), it is important to distinguish which propositions are being negated. If we use a particle such as ‘~’, we can enclose the negated propositions in parentheses. In this way, we can distinguish ‘~(p AND q)’ from ‘~p AND ~q’. Another approach is to use a bar over that part of the sentence that represents what is negated. With this notation, we would write these same two sentences as ‘p AND q’ and ‘p AND q’ respectively. The first system of notation is analogous to the use of the adverb ‘not’ in ordinary language, while the second system resembles the negative mood. We can express both the negative mood and the complement predicate without a copula if we combine these notations, so that ‘x is not non-P’ would be rendered ‘~P(x)’, using the particle ‘~’ to signify the predicate complement, and the overline to signify negative mood.
In discussions of symbolic logic, it is common to characterize negation as an operator that reverses the truth value of a proposition. This is a purely syntactic definition of negation, motivated by the grammar of Western languages, which use the adverb ‘not’ to negate the expression it modifies, rather than have a negative grammatical mood. The effect of negation on a proposition’s truth value is not the essence of what it means to deny something, though it is a necessary consequence of negation, as we shall see presently.
Consider a simple proposition, “x is P,” denoted by ‘P(x)’, understood in the affirmative sense. As an affirmation, “x is P” is a logical judgment that a certain relationship between x and P is present in some reality. If that judgment is correct, meaning the affirmed ontological relationship is indeed present in the reality being considered, we say that the affirmation is “true.” If, however, the judgment is incorrect, meaning the affirmed ontological relationship is absent from the reality considered, we say the affirmation is “false.”
We note that:
Suppose we consider the same proposition judged negatively. The negation “x is not P,” denoted by ‘P(x)’, is a judgment that the ontological relationship proposed by “x is P” is absent. If this judgment is correct, and the ontological relationship is indeed absent from the reality being considered, we say that the negation is true.
With both affirmations and negations, truth and falsity depend on the judgment being correct or incorrect, where correctness is determined by a correspondence between the judgment’s assessment of the existential status (present or absent) of an ontological relationship in a given reality and the actual state of affairs. For a judgment to be true, such a correspondence must exist. If an ontological relationship is affirmed as present, it must really be present; if its presence is denied, it must really be absent. For a judgment to be false, there must be no such correspondence. If an ontological relationship is affirmed as present, it must be absent; if it is denied, it must be present. As long as the ontological relationship is well-defined, it is at least hypothetically possible to determine its presence or absence. Presence and absence admit of no intermediate when they are predicated of the same thing in the same way at the same time.
Now, let us simultaneously consider the affirmation and negation of the same proposition. (1) If the affirmation is true, the negation must be false. (2) If the negation is true, then the affirmation must be false. This is nothing other than the principle of contradiction. We can prove both these statements (1 and 2) easily. If the affirmation is true, the proposed ontological relationship must be present in reality. This presence would falsify the negation. If the negation is true, the relationship is absent so the affirmation is false.
The converse of these statements also seem to hold. If the negation is false, the relationship must be present, so the affirmation is true. If the affirmation is false, the relationship must be absent, so the negation is true. These statements can hold only if we insist that a relationship must be either present or absent, so we are necessarily dealing with logically coherent propositions. For this reason, “false” is not simply “not true” without qualification. Nonsense expressions or single words may be considered “not true,” but neither are they false. Well-defined propositions, by contrast, are necessarily true or false with respect to a reality, even if we do not necessarily know which is the case. The principle of contradiction and these converse statements also depend on the necessity that the relationship is proposed in the exact same way in both judgments, save that one is an affirmation and the other a negation. Only then are we justified in maintaining the mutual exclusivity of the presence and absence of this relationship in a given reality.
The astute reader will have noticed that I have not really given a logical proof of the principle of contradiction, but rather a conceptual account of it in terms of truth and falsity, which are defined by correspondence to the presence or absence of ontological relationships. The principle of contradiction is built into our raw intuition of presence and absence as being mutually exclusive. Once we give our assent to this, it is not too difficult to show the mutual exclusivity of truth correspondences for affirmations and negations.
We have said that a logical judgment is true when there is a correspondence between the judgment and reality. This is merely a formal definition of “true,” not a practical epistemological rule for determining when something is true. The correspondence is not an ontological entity in the reality being considered, but refers simply to an agreement between the state of affairs conceived by the proposition (the presence or absence of some ontological relationship) and the state of affairs in reality. This agreement does not entail identity, for a conceptualized state of affairs is not the same as a real state of affairs. The relationship between the conceptual subject and predicate of the judgment, “The sky is blue,” is not identical with the real relationship between the actual sky and the color blue. However, the logical relationship between “sky” and “blue” does represent the ontological relationship between the actual entities these concepts may describe. We say the logical judgment is true when the ontological relationship represented by the judgment has the existential status (present or absent) indicated by the judgment.
Note that a negation can be “true” even though it does not articulate a definite reality. “True” and “real” are not the same, since truth is not predicated of ontological entities, but of judgments, based on the correspondence between judgments and reality described above.
The principle of contradiction may be applied to innumerable different hypothetical realities, and it will hold in each reality. As a result, we find that the negation of a proposition is true in any reality where the affirmation is false, and the affirmation is true in any reality where the negation is false. The converse holds for both these statements in each reality. If we could consider the set of all possible realities, we would find that the set of realities where the affirmation is true (and the negation is false) is the complement of the set where the affirmation is false (and the negation is true), and vice versa. Only in this indirect sense could we say that truth and falsehood are complementary.
This notion of a judgment being true or false in different realities should not be confused with the idea of “consistent” theories in formal logic. ‘Consistent’ simply means that there is no logical contradiction among the axioms of a theory or anything that can be deduced from them. It is possible for both the affirmation and negation of a proposition to be consistent with the same theory, but not with each other, since they cannot both be true in the same reality. For example, consider a theory with a single axiom (A): “The sky is blue.” This theory is consistent with either the affirmative proposition (B1) “The moon is yellow,” or its negation (B2) “The moon is not yellow.” In other words, {A, B1} and {A, B2} are consistent theories, but {A, B1, B2} is not.
Above we have spoken of the objective truth and falsity of judgments as determined with respect to some hypothetical reality. Yet a judgment also contains its own subjective truth value that is proposed in the act of its utterance. When I affirm “x is F,” I simultaneously declare that I consider the affirmation to be true. It would be incoherent to say that I affirm “x is F” yet hold the affirmation to be false. Since the affirmation is itself a judgment, it carries its own subjective proposed truth value (which we may compare with reality as discussed above). We may recognize that “The moon is made of cheese” is a false statement with respect to physical reality, but the person who affirms, “The moon is made of cheese,” necessarily judges the affirmation to be true. A negation is essentially a judgment that the corresponding affirmation is false, since “I deny that x is F” means only that I refuse to allow the reality of “x is F” (as the affirmation would assert), and I need not posit any determinate positive idea about what is true. Thus, we may write the affirmation and negation of some proposition P as follows:
Affirmation: ‘I find that Paffirmed is true.’
Negation: ‘I find that Paffirmed is false.’
The syntax in the above formulas is circular, effectively saying “I judge that this judgment (Paffirmed) is true.” Both ‘I judge’ and the affirmative mood in ‘Paffirmed’ refer to the same act of judgment. This redundant syntax is used to distinguish the logical content ‘Paffirmed’ from the subjective truth valuation that is inherent in declaring a judgment.
In other words, all logical judgments carry an intrinsic subjectivity. As we have said previously, affirmations and negations may be judged objectively by comparison with some reality. Yet suppose we make such a comparison and find that Paffirmed is false. That finding is itself a judgment with a subjective dimension, namely the negation: “I find that Paffirmed is false.”
In both formulas, “I” is some arbitrary, hypothetical intellect with volition. It may be objected that this construction mixes psychology with logic. In fact, it is purely logical to acknowledge that logical judgment requires an intellect and will. Beyond that, no characteristics of the psyche, human or otherwise, need to be specified. Some prefer to pretend that intellect and will are not necessary for an affirmation or negation, and would reduce logic to an abstract symbology. This would make logic completely arbitrary, as you can define syntax any way you please. In practice, of course, logicians always make the assumption of an intellect and will when they interpret logical symbols as statements, but they do this only implicitly, whereas I have chosen to make this explicit.
Our observation that truth and falsity are predicated of judgments is ample remedy for the misguided contrarianism that would admit exceptions to the principle of contradiction. These supposed exceptions are generally of two varieties: linguistic paradoxes and set-theoretic paradoxes. Self-contradictory sentences do not represent coherent judgments. For example, the Liar’s Paradox, ‘This sentence is not true,’ does not represent a coherent logical judgment, for the intellect intending such an utterance would subjectively regard it as true. Linguistic paradoxes are purely syntactic, and such sentences have meaning only in their parts, not as a coherent judgment. The paradoxes of set theory are even further removed from logic, since they depend on weaknesses in Russell’s formalism that could be cured by applying the logic of ordinary language to self-reference substitutions. (Trotter 1995)
We recall from our treatise on ontological categories that it is conceivable for entities to be universals or particulars. Universals have essences that may be “said of” some subjects, while particulars may not be “said of” some other subject. A particular entity may simply be the instantiation of some universal essence, or it may additionally possess some incidental attributes that do not pertain to that essence. It is not necessary, for the purposes of this discussion, to decide whether or not universals (or particulars, for that matter) are metaphysically real. We are only going to consider the logic of applying the distinction between universal and particular to propositions and their terms.
When terms are related in simple propositions of the form ‘X is Y’, the significance of ‘is’ depends on whether the terms represent universals or particulars, substances or accidents. We summarize all the possible combinations in the table below. For brevity, we apply modern terms to classical concepts: ‘object’ here means a particular substance; ‘kind’ means a universal substance; ‘trope’ means a particular accident; ‘property’ means a universal accident. For convenience, we will say that these entities are subjects and predicates of propositions, though strictly speaking, it is the concepts of these entities that compose the proposition, and the words representing these concepts that constitute the grammatical subject and predicate. However, as discussed in the Introduction to Ontological Categories, we may also speak of entities being ontologically predicated of one another, as it is this ontological relationship that our sentences represent.
| X | Y | Example | Significance of ‘is’ |
|---|---|---|---|
| object | object | John is Mr. Smith. | (1) identity |
| kind | object | N/A | N/A |
| trope | object | N/A | N/A |
| property | object | N/A | N/A |
| object | kind | Socrates is a man. | (2) X instantiates Y |
| kind | kind | Man is an animal. | (3) X is a subgenus/species of Y |
| trope | kind | N/A | N/A |
| property | kind | N/A | N/A |
| object | trope | not used | (4) X is the substratum of Y |
| kind | trope | N/A | N/A |
| trope | trope | This brightness is this brightness. | (5) identity |
| property | trope | N/A | N/A |
| object | property | The moon is white. | (6) X exemplifies Y |
| kind | property | Fire is hot. | (7) X is differentiated by Y |
| trope | property | not used | (8) X instantiates Y |
| property | property | Green is a color. | (9) X is an accidental subgenus of Y |
Of the sixteen permutations, only nine are logically viable propositions. When both subject and predicate are particular objects (1), the term ‘is’ signifies simple identity. This type of identity could be a simple renaming (‘John is Johnny’), or it could have some logical content, e.g., ‘Louis is the king of France,’ or ‘This cat is my cat.’ Whenever the predicate is an object, the subject cannot be a kind, trope, or property, since an object cannot be “said of” anything, as discussed in Part I of the Introduction to Ontological Categories.
When the predicate is a kind and the subject is an object, (2) ‘is’ signifies instantiation. When both the predicate and the subject are kinds, (3) the subject is a subgenus or species within the genus signified by the predicate, unless subject and predicate are related by identity. Both the instantiation relationship and the subgenus relationship are types of the “said of” relationship discussed in the treatise on ontological categories.
When the predicate is a kind, the subject cannot be an accident, since the essence of a universal substance cannot in any way pertain to an accident. An accident cannot instantiate a universal substance, but only a universal accident. Much less can it exemplify or be identical with a kind, nor can it be a subgenus of a universal substance.
When the predicate is a trope and the subject is an object, (4) we could say ‘This leaf is this green’ to signify that the trope inheres in the object, or inversely that “this leaf” is the substratum of “this green.” In actual practice, ordinary languages do not use tropes as predicates, since the determinate individuation of the trope is already specified by the object, so an exemplification proposition with an object and property suffices to convey all ontological information.
A trope cannot be predicated of a kind, since it is nonsensical for a universal substance to be characterized by an individual accident. A kind can be instantiated by an object, which in turn may have accidents. If these accidents are not essential to the kind, they do not pertain to the kind in any sense. The object may exemplify the differentia that are essential to a kind, yet the instantiations of these accidents are not in the essence of the kind. “An albino is white,” means the property “white” is essential to the kind “albino,” but “this white” or “that white” are by no means essential to the universal “albino,” which is utterly indifferent to the existence or non-existence of particular tropes. It is incoherent for a universal to possess non-essential accidents, so there is no way a trope can be predicated of a kind.
A trope can be predicated of a trope, (5) only in the sense of a simple identity. Unlike an object, which may have accidents that are non-essential to its universal, a trope is nothing more than the instantiation of its universal. This limits the range of logical content when we predicate tropes of tropes. The predicative relationship can be a simple renaming identity, or a description of the trope more or less generically, as in ‘This green is this coloration.’
A trope is not predicable of a property, since an individuation cannot be “said of” its universal. The only distinction between a trope and the property it instantiates is universality, which does not admit of predication from an instance. If the trope is not an instance of the property, then they can have no essential relationship whatsoever.
Properties have the richest possibilities of predication, as they can admit entities in any of the four ontological classes as subjects. Properties are in this sense predicates par excellence. In a similar fashion, we might regard objects as subjects par excellence, since they can take predicates from any of the four classes. For this reason, we may view the object-property relationship, called exemplification, (6) as the quintessential type of ontological predication. When we say an object exemplifies a property, we mean that the essence of the property is somehow to be found in the object. This can be conceived as a determinate instantiation of the property inhering in the object, or as the object instantiating a kind differentiated by the property. Property-object ontologists would characterize exemplification as a primitive relationship, without recourse to kinds or tropes, but this position is problematic, as we showed in a previous work.
When a property is predicated of a kind, (7) we say that the kind is differentiated by the property. The property or differentia is part of the essence of a kind, making a specification within a genus. We might also attribute a property to a kind if it is a differentia of a higher genus of that kind.
When a property is predicated of a trope, (8) the trope instantiates the property. In actual ordinary language, this type of proposition is not used. We do not say, for example, ‘This green is green,’ since we do not ordinarily distinguish properties from tropes. We can signify that an accident is determinate by identifying the determinate object in which it must ultimately inhere. Since ordinary language does not make use of tropes, relations (4) and (8) are replaced by exemplification, which is equivalent to their composition.
Lastly, properties may be predicated of properties (9) either by simple identity or as a more or less generic property.
In sum, there are nine conceivable types of simple affirmative propositions; four identities or generalizations within a class, and five ontological relationships between classes, shown in the diagram below.
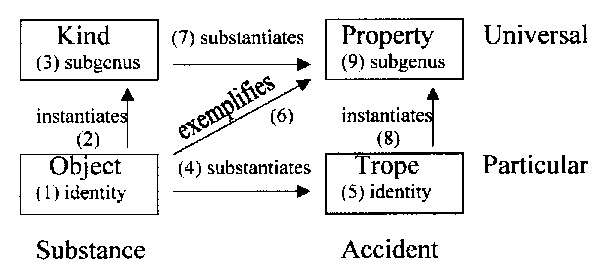
We see from the diagram that all the subject-to-predicate relationships tend from objects to properties. The non-identical intra-class relationships are consistent with this trend, going from the specific to the generic. This reinforces our earlier claim that objects and properties are quintessential subjects and predicates respectively. We will therefore concern ourselves primarily with the relationship of exemplification, as this implicitly contains composites of the other inter-class relationships.
In classical logic and most modern formalisms, simple propositions modify their subjects with the quantifiers ‘every’, ‘some’ and ‘none’. Most logic does not bother with tropes, since the determination of a property is specified by the object, so only properties and kinds might serve as predicates. Each of these predicates can be used in four types of quantified simple propositions, usually classified as follows.
| Proposition Type | Predicate Type | |
|---|---|---|
| Kind | Property | |
| Universal Affirmative | Every man is a critic. | Every man is wise. |
| Universal Negative | No man is a critic. | No man is wise. |
| Particular Affirmative | This man is a critic. | This man is wise. |
| Particular Negative | This man is not a critic. | This man is not wise. |
The supposedly universal quantifier ‘every’ is perhaps too weak to make the subject a universal. When we say, ‘Every man is a critic,’ we are not necessarily saying anything about the universal “man,” but only about individual men. It could simply be the case that every man who happens to exist is a critic, but this does not tell us anything about what it means to be “man.” We could expand the scope of ‘every’ to include all conceivable instantiations of the universal, but this would not make the subject a universal. The full meaning of the so-called universal affirmatives would really be:
Every individual who is a man is a critic.
Every individual who is a man is wise.
More precisely:
Every individual who instantiates the species “man” instantiates the species “critic.”
Every individual who instantiates the species “man” exemplifies the property “wise.”
If we really wanted to make the subject a universal, we could simply say, `Man is a critic,’ or `Man is wise.’ We consider these two utterances to represent false statements, since “man” conceptually is not a subgenus of “critic,” nor is “wise” a differentia of “man” or of any higher genus. However, we may recognize these as true statements: “Man is an animal;” “Man is rational;” if we accept that “man” is a subgenus of “animal” and “rational” is a differentia of “man.”
Notwithstanding the meaningful distinction between statements about universals and statements about all their conceivable instantiations, we might discern a logical equivalence between these two types of statements. If one universal substance (kind) is a subgenus of another, it necessarily follows that every conceivable instantiation of the subgenus must also instantiate the higher genus. (For the purposes of this argument, a kind may be regarded as its own subgenus.) Similarly, if a kind is differentiated by some property, if follows that every instance of that kind must exemplify the property.
The converse of these statements also hold. If every logically conceivable instantiation of a kind also instantiates another genus, it follows that the first kind is a subgenus of the second. An object instantiates a kind insofar as it has the essence of that kind. Since all logically conceivable instances of the first kind also instantiate the second kind, this means it is logically impossible to have the essence of the first kind without having the essence of the second kind, which means the essence of the second kind is contained in the first.
Similarly, if every conceivable instance of a kind exemplifies the same property, it follows that this property is a differentia of the kind, or of a higher genus. Again, an object instantiates a kind by virtue of having its essence, so we are saying that it is logically impossible to have the essence of a certain kind without exemplifying a certain property. Exemplification of a property is equivalent to instantiating a kind characterized (i.e., differentiated) by that property, so if every instance of species X exemplifies property P, then every instance of X is also an instance of some kind Y characterized by P. As stated previously, if every conceivable instance of a kind is necessarily an instance of another kind, then the first kind is a subgenus of the second. Thus X is necessarily a subgenus of Y (again, a kind may be its own subgenus), where Y is characterized by P. As we showed in our discussion of ontological categories, a subgenus necessarily has all the differentia of its higher genera, so P is also a differentia of X.
We may summarize these logical equivalences formally.
X is a subgenus of Y ⇔ Every instance of X is an instance of Y
X is characterized by P ⇔ Every instance of X exemplifies P
In both cases, logical equivalence holds only if we consider ‘every’ to mean every conceivable (i.e., logically coherent) instantiation, and not merely every actual instantiation. This logical equivalence does not mean that a species is simply the set of all conceivable instantiations, but that statements about the species tell us something about every member of the set, and vice versa.
In modern set theoretic formalization of logic, usually little effort is made to distinguish a universal from the set of its instantiations, or between conceivable instantiations and actual instantiations. Instead, the so-called universal quantifier ‘for every’ (∀) is assumed to be the only meaningful concept of universality, and the range of ‘for every’ is defined by some set. The distinction between conceivable and actual is unnecessary in mathematics, since all of its “objects” are (conceivable) abstractions. It is a mistake to extend this lack of distinction onto a logic of real objects, where it makes a real logical difference whether we mean every conceivable object of a kind or every actual object of a kind. It is also the case that a universal is not exhaustively specified by its dependence relations with instantiations.
We have shown previously that mathematical “objects” are really universals. (Introduction to Ontological Categories, Part II) Thus sets of mathematical “objects” will be sets of universals. Set theory effectively treats universals or abstract ideas as though they were objects. This can be a convenient shorthand, but it can also lead to paradox, as I shall show in another work.
What exactly is the universal quantifier doing? It cannot be simply counting across instantiations, since there could be uncountably many possibilities. If there are infinitely many (countable or uncountable), subtracting one element leaves the same cardinality, yet logically there is a big difference between ‘every’ and ‘not every’. In actual practice, we often say ‘every’ without clearly conceiving what the set of “every X” would look like. What we really mean by ‘every X’ in that case is to define a class of individuals that instantiate the universal X. All we really have in mind is the universal, from which we can make general statements about the individuals that instantiate it, even if we have no idea what the set of conceivable individuals looks like. So, although ‘every’ taken literally is a set theoretic term, in actual usage it often intends statements about universals rather than a clearly conceived set.
It is true that when we clearly conceive of a universal, we have at least formally defined the set of all conceivable instantiations, but it does not follow that this set is clearly conceived. For example, I may have a clear concept of what “blue” is, so that I can make universal statements involving it, such as, “All blue objects look cool.” This is a perfectly clearly conceived statement, for I know that the color blue, eo ipso, makes an object look cool, so it is unnecessary for me to think of every possible type of object that could be blue, if I were even capable of such a thing. Similarly, if I know that the very notion of being a quadruped entails having feet, I do not need to check if each individual quadruped has feet, much less contemplate the range of all conceivable objects that might be considered quadrupedal. In fact, the logical power of universals lies precisely in the fact that I do not have to conceive of ridiculously immense sets of hypothetical objects. If I understand the essence of the universal, it is not necessary for me to contemplate all its possible instantiations in order for me to make generalizations about those instantiations.
To negate a universal affirmation, we may say, ‘Not every man is a critic,’ or ‘Not every man is wise.’ These are logically equivalent to the statements signified by ‘Man is not a critic,’ and ‘Man is not wise,’ where we consider “man” as a subgenus of “critic,” and “wise” as a differentia of “man.” Clearly, if even one individual is an exception to the rule, there can be no essential relationship between the universals in these statements. We signify this situation by applying ‘not’ as a complement operator, to the effect that some number of men other than every conceivable man is a critic, or wise. This is different from the standard form of negation, ‘Man is not a critic,’ where ‘not’ represents the negation of the relationship between subject and predicate.
‘Not every’ is not a quantifier in the sense of giving a number of elements, since an infinite set minus one element still has the same cardinality, yet there is a profound logical difference between ‘every’ and ‘not every’. We can represent this distinction it set theoretic terms. When we say ‘every element of X’, we mean all the elements of X, considered one by one, not as a single collective: {x1, x2, x3… xn} To capture the concept of ‘every’ in this formalism, we must not regard the bracketed “set” as anything more than its elements, notwithstanding the common practice of treating sets as though they were elements of other sets. When we say ‘not every element of X’, we are making an indeterminate designation, which could apply to any proper subset of X, including the null set.
Formally, we might say that the ‘not’ in ‘not every’ is effectively a complement operator, so that ‘not every X’ is the complement of X in the power set of X. The power set of X is the set of all possible subsets of X, treating each subset as an element. This common mathematical practice is equivocal, however, since a set is not an element of another set in the same way that its own elements constitute it. A more precise representation of ‘not every’ would be:
{ø} XOR {x1} XOR {x2} XOR {x1, x2} XOR {x1, x2, x3} …
This is similar in form to the complement of X in its “power set,” but instead we apply the properly logical “exclusive OR” (‘A XOR B’ meaning “A or B, but not A AND B”), rather than the set theoretic version of the inclusive OR, which gives a union of sets. When we use the exclusive “or” here, we mean that ‘not every’ signifies an undetermined member of this list of possible subsets, but not more than one of them simultaneously. When I say, ‘Not every man is blond,’ this means it is conceivable that (1) only John is not blond, or (2) only Jack is not blond, or (3) only Jack and John are not blond, but not that any two of these possibilities can be simultaneously contemplated as a coherent reality.
We can show that:
‘Not every X’ is Y ⇔ ~ (Every X is Y)
The forward implication holds regardless of which of the many proper subsets of X we choose to represent ‘not every X’. All of these proper subsets exclude at least one element of X, so it is not the case that every X is Y. Note that this implication holds only if we interpret ‘not every X’ as positively excluding the possibility of ‘every X’ being the subject. When we choose a proper subset to represent ‘not every X’ in the statement, we interpret that subset as excluding the other elements. For example, we could say ‘Not every continent is an island,’ where ‘not every continent’ refers to Australia. However, ‘Australia is an island,’ does not exclude the possibility that all continents are islands, unless we understand this assertion as positively excluding other continents from this predication. When we say ‘not every’, we do in fact make such an exclusion, just as when we say ‘not all of them’.
The reverse implication also holds, for if it is not the case that every X is Y, then the only remaining possibilities are that some or none of the elements of X are Y. These possibilities correspond precisely to the subsets of X signified by ‘not every X’.
There is a logical equivalent to the negation of the universal affirmative that is conceptually much simpler, without resorting to a consideration of all possible subsets. It is:
There is some instance of X that is not Y.
By considering those instances or elements of X that are not Y, we do not need to think about power sets and the like, but only need one instance of X to establish the proposition. This proposition is an indefinite version of the particular negative. Perhaps unintuitively, the indefinite particular negative is the negation of the universal affirmative.
The universal negative is not the negation of the universal affirmative. Rather, it is a contrary affirmation using a contrary quantifier ‘no’. By ‘contrary’ I mean an opposite extreme, beyond what is necessary for mere negation or contradiction. Rather than assert that “every X is Y,” it would suffice for the purpose of negation or contradiction that “not every X is Y.” The universal negative goes further than this, and insists that “no instance of X is Y.” It may equivalently say that “every X is not Y,” a statement more obviously deserving of the name ‘universal negative.’ Formally, this parses as:
Every instance of X is ~Y.
For every xi in X, ~(xi is Y)
In the first sentence, we consider the negative particle as a complement function on the predicate Y, so ~Y signifies some indeterminate predicate that is exclusive of Y. In the second sentence, we represent “X is not Y” using the negative mood discussed previously. This version of the universal negative asks us to consider each of the members of X as being the subject of Y. As stated previously, in ordinary language we often do not have a clear concept of what all the members of a universal are, but we make statements based on our understanding of the universal itself. The essential relationship among universals signified by the universal negative is as follows.
(Y is a kind) X is not a subgenus of Y.
Example: No rock is an animal.
(Y is a property) Y is not a differentia of X.
Example: No plant is rational.
When we make truly universal negative statements, we declare that “rock” is not a subgenus of “animal,” and “rational” is not a differentia of “plant.” Yet more than this is logically implied, for neither could an animal be a subgenus of rock, nor could any rational object be a plant (that is, a plant cannot be rational even incidentally). In universal negative statements, subject and predicate are mutually exclusive; their essences are somehow inherently contradictory.
The subject of a universal negative statement seems conceptually problematic. Consider the universal negative: ‘No rock is an animal.’ What is signified by the subject ‘no rock’? If it is a mere nullity, how can anything be predicated of it? Clearly we do not mean there is some nullity “no rock” of which “animal” is predicated. The expression is a shorthand meaning that there is not any rock of which it is true that the rock is an animal. In other words, of all conceivable individual rocks, not one is an animal. (Again for this to be truly universal, we must considering all conceivable individuals.) Alternatively, we may say that for every conceivable individual rock, that rock is not an animal. This is logically equivalent to “rock” and “animal” being contradictory universals; i.e., it is impossible for a rock to be an animal, as it is contrary to the essence of “rock.” This is because the essence of “rock” lacks one or more of the differentiae of “animal.” We do not need to consider every single rock in existence or conception to know this; we only need to grasp the universal. Again, if we were only dealing with actual individuals, the fact that no rock is actually an animal would not by itself prove that a rock might not be an animal.
The universal negative says something stronger than “rock is not a subgenus of animal,” for we could know this even if there were only one exception. The universality of the negation means that rock and animal are mutually exclusive (there can be no individual that instantiates both); they are essentially contradictory. It is contradictory to say both “X is a rock” and “X is an animal.”
The negation of the universal negative is the indefinite particular affirmative: ‘Some X is Y.’ The particular affirmative may have a definite or indefinite subject. Sentences with definite subjects, such as ‘This man is a lawyer,’ or ‘This man is wise,’ represent straightforward instantiation or exemplification. It is the sentences with indefinite subjects that are of greatest interest, due to their logical relationship with universal statements and the peculiarities of the quantifier ‘some’.
In modern logic, the indefinite particular affirmative is expressed using the existential quantifier ‘there exists’ (∃). This quantifier is placed in a set theoretic context, so we say ‘There exists some x ∈ A such that x is P,’ instead of simply, ‘Some x is P.’ This formalism more explicitly brings out the relationship between the indeterminate object x and its universal, represented imperfectly by the set A. When I say ‘Some man is wise’ (or ‘Some men are wise,’ without presuming number), I use the universal term ‘man’ in the place of an indeterminate particular subject. Modern logical syntax brings this out more clearly, so I should say, ‘Some individual, who is a man, is wise.’
However, the existential quantifier has some inadequacies. First, it reduces instantiation of a universal to membership in a set, an imprecision we have criticized previously. Second, it needlessly introduces an existential declaration when we may be simply considering a hypothetical thesis a priori. In mathematics, there is no distinction between conceptual reality and actual existence, since its “objects” are abstract universals. Thus there is little harm in adding an existential declaration, save the usual confusion resulting from treating universals as concrete objects. Applying such a declaration to metaphysical or physical theses, however, would be problematic.
It is not necessary for the subject to actually exist in order for the indefinite particular affirmation to be true. “Some men are wise” could be a true statement even if no living man is actually wise. The statement means only that there is no logical incompatibility between being a man and being wise, since it is but the negation of the universal negative. As long as it is conceptually possible for an object to both be a man and be wise, the statement holds.
The indefinite particular quantifier ‘some’ can mean any quantity between “one” and “every” inclusive. In other words, it can be anything but “none,” since we are negating the universal negative. Obviously, it cannot be more than “every,” since there cannot be an x that instantiates A yet is not one of the instantiations of A. ‘Some’ therefore means:
{x1} XOR {x2} XOR {x1, x2} XOR {x1, x2, x3}, …, A
‘Some’ encompasses the entire power set of A, except the null set. It resembles the complement of the null set in the power set of A, except we combine elements with the “exclusive OR,” not a set theoretic union. ‘Some’ therefore signifies an undetermined member of this list of possible subsets, but not more than one of these subsets simultaneously.
When the particular affirmative has a plural subject (definite or indefinite), the individuals constituting the subject may act collectively as a subject. For example, in the sentence, ‘These nine men are a baseball team,’ the term ‘baseball team’ is predicated of the nine men considered collectively. If instead we said, ‘These nine men are lawyers,’ there would be no collective subject, but “lawyer” is predicated of each man. English is syntactically ambiguous in this regard with predicate adjectives, since adjectives are not pluralized. Thus we cannot tell whether the sentence ‘These nine men are wise,’ predicates ‘wise’ of the nine men collectively or individually. Languages that pluralize adjectives are better at resolving this ambiguity.
We noted previously that the negation of the universal affirmative is not the universal negative, but the indefinite particular negative: ‘Some X is not Y.’ We can analyze this type of sentence using the same tools expounded in previous examples, since we have already explained what ‘some X’ and ‘not Y’ mean.
We have mentioned two senses in which logical judgments can be opposed to one another: they can be contradictory or contrary. Judgments are contradictory opposites when the principle of contradiction applies to them. This is manifestly the case when one judgment is the negation of the other, but it can also occur when one judgment logically implies the negation of the other. In a word, the judgments are logically incompatible. Contrary judgments entail a stronger form of contradiction. Not only are the judgments incompatible, but they assert diametrically opposing propositions about a subject.
The table below shows the logical oppositions among universal and indefinite particular statements.
| Universal | Indefinite Particular | |||
|---|---|---|---|---|
| Affirmative | Negative | Affirmative | Negative | |
| ‘Every X is Y’ | ‘No X is Y’ | ‘Some X is Y’ | ‘Some X is ~Y’ | |
| Universal Affirmative ‘Every X is Y’ | Identical | Contrary | Compatible | Contradictory |
| Universal Negative ‘No X is Y’ | Contrary | Identical | Contradictory | Compatible |
| Particular Affirmative ‘Some X is Y’ | Compatible | Contradictory | Identical | Compatible |
| Particular Negative ‘Some X is ~Y’ | Contradictory | Compatible | Compatible | Identical |
The pairs of statements indicated as “contradictory” are in each case an affirmation and negation of the same proposition, as discussed previously, so there is no question that the principle of contradiction applies to them. The “contrary” statements are also contradictory, but they are not affirmations and negations of each other. Rather, one logically implies the negation of the other. For example, if “no X is Y,” it follows that “not every X is Y.” In the cases where statements are logically compatible, a universal statement may necessary imply the particular, but the converse does not hold.
The indefinite particular affirmative and indefinite particular negative are logically compatible. This seems strange, since one appears to be syntactically the negation of the other. However, the indeterminacy of the subject makes it possible for the subjects of each statement to be different, so there is no true contradiction. “Some men are lawyers,” does not contradict “Some men are not lawyers,” since the quantifier ‘some’ may refer to any set of men, not necessarily the same set in both statements. Obviously, if overlapping sets were considered, the statements would contradict each other, but then we would have definite subjects, not indefinite ones.
In our discussion of the principle of contradiction, we saw how a negation must be false if its affirmation is true, and so forth. We will now go a step further, and ask if it is absolutely necessary for one of the pair of contradictories to be true (in which case the other is false). This necessity is called the law of the excluded middle, because it excludes the possibility that a proposition could be something between truth and falsity.
Some modern philosophers distinguish the law of the excluded middle from the law of bivalence, the notion that there are only two possible truth values. This distinction is unnecessary, since no truth values beyond “true” and “false” as we have defined them are possible. Either the ontological relationship proposed by the statement is present in some reality, or it is absent. No third thing is possible for any well-defined proposition compared with a well-defined reality. It is conceivable that the truth value is unknown or indeterminate, as is the case with nonsense statements, but no philosopher has coherently posited a third truth value.
In mathematics and computer science, there are many pseudologics that use multiple “truth values,” but these are just generic operations on propositions, and have nothing to do with identifying a correspondence with a given reality. To regard these as real truth values is to confuse syntax with real logic. No philosopher has cogently articulated what the third thing is beyond truth or falsity, other than some arbitrary number, or perhaps some modal qualification of truth or falsity (e.g., probability). If, per impossible, it could be proved that there is a third truth value, then practically all of our deductions would be invalid, including those which form the basis of mathematics and other sciences. Thus the invocation of mathematics to prove the possibility of additional truth values is a thoroughly self-stultifying position.
If there are only two truth values, then the only obstacle remaining to the law of the excluded middle is the possibility that neither of these truth values can be applied. We have already seen that this is the case for nonsense statements and ill-defined propositions, which we have accordingly excluded from consideration. Yet might it not be possible for even well-defined propositions to have no definable truth value? Consider the following affirmation and negation:
Hamlet has a mole on his chin.
Hamlet does not have a mole on his chin.
By the principle of contradiction, the truth of one of these statements entails the falsity of the other, and vice versa. Truth and falsity are only definable with respect to some reality, and here the reality in question is that defined by a work of literature, yet Shakespeare tells us nothing about Hamlet’s physical features. It would seem, then, that neither statement is true or false, even though both are well-defined propositions. The problem is that the literary reality by which we judge truth and falsity is not well-defined on this matter.
Is it at least conceivable that physical or metaphysical reality should also be ill-defined? Most interpretations of quantum mechanics entail some ontological indeterminacy, sometimes clumsily represented by a principle of superposition. While it is irrational to assert that a thing can simultaneously be in contrary states, it seems at least conceivable that the state is not well-defined. In this interpretation, an electron between measurements is in neither spin state (“up” or “down”), for it is only possible to be in such a state when measured (i.e., interacting with something).
In both scenarios, that of literature and that of physics, the paradox arises because the negation is implicitly affirming something else. There should be no difficulty in acknowledging “Hamlet does not have a mole on his chin,” as true, except that we consider the statement to imply that Hamlet has a face without a mole. If we understood the statement as a true negation, saying nothing more than, “I do not allow that the affirmation ‘Hamlet has a mole on his chin’ is true,” then we could accept that the negative statement is true. Similarly, there is no difficulty in saying that “The electron is not in a spin ‘up’ state,” is true, unless we consider that statement to imply that the electron must be in a spin ‘down’ state. In other words, the ambiguity of reality does not entail an ambiguity in logic, if we still define negation to be nothing more than a denial of the affirmation. Thus the law of the excluded middle holds, as a direct consequence of the law of contradiction, in any reality.
All we have said so far holds only if we assume that we are dealing with simple, unambiguous affirmations and negations. There do exist modal propositions for which the law of the excluded middle is not self-evident. For statements about the present or past, there is no obstacle to the law of the excluded middle, but statements about the future, from a human perspective at least, are necessarily statements about possibilities. Unless we beg the question of strong determinism, we cannot consider statements about the future as having definite truth values. It is not necessarily that the future qua future is indefinite, but rather that from our perspective, the future is unknown, potential and indeterminate. It is potentiality and indeterminacy that render the excluded middle inapplicable.
Even when both P and ~P are possible outcomes, we must still admit at least the logical necessity of (P OR ~P) as true. Nor is it at all clear that truth and falsity are not applicable to judgments about the future. After all, every judgment carries at least its own subjective truth value. Further, the fact that we humans cannot know the objective truth or falsity of such statements does not prove that the future has no objective truth or falsity. However, if logic is about the way we can understand the world, the truth value of statements about the future are effectively indeterminate. “Indeterminate” is not really a third value, but rather a way of stating that it could be either true or false. Similarly, when we use indeterminate quantifiers on sets, we are not adding another element to the set.
As I observed in a previous work, the law of the excluded middle might be considered a law of the included middle, since it is consequent to our definition of negation as encompassing all possible states other than that signified by the affirmation. The totality of this inclusiveness is what makes the law hold even in the cases we have described. Those who argue against the law of the included middle are really just arguing against our notion of negation, which we are free to define in the manner stated.
In our discussion of contradictions thus far, we have been concerned principally with negation in the sense of denying the logical content of an affirmed statement. However, we have also noted that it is possible to apply a negative particle (‘not’) to terms in a sentence, signifying the logical complement of the entity represented by the term. Thus ‘non-man’ would refer to any subject other than man, perhaps within some parameters (e.g., we could be considering only animals). ‘Non-X’ does not signify a nullity, but an indeterminate subject spanning all possibilities other than X in some range being considered. The question arises as to how this type of negation, which is really a logical complement, should affect the truth value of propositions.
To distinguish negative terms from the negation of an affirmation, I will use the prefix ‘non-’ for any term that is being negated in the sense of a logical complement. The copula ‘is’ or ‘is not’ signifies if the proposition as a whole is to be understood in the affirmative or negative mood.
| Particular Propositions | |
|---|---|
| Affirmative | Negative |
| (PA1) X is Y | (PN1) X is not Y |
| (PA2) X is non-Y | (PN2) X is not non-Y |
| (PA3) Non-X is Y | (PN3) Non-X is not Y |
| (PA4) Non-X is non-Y | (PN4) Non-X is not non-Y |
Each affirmative and negative pair is contradictory, being the simple affirmation and negation of each other. Further, PA1 and PA2 are mutually contradictory, since ‘non-Y’ is defined to exclude being Y. When I say something is “non-green,” I do not mean that it is some other color in addition to being green, but intend specifically to deny that the subject's color is green. Thus PA2 logically implies PN1, but the converse does not hold, since PN1 could be true even if color were not predicable of the subject at all.
PN2 does not logically imply PA1, since PN2 could be true even if Y were not predicable of X. However, PA1 logically implies PN2, since ‘non-Y’ utterly excludes “being Y.” PN2 and PN1 are logically compatible, since the predicates {Y, non-Y} could all be impredicable of X.
PA3 is compatible with PA1, PN1, PA2, and PN2, since there is nothing preventing different subjects from having the same predicate. Although ‘non-X’ positively excludes “being X,” no contradiction is engendered because the rhema contains the predicate but not the subject. Making contrary or similar assertions about different subjects is no contradiction at all.
Consequent to the independence of statements with different subjects, PA3, PN3, PA4, and PN4 may be considered logically independent of the previous propositions, and they all have the same logical relationships amongst themselves as the earlier propositions did. Thus PA3 contradicts PA4; PN3 and PN4 are compatible; PA4 implies PN3; and PA3 implies PN4.
| Universal Propositions | |
|---|---|
| Affirmative | Negative |
| (UA1) Every X is Y | (UN1) Every X is not Y |
| (UA2) Every X is non-Y | (UN2) Every X is not non-Y |
| (UA3) Every non-X is Y | (UN3) Every non-X is not Y |
| (UA4) Every non-X is non-Y | (UN4) Every non-X is not non-Y |
With universal quantifiers applied to the subjects, we have similar results as before. UA2 contradicts UA1, since the former logically implies UN1. Thus UA2 is not only contradictory, but utterly contrary to UA1. All other relationships among the universal propositions are fully analogous to what has been expounded thus far. Naturally, the truth of a universal proposition logically implies the truth of the corresponding particular proposition whose subject belongs to the universal kind.
| Indefinite Particular Propositions | |
|---|---|
| Affirmative | Negative |
| (IA1) Some X is Y | (IN1) Some X is not Y |
| (IA2) Some X is non-Y | (IN2) Some X is not non-Y |
| (IA3) Some non-X is Y | (IN3) Some non-X is not Y |
| (IA4) Some non-X is non-Y | (IN4) Some non-X is not non-Y |
It is with the indefinite particular propositions that things get interesting, both in the relationships amongst themselves, and in their logical relationships with universal propositions. Most notably, the affirmative and negative pairs are not contradictory, since they do not necessarily have the same subject. There are, however, some logical implications. IA1 implies IN2, and IA2 implies IN1. Analogously, IA3 implies IN4, and IA4 implies IN3.
As established previously, the negation of UA1 is IN1 and the negation of IA1 is UN1. Whence it follows that IA2 is incompatible with UA1 and that UA2 contradicts IA1. However, it does not follow that IN2 is incompatible with UN1, since it is possible for IN2 to be true when IA1 is false. In other words, IN2 could be true when neither Y nor non-Y are predicable of any X. For a similar reason, UN2 is compatible with IN1.
Once again, the third and fourth rows are fully analogous to the first and second. In fact, we can dispense with them altogether as redundant, and produce a consolidated table below.
| Particular Propositions | |
|---|---|
| Affirmative | Negative |
| (PA1) X is Y | (PN1) X is not Y |
| (PA2) X is non-Y | (PN2) X is not non-Y |
| Universal Propositions | |
| Affirmative | Negative |
| (UA1) Every X is Y | (UN1) Every X is not Y |
| (UA2) Every X is non-Y | (UN2) Every X is not non-Y |
| Indefinite Particular Propositions | |
| Affirmative | Negative |
| (IA1) Some X is Y | (IN1) Some X is not Y |
| (IA2) Some X is non-Y | (IN2) Some X is not non-Y |
We may represent the logical relationships among these propositions schematically.
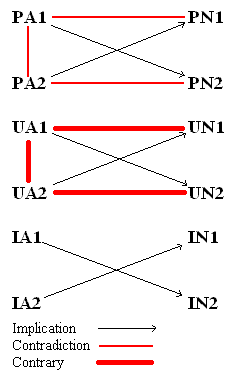
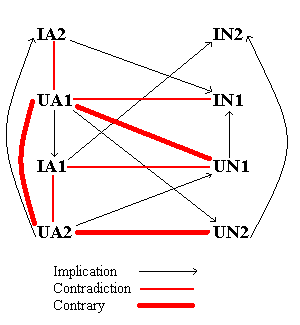
In addition to the relationships depicted, we also know that each universal proposition implies the corresponding particular proposition, as stated earlier. Both UN1 and UA2 are contrary to UA1 since both entail that “No X is Y.”
There may be times when we wish to relate multiple subjects to the same predicate or multiple predicates to the same subject. Such compounds may be represented by a single term when their components are logically dependent. For example, if I say ‘quadrupeds,’ that implicitly contains horses, lions, and tigers, so I do not need to say ‘horses and lions and tigers’. In fact, if I said ‘quadrupeds and horses,’ this would be redundant.
However, when terms are logically or conceptually independent—that is, neither is a genus or differentia of the other—it is necessary to represent them in compound form. Aristotle asks us to suppose that ‘cloak’ meant both “horse” and “man.” The sentence ‘Cloak is white’ would then have only the syntactic appearance of a simple proposition, but it would really represent a double assertion: “Horse is white” and “Man is white.” Looking at quantified forms of this proposition, we find:
‘Every cloak is white’ = “Every horse is white” AND “Every man is white”
‘No cloak is white’ = “No horse is white” AND “No man is white”
‘Some cloak is white’ = “Some horse is white” OR “Some man is white”
‘Some cloak is not white’ = “Some horse is not white” OR “Some man is not white”
Universal propositions are compounded with the connective ‘AND’, while indefinite particular propositions use the inclusive OR (‘A OR B’ meaning “A or B or A AND B”). These results are congruent with a set theoretic description, where the set of all (conceivable) cloaks is the union of the set of all horses and the set of all men. In probability theory, the inclusive OR can be represented as a set theoretic union of possible outcomes. The constructions above also show how we should conjoin compound subjects when they are stated explicitly in sentences: ‘Every horse and man is white’; ‘Some horse or man is white.’ The grammatical conjunctions (‘and’, ‘or’) syntactically couple two nouns, but logically they are coupling the two affirmations represented in the single sentence. There are times, however, when a grammatical ‘and’ really does just couple the nouns, as when we have a collective subject: ‘Laurel and Hardy are a comedic duo.’
The use of the connective OR in compound propositions reflects an indeterminacy between the coupled affirmations, much in the way ‘some’ represents an indeterminacy among possible particular subjects. When I declare the coupled proposition P OR Q, I am not determining whether I am affirming P or Q specifically, but I am only making a more generic affirmation that spans the conceptual range of P and Q. We will further explore the use of the conjunction OR in our discussion of modal logic. The compound proposition P AND Q is simpler to understand, since it is just making two affirmations, P and Q.
When we construct a compound predicate, we seem to run into issues similar to those we encountered for compound subjects. If the compounded predicates are logically independent, they ought to be represented by distinct terms in distinct affirmations. For example, if the predicates “is a man,” “is white,” and “is walking” were all represented by the single term ‘white man walking’, the sentence ‘Socrates is a white man walking’ would have only the syntactic appearance of a single affirmation. It would really represent three affirmations: “Socrates is white;” “Socrates is a man;” “Socrates is walking.” Note that the presence of each modifier signifies a distinct predication of the subject’s being, and this corresponds to a distinct affirmation. However, the presence of the substantive predicate ‘man’ means that the modifiers could instead be predicated of this predicate directly. We have two possible models of the proposition’s predicate relations:
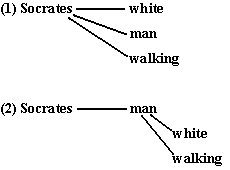
The second model is more in keeping with the grammatical structure of the sentence and our ordinary understanding of such sentences. This predicate structure is permissible only when at least one of the predicates is predicable of another. If the only predicates were “is white” and “is walking,” we would have to say ‘Socrates is white and walking’ (in the sense of the first model), preferably using the conjunction ‘and’ to explicitly show that this is a double affirmation.
As Aristotle observes, there are limits to our choice of predicates to combine. Some combinations could be redundant, corresponding to no truly logical structure. For example, suppose we said, ‘Socrates is a white white man,’ where the second mention of ‘white’ is predicated directly of ‘man’. Applying our two models, we could parse the sentence as:
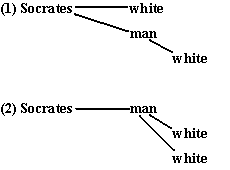
The second case is clearly redundant, as “white” is predicated of “man” twice. The first interpretation makes two assertions: “Socrates is white;” “Socrates is a white man.&Rdquo; These are also redundant, since it is impossible to be a white man without being white. Nor could we allow, as a third possibility, that one “white” is predicated of the other “white” as though they were distinct entities. This is a mere syntactic possibility, and does not correspond to a sound logical statement.
The presence of modifiers logically implies propositions in addition to the central claim of the statement. For example, when we say ‘The tall man is walking,’ the modifier ‘tall’ qualifies the subject, logically implying that “The man is tall.” However, the central assertion of the statement, indicated by the rhema (which grabs our attention, like a rhetor), is that “The man is walking.” The implied assertion that the man is tall is equally essential to the statement, but it is only implied, not explicitly declared. We may suspect that the distinction between the central assertion and implied assertions is purely rhetorical. If that is so, there should be no logical distinction between the statements represented by ‘The tall man is walking’ and ‘The walking man is tall.’ While the statements are logically equivalent in terms of truth values, there is a meaningful distinction between them for the purposes of argumentation. In the first, we assume that the man is tall, and are presently declaring that he is walking. In the second, we assume the man is walking, and presently declare that he is tall. In logical argument, it is important to keep track of our assumptions and the theses we derive from these assumptions, so it is good practice to use a term as a modifier of the grammatical subject or use it as a grammatical predicate, according to whether it is an assumption or a present claim.
In the sentence, ‘The tall man is walking,’ we may say equivalently that “the man” or “the tall man” is the subject of the action “walking,” since the sentence assumes that “the man” and “the tall man” are one and the same. Obviously, “walking” is not predicated of the property “tall;” it is predicated of the subject (“the man”) who is assumed to be tall or identified as tall. There are cases, however, when a predicate can modify the subject modifier by implication. For example, the sentence, ‘This brown hair is dark’ carries the implication that the “brown” of the hair is actually “dark brown.” This implication is not contained in the semantic structure of the statement, but results from the fact that both the semantic modifier and the predicate have a logical dependence when they refer to the same subject. Neither “brown” nor “dark” is a subgenus of the other, but when they refer to the same subject, the latter is understood to modify the former.
When a predicate substantive is modified, it seems that we are defining a more specific universal. For example, the sentence ‘Socrates is a white man’ appears to define a specific kind of man, “white man,” and apply that kind to Socrates. This appearance is even more pronounced in languages that do not use the indefinite article (‘a’). In English, we might say some indeterminate instantiation of “man” is implicitly declared to be white, and then this “man who is white” is rendered determinate by identifying the subject as Socrates. In Greek or Latin, which lack the indefinite article, the universal “man” is qualified by the property “white,” defining a more specific universal, of which Socrates is declared to be an instantiation. Yet even English, with its use of the indefinite article, carries the sense of Socrates being an instance of “white man,” though we can see how English syntax lends itself more readily to describing reality in set theoretic terms rather than explicitly declaring universals.
When an accidental predicate is modified, we also define a more specific universal. For example, the sentence ‘Socrates is walking swiftly’ qualifies “walking” with the quality “swift.” The latter is given an adverbial construction, to indicate unequivocally that the verb, not the noun, is being modified directly. Thus we are identifying a specific kind of walking, “swift walking,” of which Socrates is declared to be the subject. Here even English does not resort to the use of an indefinite article, so we have little choice but to acknowledge that a more specific universal is being declared. This may partially account for why universal accidents (properties) have had broader acceptance among English speakers than universal substances.
Naturally, a subject cannot have multiple predicates coupled by ‘and’ where these would entail a contradiction. However, even contrary predicates can be related to the same subject if they are coupled by ‘or’ understood in an exclusive sense. The sentence: ‘Pet rabbits are black or white’ is free from contradiction if we interpret it to mean: “Pet rabbits are black” XOR “Pet rabbits are white.” The compound statement represents a range of possibilities, and it is such composition with OR and XOR that forms the basis of modal logic, which we shall explore in the next part.
© 2009, 2012 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
| Home | Top |