6. Early History of Logic
7. Terms
8. Aristotle’s Theory of Predication
9. Logic and Metaphysics
10. Syllogisms
10.1 Ontological Classes of Terms in Categorical Syllogisms
10.2 Quantification of Categorical Syllogisms
10.3 Modal Syllogisms
10.4 Transitivity of Subordination and Superordination
10.5 Rules for Syllogisms and Extension of Terms
10.6 Moods or Modes of Syllogisms
Zeno of Elea is widely regarded as the inventor of logic, since he was the first to explicitly identify what we might call rules of inference. Naturally, important elements of logic preceded Zeno. Rhetoricians such as the famed Protagoras understood the subtleties of disputation, including dialectical argument. The study of grammar had long been considered essential to an Athenian education, and as we saw at length in Logic and Language, the syntax of language often reflects a logical structure according to the understanding of its users. Anyone who speaks human language practices logic all the time, often effortlessly and without awareness that he is performing a special act. Many rules of logic have been internalized as rules of grammar: e.g., if a verb is plural, the subject must be plural; every sentence must have a verb; there can be no adjective without a noun; and so on. Once fluent in a language, we may forget the rules of grammar school, yet apply them anyway in our speech, since we have internalized the logic that underlies them. Zeno is considered the founder of logic because he is the earliest known philosopher to state the rules of logic explicitly, where others had practiced them intuitively.
The explicit statement of rules of inference that followed from a priori necessity allows us to distinguish logic from rhetoric, which may also use intuitive probabilistic arguments or arguments of persuasion. We may consider modal logic as part of logic, though it does not involve necessity in the dictum, since its inferences are no less necessary. The probable arguments at the disposal of the rhetorician, by contrast, extend to appeals to particular epistemologies that let us judge a fact to be more or less likely. For example, a rhetorician may argue that it is probable that a man committed murder, since the accused was the only person present with the victim. Such an argument requires us to have an epistemic view that regards other possible explanations as unlikely. With true modal logic, by contrast, we do not rely on subjective assessments of probability, but on what is a priori possible or impossible. Suppose A is possible, and that B is not possible. Then we can infer, as a matter of logical a priori necessity, that ¬B is necessary, A ∧ (¬B) is possible, and so on. (¬ = ‘not,’ ∧ = ‘and.’) The principal objective of logic, in its origins, was to identify which arguments are always valid, not necessarily which judgments are always true. Developing arguments that are unfailingly valid enables us to identify a structure of logical connections among judgments, before we even examine the real world. The power of logic is in its a priori necessity, and those who would make it an a posteriori science eviscerate it of its strengths, and render the use of language—any language—intellectually unjustifiable.
Explicit statement of rules of inference also helps us distinguish logic from grammar, as the logical structure implicit in syntax is now brought forward, and we are able to judge whether or not a linguistic usage is logical. The distinction between logic and language enables us to free ourselves from linguistic custom, and we may recognize the pseudo-paradoxes of the sophists as mere wordplay that takes advantage of the imprecision and occasional illogic of ordinary language. This recognition of the limitations of ordinary language may lead us to impose a more technical vocabulary and syntax on our language when engaging in dialectical argument. The first steps toward this end would be made by Plato and Aristotle.
Although Zeno’s logic was an important step toward freeing Greek philosophy from the domination of rhetoricians (the sophists), it was exceedingly rudimentary, to the extent that it yielded pseudo-paradoxes that brought discredit on logic. Zeno’s famous paradoxes, such as that of Achilles and the tortoise, gave results so wildly counterintuitive (we all know that Achilles must pass the tortoise) that it effectively made logic another sophism, a mere rhetorical device for winning arguments. Indeed, Socrates (as represented in Plato’s dialogues) frequently accuses the sophists of using chop-logic
to prove any point they wished, a criticism Aristophanes extended even to Socrates himself. Even today, it is common to use ‘logic’ in this equivocal sense, where one presumes to prove a priori what is certainly known as false from experience. Such logic is often parodied in popular science fiction, whenever some ostensibly logical computer, robot or alien is led to some self-contradiction or other paradox. Zeno’s own school applied crude logic to disastrous effect in metaphysics, where Parmenides reasoned that there could only be Being and not Not Being, leading to his conclusion that all motion and change is an illusion. From an early stage, the failure to ground logic in a sound ontology could lead to disastrous results. Parmenides’ metaphysics is so fantastically counter-empirical that many have supposed he did not really mean it, or was merely conducting an intellectual exercise. Aristotle, however, leaves little doubt that the Eleatic school did take this seriously, forcing him to do likewise. Given the other fantastic results of early attempts at philosophy (e.g., the Pythagoreans), we should not be surprised that this theory was held in earnest.
Socrates did much to confute the sophists, without achieving anything resembling a system of logic. Naturally, he practiced logic that is implicit in the use of language. However, he did not, as a rule, allow himself to be caught up in linguistic entanglements. He accomplished this through a method of argumentation where he assumed what was believed by his adversary, and followed its consequences until it led to a contradiction. Such a method assumed rules of inference, but only of the most basic sort that even an adversary would accept.
Plato did little to develop a system of logic, as far as we know, yet his precision of thought cannot be accounted without admitting that he must have internalized some sophisticated rules of inference. His Cratylus dialogue gives evidence that he was aware of the logical structure and limitations of language, and he saw the advantage of imposing a more technical vocabulary in philosophy. The most famous is his idea, which originally meant the shape of an object, but has now come to have the Platonic significance as its primary meaning. Still, Plato did nothing to impose a technical logical syntax, nor to explicitly state the rules of inference.
Logic as we know it really began with Aristotle, that encyclopedic intellect whose studies embraced the ontology and semantics seemingly underpinning a logical system. While his works on natural philosophy have been supplanted by new models and theories, his logic still looms large over the Western mind, despite the best efforts of modern logicians to efface his work with their formalizations. Aristotelian logic is logic, in the common sense notion of the term, with its principles of non-contradiction and the excluded middle, its rules of inference and syllogism, its notions of affirmation and negation, truth and falsity. Aristotle’s logic still resonates with us because it is the logic we actually practice when we reason. Even when we reason about the various calculuses and symbolic ‘logics’ we have developed, we use Aristotelian logic. Aristotle did not invent this logic; it is accessible to every intellectual being from a priori principles, concepts and intuitions. What he did was state its rules explicitly, and impose rules of syntax on dialectical argument, which continued to use ordinary language though in a highly technical way. He also analyzed a priori ontology to consider all possible categories for the terms of logic. Contrary to some modern detractors, Aristotelian logic does not incorporate metaphysics. It does not assume potentiality and actuality, matter and form and the like. It does take the a priori categories of substance and accident, universal and particular, but does not prejudge the reality of these as distinct entities.
Modern logic has pretended to remove ontology from logic by completely formalizing syntax, and making rules of syntax to be rules of inference. This succeeds in removing ontology from logic only if we consider our sentences as strings of symbols signifying nothing. As soon as we admit that our symbols and syntax are just tools for representing a conceptual logic, the question arises: what concepts does our logic treat? Perhaps the most general answer we can give is: entities considered a priori. These entities must be at least part of the scope of logic, or we really are talking about nothing. It is not necessary for these entities to actually exist, but it must at least be conceivable for them to exist in order to be intelligible. The intelligible is the domain of logic, which gives rules for building our understanding. The symbols we use to represent intelligible entities represent terms, which are necessarily the basis of any logic that is not merely syntax without intelligible content.
In Logic and Language, we considered the different ways words could represent entities considered conceptually. We saw that some words, nouns, name entities, while other expressions, which we may call verb phrases or rhema, call attention to a mode of being. In order to articulate a coherent logical judgment, we need both a noun to act as subject and a rhema to denote the mode of being that is somehow affirmed or denied of the subject. We need both of these components to make a statement that is logical, that is, a statement that says something about the mode of being of some entity, considered a priori. Without this modicum of ontological content, logic would be just a symbolic game not signifying anything, and would have no reason to prefer one logistic over another. Since logic is eo ipso concerned with ontology, it could matter whether our subject and rhema represent universals or particulars, substance or accident. We explored the possible permutations in Logic and Language.
Taking a simple proposition, ‘S is P,’ we note that the rhema ‘is P’ consists of two components, the copula ‘is’ and the predicate P. The predicate represents some entity, and the copula declares the mode of being by which the predicate entity is related to the subject entity. Although not all languages use a copula, it is always implied, since the declaration of a sentence ‘S-P,’ understood as affirming or denying something, necessarily declares something about the ontological relationship between S and P. This does not mean that ‘is’ represents a third thing, as though being itself were an entity, but a declaration of being is essential to any statement, so if we incorporate the copula as part of the predicate, we must make clear whether the mode of declaration is affirmative or negative, or some other mode. We can avoid using ‘is’ as a separate word, but we cannot avoid conveying its meaning when we declare a statement. The copula is more essential to a rhema than a predicate, for we could have simple ontological statements, such as ‘S is’ or ‘S is not,’ meaning ‘S exists’ or ‘S does not exist.’ These statements will not concern us for the moment, as we will only treat statements with a subject and predicate. The copula may be considered either as distinct from the predicate or incorporated into it.
When we are considering statements that compose a logical argument, namely propositions, which can be affirmations or negations, we may consider each sentence as representing a premise or a conclusion drawn from premises. The rules for drawing conclusions from premises are rules of inference. The most basic of these do not depend on the categorical content of the subject or predicate. The subject and predicate of a premise or conclusion are called terms, or `ορος in Greek, which means the limit (much like terminus in Latin). It is a limit of either the beginning or the end. The subject and predicate are the beginning and end of a judgment not only in terms of their syntactic position in a sentence, but also with respect to the ontological relationship declared by the statement. A proposition affirms or denies the presence of an ontological relationship between the entities signified by the subject and the predicate. The two terms delineate the bounds within which being is considered. In other words, the significance of ‘is’ in ‘S is P’ depends on what S and P are. In the sentence ‘Socrates is a man,’ ‘Socrates’ refers to an individual substance while ‘man’ signifies a universal substance or species. The copula ‘is’, the essence of the affirmation, there signifies the presence of an ontological relationship between an individual substance and a universal substance, which is that of instantiation. If the sentence instead were ‘Socrates is white,’ where ‘white’ signifies some universal accident or property, the ontological relationship declared by the statement would be that between an object and a property, or exemplification. The subject and predicate, in each case, delineate the bounds in which ‘being’ is declared by a statement. This ontological content is limited not only by the categorical content of each term, but even by its most specific content. The relationship between Socrates and white
signified by ‘Socrates is white’ is not identical with the relationship between Callias and tall
in ‘Callias is tall,’ though they are similar in kind (exemplification). This is proved, for example, by the fact that it is possible for one relationship to be actually present while the other is not. Even in cases where there is logical dependence, we can see the relationships as distinct. If Socrates is a man
is true,[1] then it is also the case that Socrates is an animal.
Yet the relationship between Socrates and man
is not identical with that between Socrates and animal
since it would be conceivable for an entity to be a man without being an animal, and Socrates’ rationality is essential to his being a man, but not to his being an animal. For any two conceivably distinct entities, we may conceive of their relationship a unique aspect that distinguishes it from other ontological relationships.
As mentioned, we can discern some rules of inference without reference to the specific or even categorical content of terms. This type of logic is truly formal, since it depends on the form and not the content of an argument. In classical logic, the following terminology was used to identify the inferential relationships among terms. All inferences were modeled as syllogisms, where a conclusion is inferred from two premises. The middle term (M) is the term that appears in the two premises but not in the conclusion. The minor term (S) or last term is the term that appears first in the conclusion (i.e., as the subject), while the major term or first term (P) is the term that appears second in the conclusion (as the predicate). A syllogism using such terms could have this form:
Major premise: M is P
Minor premise: S is M
Conclusion: S is P
If we regard the copula ‘is’ as incorporated into the predicate, we can regard the ‘is P’ in both the major premise and the conclusion as having identical signification. In this case the syllogism is valid only if the minor premise is an identity. For example:
White is a color.
Socrates is white.
∴ Socrates is a color.
Since Socrates and white are categorically distinct, ‘color’ cannot be predicated of them in the same way. Socrates exemplifies the property of color, while white is a kind of color. The syllogism is valid, but we must make use of our a priori knowledge of the ontological square in order to know in what sense P is predicated of S.
In cases where the minor premise is not an identity, such as the example just discussed, the copula cannot be semantically incorporated into the predicate, though we may do so syntactically at our own peril. We need to be aware of the different senses of ‘is’ in each of these predicates. Thus, in order to construct any but the simplest of syllogisms, we need to be aware of the fundamental ontological class of each term.
Aristotle and his successors often did not clearly distinguish linguistic objects from the concepts they signify, since in practice our words act as surrogates for concepts. Lukaciewicz, the great modern interpreter of Scholasticism, held that terms were not ideas, notions or concepts. It is tempting to reduce terms to their grammatical representations, since sentences have a grammatical subject and predicate. If we may borrow a notion from modern logic, we may say that terms are interpreted linguistic objects, understood as representing conceptual entities. We have seen from our consideration of even an elementary syllogism that term logic is ontologically laden. As noted previously, this incorporation of ontology into logic does not prejudge metaphysics, but allows all conceivable metaphysical theories that have no a priori internal contradiction.
Term logic is of particular interest when the terms are universals. For example, consider this syllogism:
Men are bipedal.
Socrates is a man.
∴ Socrates is bipedal.
The syllogism holds only if the major premise is understood universally: the universal man
is essentially bipedal, or all conceivable men are bipedal. Both these possibilities are logically equivalent, as we showed in Logic and Language, discussing modal logic. If it merely happened to be the case that all actual men are bipedal, the syllogism would also hold, though this would now be an a posteriori inference. In any case, the major premise may be stated in the form ‘All A’s are B’s,’ where A and B represent entities. Inferences, by contrast, have full propositions as their variables. ‘If A then B’ means if A is true, then B is true, so both A and B must be propositions, not mere terms, since only propositions can have logical truth or falsity.
Synthesizing what we have said about universal premises and inferences, we find that All A’s are B’s
is logically equivalent to ∀c(Ac) → (Bc). That is, if c is A, then c is B. Here A and B are predicate relations. This formulation shows the equivalence between term logic and modern predicate logic, only if we allow c to be every conceivable entity. If it is restricted to only actually existing entities, predicate logic fails to capture the notion of universals, not because it is impossible to construct a predicate logic with true universals, but because logicians have chosen to confine themselves to Russell’s theory of reference and a set theoretic account of universal classes, effectively presuming a priori that there are no universal entities, only predicates that apply to all objects in a set. We see that there is no necessity to impose this limitation on predicate logic, so one of our aims will be to correct it so that it can give as full an account of universals as term logic.
For Aristotle, all premises are attributions, where the essence of some predicate is ascribed to a subject. This is a sound assumption for simple propositions, but we may find the rules of inference for these statements difficult or even impossible to apply to more complex statements. Restricting our scope to simple propositions, we find that there are different types of attribution depending on the ontological category of each term. When a universal substance is attributed to a particular substance, the essence of the universal is also the essence of the particular, so we may say that the particular, in essence, is the universal. A different sort of attribution occurs when we predicate an accident of some substance. The accident may modify the essence of a substance, but it is ontologically dependent on its subject, and it is categorically distinct from its subject in a way that makes a strong identification of essence impossible. For example, consider the statements, Socrates is a man,
and Socrates is white.
In the first case, the essence of man is to be a rational animal, and Socrates is a rational animal, so the essence of man is directly predicable of Socrates. In the second case, white is a color that reflects all or most visible light frequencies.
Socrates himself is not a color, so the essence of white is not predicable of him in the same way that the essence of man is predicable of him. Thus we might say that Socrates has the attribute of being white, but he is not a white.
Some modern philosophers have tried to obscure this distinction by describing universal attributions as properties, so we could say, for example, that Socrates has the attribute of being man,
as if this were no different a predication from having the attribute of being white. This reduction is possible only if we assume that man
cannot be a substantive, an assumption that has no place in a priori logic, since its negation involves no self-contradiction.
In Logic and Language, we explored all the different possible attributions in simple propositions, based on the fundamental ontological categories of the terms. Instead of saying, Man is bipedal,
standard universal affirmations are of the form ‘All men are bipedal,’ describing universals at best indirectly through their instantiations. If by ‘all men’ we only mean every actually existing man, we cannot establish the true universal proposition: Man is bipedal.
It would be necessary for every conceivable man to be bipedal in order for this predicative relationship between universal essences to hold as an a priori truth. The unfortunate custom of classical philosophers of phrasing universal affirmations and negations as statements about particulars (‘All A’s are B’ or ‘No A’s are B’) has lent itself to elision toward dispensing with universals altogether, and restricting the scope of the universal quantifier ‘all’ to actually existing referents. This makes possible a set theoretic account of universals and particulars, but only by distorting the notion of universal
and moving logic into a posteriori metaphysics. The universals
of set theory are in fact just groups of individuals, and the universal quantifier
cannot take us to the conceptual essence of a class if it is confined to actually existing objects, for there is no way to distinguish between essential and accidental attribution. No man alive today speaks Etruscan, but it would be an absurdity to infer from this that speaking Etruscan is contrary to the essence of being man, so that a priori, If it speaks Etruscan, it cannot be a man.
If we are truly to make statements with the force of logical necessity, and not mere empirical observation, we must consider all conceivable instantiations of a universal, which we can do by understanding the essence of the universal conceptually, rather than perform an infinite thought experiment. In actuality, set theory does make use of true universals, such as the concepts of rational number, integer, etc., even though mathematicians may insist on the clumsy forced definition of these concepts in terms of groups of objects. We will explore the role of universals in set theory much later. For now, we merely note the necessity of a universal concept in order to make practicable any statement regarding infinitely many conceivable instantiations.
A problem that is fundamental to term logic is interpreting the copula ‘is’ in ‘S is P.’ There are two theories on this matter. The first, called aspect theory, interprets ‘S is P’ as S is existent as P.
Thus a simple proposition contains a dual claim: (1) S is existent; (2) P is predicated of S. Thus, for the statement Socrates is a man,
to be true, Socrates must exist. This seems intuitive enough, as it matches our interpretation of ordinary language. If someone said ‘Socrates is walking,’ knowing that Socrates did not exist, we would call that person a liar. The being of the accident is utterly dependent on the being of the subject, so the predicate attribution cannot possibly be true if the subject does not exist. It would seem, then, that accidental attributions are at least logically implicative of the existence of the subject. However, when we are dealing with abstract a priori concepts, such as Lilliputians are tiny,
the subject need not be existent for the statement to be true, if we understand the abstract or fictional context being considered. Further, the statement A dodo is a bird,
might be considered true even if dodos do not exist or never existed, as long as the definition of dodo
contains the differentiae of bird.
These latter considerations may lead us to adopt a copulative theory of predication, where ‘S is P’ simply means P is predicated of S, and carries no existential claim about S. The sentence ‘S is P’ in aspect theory would be equivalent to (‘S is P’ AND ‘S is’) in copulative theory, where ‘S is’ is a declaration that S exists.
Allan Bäck has conducted an extensive study on the theories of predication held by philosophers in the classical tradition.[2] He finds that the Stoics and the Aristotelian interpreters Philoponus and Theophrastus likely held the aspect theory, while Avicenna unquestionably did hold aspect theory. St. Thomas Aquinas and his school, by contrast, held to the copulative theory, which was also likely held by Plato and his school. Aspect theory seems most consistent with the thought of Parmenides, who seems to have regarded ‘S is’ or ‘S is P’ as implying that S exists. Yet he also regarded ‘S is not’ as implying S does not exist. His apparent use of aspect theory allowed him to arrive at the paradox that plurality cannot exist. Suppose S is P and S is Q, where P and Q are distinct predicates, so that there is plurality in S. Since Q is ‘not P,’ it follows that ‘S is not P,’ so S is not, according to Parmenides, but there cannot be anything that is not. Aspect theory alone does not give us Parmenides’ paradox, since it is also necessary to confuse the ‘not’ of negation with the complement of a term. Much less do we necessarily arrive at his monism, where only the One exists. As Bäck points out, we might have also arrived at a sort of atomism, where each thing simply is, without predication, or even a predicated monism, where the One may have properties that do not contradict each other.
Bäck observes that aspect theory seems to conflate the ‘is’ of predication, existence, identity, and the constitutive ‘is.’ The ‘is’ in ‘S is P’ signifies both predication and the existence of S, and may signify identity when S and P are categorically similar (e.g., John is Mr. Roberts). This conflation of functions, while convenient, and reflecting a real logical implication, results in equivocation when we have ‘S is not P,’ since this could mean either S is not existent or P is not predicated of S. ‘Robin Hood is not an archer’ could be considered true on account of Robin Hood being non-existent, for example. Similarly, the ‘is’ of instantiation is not distinguished from the ‘is’ of superordination (relating subgenus to genus). Modern logicians such as Frege and Russell have sought to resolve this ambiguity by assigning different symbols for different aspects or functions of ‘is.’ Thus each symbol is univocal, but perhaps at a price, for we seem to obscure what these various functions do have in common, a fact intuitively recognized by humans, who have constantly lumped them together with a single verb: ‘to be.’ If we are to grasp Aristotelian predication, we must come to grips with what it means to be.
Aristotle uses ‘being’ (to on, το ον) as a substantive, meaning ‘that which is.’ He divides being into categories, not to give different meanings of ‘being,’ but to give a list of the types of objects that may be. When he gives the ontological square, he classifies entities (things that are) according to their predication relations. He distinguishes ‘being said of’ and ‘being in a subject’ as two distinct predication relations. In our discussion of the ontological square (Introduction to Ontological Categories, Part I; Logic and Language, Part II), we expounded all the different predication relationships among these basic four categories. We summarize these below:
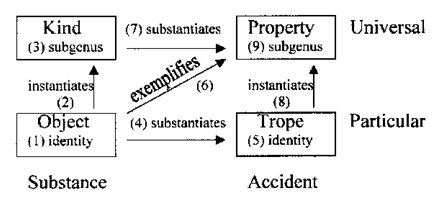
We note that universals can be related to one another not only by identity, but also by being a subgenus of the other. This is similar to what C.S. Peirce called subsumption, except Peirce tried to expand the concept so that every proposition could be stated as a subsumption relation, a calculus we will later criticize. The converse of subsumption may be called superordination, which is distinct from instantiation. ‘Socrates is a man’ relates instantiation, while ‘Man is an animal’ relates subordination. We cannot simply infer ‘Socrates is an animal’ by some transitive property of being, since ‘is’ has a different signification in each sentence. However, as shown in the Introduction to Ontological Categories, Part I, such an inference is sound because in both cases the essence of the more universal entity is conveyed to the lower (see also Logic and Language, Part II).
Predicate entities may be defined per genus et differentia. Thus we can say that S is P and P is G—D. The ‘is’ in the second expression is practically an identity, except it is not a renaming, but rather a declaration of the essence in terms of a more generic substance. If we intend P is G—D
as a definition, then we can make a straight substitution of G—D for P:
Man is a rational animal = Man is subsumed by animal and characterized by rational
P is G—D
Socrates is a man → Socrates instantiates man → Socrates instantiates what man is subsumed by (as proved in Intro. to Ont. Cat.) → Socrates instantiates animal
(S is P) AND (P is G—D) → S is G—D
Suppose we did not intend P is G—D
as a definition, but as an ordinary statement, e.g., Man is a bipedal animal.
It would nonetheless follow that Socrates, or any other instantiation of man, must be a bipedal animal.
In all the various kinds of predication shown in the ontological square, what they have in common is that the ‘is’ in ‘S is P’ signifies that the essence of P is in some way found to pertain to S. By the ‘essence’ I mean nothing mysterious, only that which makes a thing what it is, or the conceptual entity signified by the term. Universals are their essences, as a matter of identity, since they are defined conceptually. Particulars can have the essence of a universal, yet they also have a thisness
that distinguishes them from other instances of the same universal. A particular is the universal, or rather an instance of it. The essence of the universal, which is the universal, pertains to the instance, which shares everything of the universal, yet there is more to its being than the universal.
Universals themselves may be related by superordination and subordination. A subordinate universal fully contains the essence of its genus, yet there is more to its being than the genus. Since subordination fully conveys the essence of the higher to the lower, we can see why subordination and instantiation may be linked inferentially. For example:
Man is an animal (subordination) → Man has the essence of animal
Socrates is a man (instantiation) → Socrates has the essence of man
Since the essence of the universal man
is the universal man, we rightly infer that Socrates is an animal,
i.e., Socrates has the essence of animal. This common sense inference is considered problematic by modern logicians, as if that were an indictment of common sense rather than of their system. Indeed, if we cannot be certain of simple inferences as these, there is no reason we should have any faith that mathematicians, logicians, and scientists are able to reason soundly on more subtle matters. A common trope in modern logic is to ask us to doubt what is obvious and accept what is far more complex.
Essence may be conveyed in a different way from accident to subject. The essence of an accident may modify the essence of its subject, but it may not be directly predicated of the subject. For example, ‘A sphere is round,’ means that it belongs to the essence of a sphere to be round, or rather that the essence of round is part of the conceptual composition of a sphere, yet the essence of round, which is round (the essence of a universal is the universal), is not the essence of sphere. There are some similarities with the instantiation and subordination relations, however. The essence of the predicate pertains to the subject, yet there is more to the subject’s being than the essence. Again, we can see why we would use the same linguistic form of predication for this relation, changing only the category of the terms (typically using modifiers instead of substitution for the predicate). The a priori difference between substance and accident is explained in the Introduction to Ontological Categories (Parts I and II). We note that a subject is not an instance of its accident, nor a more specific form of the accident. The something more
in its being beyond the essence of its predicate is not thisness,
but being the substance of the accident. ‘S is P’ may be read, ‘S is the substance of P’ or ‘P subsists in S.’
An individual substance may exemplify a universal accident. This means it instantiates some species that is the substance of the accident. We could equivalently say that an instance of the accident subsists in the object, without invoking a universal substance. Alternatively, we could say the property subsists directly in the object, without invoking individual accidents. In this last account, which is property-object ontology, exemplification is the only predicate relation. Since we are dealing with a priori concepts, we do not need to prejudge the existence or non-existence of entities in any of the four ontological classes, so we retain them all, with all their types of predication.
It remains to examine ‘is’ itself, not merely as a link between two terms, but as significant in itself. When we affirm simply X is
(or X exists
), we refer simply to being, which is not a category or predication, but a more primitive notion. Being is essential to defining predications, as a predication shows the way of being or kind of being of the subject (and predicate). Hence, Socrates is a philosopher
tells us that philosopher
is the kind of being that Socrates is; Socrates is a wise
tells us how Socrates is. The copula ‘is’ (ens copulae) grammatically links subject and predicate, and its position as neither subject nor predicate reflects the reality that being underlies both, and is what binds them together.
In modern predicate logic, it is common to incorporate being
explicitly into the predicate. Thus, ‘Socrates is a philosopher’ or ‘P(s)’ would have ‘Socrates’ (‘s’) as the subject, and ‘is a philosopher’ (‘P’) as the predicate. This semantic shift seems to eliminate the need for universal substances, as philosopher
is replaced by the apparent property being a philosopher
or being philosophical,
defined by some set of attributes. The reality of universal substances is certainly debatable, even in a classical context, but the resolution of this metaphysical question does not rest on formal syntax. Incorporating being
explicitly into the predicate, whether as being a philosopher
or being one who loves wisdom,
does not change the ontological category of the entity signified, since all entities, substances or accidents, are modes of being, as being transcends the categories.
The ‘is’ in ‘Socrates is wise’ and ‘Socrates is a philosopher,’ the ens copulae, is very different from the is in ‘Socrates is,’ meaning Socrates exists.
The latter ‘is’ is not a mere copula, for it affirms (ontologically) the real being of Socrates, not as though being
were something separable from the subject, nor even an action that the subject does. Being is simply the reality of the subject in question. We could not regard being as a genus or predication except equivocally. Socrates is wise
only accidentally; in general, there is more to the subject than its predicate. Socrates is,
on the other hand, is a positive statement of reality, and the ‘is’ is unique to Socrates, signifying a being that is exactly co-extensive with the subject.
In our discussion of Aristotle’s model of predication, we have repeatedly made reference to being and existence. It would seem that we are incorporating metaphysical assumptions into our logic. To guard against this possibility, we should take care to distinguish logic from metaphysics, as regarding being.
The very name ‘metaphysics’ comes from the title applied (perhaps posthumously) to a work of Aristotle, ‘μετα το πυσικον,’ or beyond the physics.
The original signification of this title may have been simply to indicate that this was the work in the Aristotelian corpus that came after the Physics. Indeed, extensive excerpts from the Physics have been copied into the Metaphysics, so there is considerable overlap of content. The matter is further confused by the fact that the Physics contains discussions of potentiality and actuality, being and non-being, as well as other topics we might consider metaphysical. Indeed, Feijoo may have put it best when he said that Aristotle’s physics should be interpreted as philosophy of science, not as empirical science itself.
Modern thinkers, implicitly or explicitly, tend to distinguish physics from metaphysics as between the empirical and the non-empirical. Those who adopt scientism will deny we can know anything about the non-empirical world (i.e., the world beyond the reach of empirical investigation), and therefore deny metaphysics of any sort. Those who do admit a metaphysics may see it as an ontological substratum underlying empirical reality, or perhaps as a statement of formal generalization about existing objects. Both of these perspectives contain aspects of what Aristotle considered metaphysics.
Aristotle called metaphysics first philosophy,
which was an inquiry into the most general characteristics of reality, transcending individual sciences. Since first philosophy dealt with the most general aspects of reality, all the other sciences would draw upon it in some way. It is unsurprising, therefore, to find a discussion of being and non-being in the Physics. Earlier philosophers had attempted to give a general account of reality by reference to some natural substance such as water or fire, or musical harmonies, or mathematical objects. All these philosophers made the same error of mistaking their particular science (physics, chemistry, music, mathematics) for a generic first philosophy. Modern scientists commit this same error, as when biologists pretend to explain everything (from astrophysics to human history) in terms of evolution, or when physicists regard everything as particles or fields, or computer scientists think ideas are just bits! In earlier eras, it was pretended that mechanism accounted for everything, and even human beings were no more than complex machines. The humanist-scholastic debate and Galileo’s battles with natural philosophers were in many respects little more than academic turf wars, with each side thinking its specialization was the higher or first philosophy. In this context, it is unsurprising that today’s scientists are generally irreligious. Practically all academics adopt the habit of seeing everything in terms of their discipline. Those trained in a field where all knowledge comes from sensory observations may be led to dismiss a priori that which cannot be observed by the senses, or will not submit to a controlled experiment.
In terms of epistemology, Aristotle recognized that human knowledge begins in the empirical realm. Before one can approach metaphysics, one must first identify the fundamental principles of each science. We do this by applying these principles to our observations, establishing them empirically, and then by classifying these principles conceptually, using logical reasoning. After we have done this for many sciences, we can begin to discern principles that are common to all the sciences, however disparate. These principles constitute our system of metaphysics, or first philosophy.
All science is concerned with knowledge of things that are, so metaphysics ought to concern itself at least with ‘being’ in the most generic sense. When we study entities, we consider them as objects of thought, and ascribe to them properties in thought. Thus to be
in the most generic sense need not specify existence, but only means to be a subject of thought or to have properties. Being may be considered a priori, not just a posteriori, and it is in the former context that Aristotle gives substance a logical (and seemingly grammatical) criterion: it is always a subject, never a predicate. This is a practical necessity, since a substance cannot be formally defined except by its properties. Any term we give to a substance would just be a meaningless tag or label, unless we understand the substance to be circumscribed by the manifestation of certain properties. We use properties to define where one substance ends and another begins (both universals and particulars). We cannot think of substances without recourse to accidents, so our intellectual or scientific activity presumes these highest categories.
Logic, Nicholas Capaldi remarks, is the structure of thought and speech regarding our experience.[3] It gives form and rules to the epistemologies and languages with which we analyze the world, subjecting them to criteria of validity. Recapitulating the definition of John Duns Scotus, logic studies principles of thought about the world, while metaphysics studies fundamental principles of the world itself. If thought or speech about the world were identical with the real world, there would be no distinction between logic and metaphysics. However, Aristotelians must deny this identity. For example, as Capaldi notes, universal terms do not directly refer to independently existing forms (as Plato had held).[4]
There are two parts of logic: (1) the structure of language, or syntax, and (2) the semantics of how we abstract universals from experience. For St. Thomas Aquinas, these two parts were continuous, while William of Ockham, who denied the metaphysical reality of universals, also denied there was any semantics in logic. This reduced logic to mere syntax. Russell, Peirce and others helped restore semantics to logic by building a theory of reference, yet this kept the two parts of logic separate and independent. As we have seen, our choice of logical rules of syntax are informed by the categories of our terms. Modern logic hopes to avoid this necessity by collapsing universals into attributes or objects. Thus we can neatly distinguish form from content, but only by assuming an impoverished ontology a priori. What is more, modern logic must ignore the copula or incorporate it into the predicate, or reduce it to just another symbol. The semantics of modern logic is far from complete, for it dismisses out of hand as impossible entire classes of coherent thoughts and arguments that men have actually held.
Notwithstanding their contention that ontology has no place in logic, modern logicians do have a notion of existence built into their system. They may try to give existence a purely syntactic function, but in order for their logic to be intelligible, they must ascribe some ontological significance to existence.
Frege held that properties affirmed of a concept are not characteristics that compose the concept, but properties of the things that lie beneath the concept. In other words, he assumed a priori that only particular objects have properties, and that there are no universal substances. For example, when we say, A leopard is a spotted feline,
the (universal) concept leopard
is not composed of spotted
and other characteristic properties, but we only affirm that individual instances of leopard
are spotted. While spotted
is not related to the concept leopard
(note that Frege assumes universals are concepts only, and not entities signified by concepts) as a part to whole, it is a constituent in a non-extensive sense. Further, Frege’s restrictive interpretation of universal predications denies what many people actually intend by such statements. When I say, Man is rational,
I do not primarily intend to make a comment about actually existing individuals, but make a broader statement, encompassing men who may never exist, and saying something about the essence of what it means to be man.
This universality is even more evident with abstract terms, as in Wisdom is good,
where I ordinarily do not have any particular instance of wisdom in mind, but intend the universal. This a perfectly coherent a priori position, yet Frege dismisses it out of hand by insisting that all properties must belong to particular objects only. He already incorporates metaphysics (Ockhamism) into his logic.
This is not the least of Frege’s blunders. He defines existence as the negation of O, where O is a proposition of the form, There is no rectangular triangle.
This clearly defines the more primitive in terms of the less primitive, as the assertion O is intelligible only if we have some notion of existence in the first place. Since Frege wishes to make formal syntax more fundamental, and he understands negation as a formal syntax, he decides to make negation more fundamental than existence. Negation, as we have seen (in Logic and Language), is a denial of being, not necessarily in the sense of actual existence, but in whatever mode the primary assertion is affirmed. Frege, absurdly, would pretend to ignore ontology when discussing existence, which is but one mode of being.
He defines O in terms of logical cogency; that is, O is based on a statement of the form X is P
where P cannot apply to X. This statement of impredicability is O, and the negation of O is a declaration of existence. It is clear that Frege’s existence
is really just a priori possibility. Given his mathematical background, we should be unsurprised that Frege fails to distinguish between conceivable and actual existence, as no such distinction exists in abstract mathematics.
From what we have said, Frege’s existence
really means sometimes true;
that is, x with property P
exists if P(x) is true for some x. There is no notion of x exists
simply and absolutely; existence is defined in relation to some predicate. Even if this were sound metaphysics, there is no reason to build this metaphysics a priori into our logic, as other systems are possible. Frege’s definition of existence
is fine if we do not assume it is real metaphysical existence, but recognize that it is just a formal definition in terms of logical syntax. What is problematic is when logicians presume to have reduced real metaphysical existence to this arbitrary syntactic definition. If it were so, then it would be impossible to even speak of things existing without reference to their accidents. Subjects would be dependent on accidents. Whatever one may think of such an ontology, it is not the only logically conceivable ontology.
In Frege’s system, an argument a satisfies a predicate function φ(x) if φ(a) is true. Satisfying
is understood in the sense of satisfying an equation, though it is not clear how an object satisfies
a function that is not equated to anything. How are we to test for satisfaction? For example, consider φ = is round
and a = a square.
We could say φ(a) is false, but this alone does not tell us if a is not round because of logical impossibility or because of circumstances. I could say φ(b) is false where b is my balloon,
not because it is impossible for my balloon to be round, but it does not happen to be so. The balloon can still exist even if it does not satisfy this predicate relation. Frege, however, defines existence strictly in terms of the truth of a predicate statement. If φ(x) is sometimes true, then ∃x for which φ(x) is true; otherwise put: arguments that satisfy ‘φ(x)’ exist.
Russell actually believed that this stunted and arbitrary formal notion of existence is the most fundamental notion of existence. All other notions of existence are either derived from this or confused. It is hard to know whether to be impressed more by his arrogance or his naivety. We can certainly admire his willingness to pursue his assumption to its absurd conclusions. Russell infers that it is incorrect to ascribe existence to an individual. Rather, Men exist
↔ ‘x is a man’ is sometimes true,
and nothing more. Since existence pertains only to the indeterminate men,
we cannot infer the same about an individual (e.g., Socrates). Just as we cannot infer:
Socrates is a man.
Men are numerous.
∴ Socrates is numerous.
Neither can we deduce:
Socrates is a man.
Men exist.
∴ Socrates exists.
Socrates
is not an argument, according to Russell, so it is meaningless to say he exists. In other words, for Russell, as for Frege, existence pertains to the x in φ(x), but not to any determinate constant a making φ(a) true. Modern logicians find it problematic to infer from the universal to the particular, since they fail to grasp the ontological similarity of ‘is’ in ‘X is P,’ whether X is universal or particular. Some even deny that ‘Every X is P’ implies that ‘Some X is P,’ but insist we need an additional existential premise (∃ some X). This distinction is unnecessary if we apply the aspect theory of interpreting predication. The most elementary inferences become problematic to modern logicians because they have become slaves to their formalism, and if a common-sense inference such as (Every X is P → Some X is P) cannot be justified by their formalism, they will say common sense is confused
rather than admit deficiency in their formalism.
According to Russell, we can affirm existence only of descriptions. Simple ontological assertions, like ‘a exists,’ are mere noises or sounds, meaning nothing. Begging Russell’s pardon, it means a great deal whether we say ‘a exists’ or ‘a does not exist.’ What Russell really means is ‘a exists’ has no reference, according to his theory of description. That is well and good, but there is more to valid intellectual activity than his theory can embrace. He abuses his function as a builder of a logical system by dismissing metaphysical questions before they can even be asked. He builds his narrow metaphysical notions into his logic, yet logic should be able to handle all conceivable metaphysics. Russell’s cannot even handle ‘a exists’! Following Hume’s bad example of declaring perfectly cogent statements meaningless because they do not fit into his theory, Russell also follows him in the denial of the existence of real, metaphysically valid terms.
Other analytic philosophers, more soberly, have not always accepted Russell’s notion of existence. Our ability to distinguish the real from the non-real or imaginary enables us to investigate fictions, universals, abstractions and other logically cogent entities. We need a logic with no assumptions about existence. If we decide a priori what exists and what does not exist, that is absurd, not to mention utterly contrary to the empiricist program Russell hoped to advance. Instead of pretending that ‘a exists’ is unintelligible, he should have admitted that this theory of descriptions does not encompass all of logic.
The observant reader may have noticed that at the base of Russell and Frege’s account of existence is a set theoretic understanding of reality. Set theory, as we shall see later, conflates the conceivable with the actual (as no such distinction is necessary in mathematics) and universals with objects. It is unsurprising, then, that their logic similarly lacks such distinctions, and gives such an impoverished account of existence. This is what comes of letting our formalism do our thinking for us, rather than allow our thinking to pass judgment on the formalism.
In classical logic, all deductive logical inferences are expressed as syllogisms. In a syllogism, the major and minor premises share a common term, while the conclusion shares a term with each of the premises. The structure may be modeled as follows:
Major premise: M—P
Minor premise: S—M
Conclusion: S—P
We do not specify above the relationship between terms (represented generally by a dash), as the nature of the relationship indicates the type of syllogism. Perhaps the most basic type is the categorical syllogism, where the relationship between terms is a predicate attribution, either of a universal to a subgenus or particular, or of an accident to a subject. In order for such syllogisms to be valid, we must assume some sort of transitivity of attribution, enabling us to infer:
M is (a) P
S is (an) M
S is (a) P
Consider the case where S is a particular object, while M and P are universal substances. For example,
Man is an animal.
Callias is a man.
Callias is an animal.
In the major premise, the predicate relation is that of subordination, while in the minor premise it is that of instantiation. Nonetheless, we can make a valid inference from these premises since both subordination and instantiation attribute the essence of the predicate to the subject. Man is an animal
means that the essence of animal is fully attributable to man, so that the essence of animal is the essence of man, so that which is a man is also an animal. Callias, by instantiating the essence of man, also instantiates the essence of animal. Thus we have:
M is a subgenus of P.
S instantiates M.
S instantiates P.
Another type of categorical syllogism is where S is a particular object, M is a universal substance, and P is a property.
Birds have wings.
My pet is a bird.
My pet has wings.
M is characterized by P.
S instantiates M.
S exemplifies P.
The major premise is not All birds have wings,
but a stronger statement, namely that it is essential to being a bird to have wings. Since my pet is an instance of bird,
it has the essence of bird
which includes the differentia has wings.
The inference is valid for the same reason as previously: whatever has the essence of a universal has the genus and differentia of the universal.
Note that we do not assume that there is a real thing that is the essence of the universal substance. We only need to consider entities conceptually, so these syllogisms are truly rules of thought or logic, and not theses of metaphysics.
Categorical syllogisms can also have the quantifiers all,
some,
or none.
For example:
All M are P.
Some S are M.
Some S are P.
This inference holds when S is subordinate to or an instantiation of M, whether P is a universal substance or property. S exemplifies, instantiates, or is characterized by P according to the categories of S and P.
In addition to categorical syllogisms, Aristotle also defined modal syllogisms, where premises are modified by, It is necessary that…,
It is possible that…,
or, It is impossible that….
For example:
It is possible that M is P.
It is possible that S is M.
It is possible that S is P.
This holds wherever the categories of the terms admit a valid syllogism. Some early analytic philosophers denied the validity of modal syllogisms, but modal logic has been developed into a modern formalization, and has formed a fruitful part of modern philosophy. However, as we have commented in Logic and Language, modern logicians often conflate necessary
with probability 1, and impossible
with probability zero, though measure theory should make clear that these are distinct concepts. The chance of picking a rational number from the real numbers at random is probability zero, but not logically impossible. Similarly, the chance of picking an irrational or transcendental number is probability 1, but it is not logically necessary that a real number should be non-rational.
We may identify the types of categorical syllogisms according to the fundamental category of each term. By fundamental category, I mean the four classes of the ontological square: universal substance, universal accident, particular substance, particular accident. This is not to be confused with Aristotle’s ten categories (substance and nine categories of accident), which are the highest predications of being. For succinctness, I will use the terms object, kind, property and trope as shorthand for particular substance, universal substance, universal accident, and individual accident, respectively. By this nomenclature, I do not intend to define these concepts any differently than from what was discussed in the Introduction to Ontological Categories. Using this system, we have the following possibilities of categorical syllogism:
| S | M | P |
|---|---|---|
| object ” ” ” | object kind property trope | (1) object, (2) kind, (3) property or (4) trope (5) kind or (6) property (7) property (8) property or (9) trope |
| kind ” | kind property | (10) kind or (11) property (12) property |
| trope ” | property trope | (14) property (15) property or (16) trope |
It would seem that there are sixteen possible types of simple categorical syllogism, but there is a further refinement we can make, since kinds can be predicated of kinds and properties of properties either by identity or subordination. We will make the ontological predicates explicit as we give examples of each type of syllogism.
Syllogism 1: S, M and P are objects
M is P.
S is M.
S is P.
Mr. Jones is my landlord. (identity)
Bob is Mr. Jones. (identity)
Bob is my landlord. (identity)
By identity,
we mean that both terms refer to the same particular object. Since the same relation holds in both terms, and the transitivity of identity seems self-evident, this should be the most obviously valid syllogism. (We assume, naturally, that terms are used unequivocally, so the Mr. Jones
of the major premise has the same referent as Mr. Jones
in the second premise.) Nonetheless, this is a real constructive inference, not obvious to everyone. If we give the abstract form:
M is P.
S is M.
S is P?
…some people would say, innocently enough, No, S is not P, because you just said S is M!
While we may smile at such naivety, it should give us pause about declaring the transitivity of identity to be self-evident, in the sense of involving no rational construction. It is conceivable that people would take M is P
and S is M
as two independent statements, without recognizing one as having any bearing on the other. Our recognition that they can be combined to construct something new is perhaps the most primitive form of inference (though modus ponens may also make that claim). Transitivity of identity can be understood if we accept reflexivity, namely S is M → M is S.
The reason for this is that ‘is’ simply means that both S and M refer to the same object—call it X. So:
S is M → (S refers to X) and (M refers to X)
Since M is used univocally, it must have the same referent in the major premise (M is P
), so again M refers to X. The identity M is P
can only be complete if M refers to X and P refers to X. Now, we can take pieces of each premise—S refers to X and P refers to X—and construct the identity S is P.
Symbolically, we could write:
M(X) ∧ P(X)
S(X) ∧ M(X)
S(X) ∧ P(X)
What if P was not an object, however? Then we could not make the major premise an identity. Since S is identical with M, anything predicated of M is predicated of S in the exact same way. Thus if P is a kind (Syllogism 2), then both S and M instantiate P. (M instantiates P and S instantiates M
implies S instantiates P.
) Identity means that two terms are different labels for the same thing, so the terms can be used interchangeably without any change in reference or meaning. Similarly, in Syllogism 3, both S and M exemplify P, and in Syllogism 4, they substantiate P.
When M is not an object, we no longer have identity even in the minor premise, so we must find another basis for validity. Take the case where M is a kind and P is a kind (Syllogism 5). If M is P
were intended as an identity (i.e., these are different terms for the same genus), we could validly infer that S instantiates P given that it instantiates M. Let us suppose, however, that M is P
signifies not identity, but subordination, as in Man is an animal.
This statement means that the essence of animal is essential to man; that is, being an animal is indispensable to being a man. The concepts man
and animal
are so defined that it is inconceivable to be a man without being an animal. An object that instantiates a universal manifests the essence of that universal. If Socrates instantiates man,
that means whatever is essential to man pertains to the constitution of Socrates. Now, instead of referents, we must speak of essences, which is why modern logic fails to grasp the simple syllogism: Socrates is man; man is animal; therefore Socrates is animal.
Languages such as Greek or Latin that do not use an indefinite article make the universality of terms more obvious. Yet even in English, Man is an animal,
does not necessarily indicate a set theoretic notion of man
being an object in a set of animals, but rather that the notion of being an animal is contained in the notion of being man. Thus whatever is essential to an animal (i.e., necessary to render an object identifiable as an animal) is also essential to man. The essence of animal is contained in the essence of man, so that whatever has the essence of man has the essence of animal in the exact same way. Since an individual such as Socrates has the essence of man by means of instantiation, he also has the essence of animal by the same means, that of instantiation. Note we assume that (a) instantiation is a means by which something can have an essence, and (b) the essence of animal belongs to that of man in a way that does not in any way distort or impair the essence of animal.
This talk of essences may seem to introduce metaphysics into our logic; on the contrary, the notion of an essence is less tied to a posteriori reality than referents. An essence need only be conceptual, while a referent (in Russell’s sense) is supposed to exist. We consider both essences and referents a priori, without assuming their reality or actual existence. An essence is that which makes a thing what it is; for a universal entity, the essence and the entity are one and the same, since a universal term signifies nothing other than a kind of thing. An object, by contrast, may have accidental attributes in addition to being an instance of some universal. Its essence,
if we may define one, would include not only the essence of its universal, but also its accidental qualities and its thisness,
not shared by the universal. The reason we call the essence what it means to be a thing is that essence is an entity abstracted from its existential state. We do not need to know whether a unicorn exists to know what a unicorn is. The ‘is’ here refers to conceptual being, and the essence is nothing other than the constitution of an entity’s conceptual being. We are more firmly in the realm of logic than is modern logic, since we are dealing with pure thought, not objects.
When S is an object, M is a kind, and P is a property (Syllogism 6), our syllogism takes the form:
M is characterized by P.
S instantiates M.
S exemplifies P.
This syllogism is trivially valid if we suppose S exemplifies P
to mean nothing more than the conjunction of the first two premises. Yet we can often know that an object exemplifies a property without direct reference to some universal substance, so S exemplifies P
should mean something more, making this a less obvious syllogism. S exemplifies P
means that the essence of P is manifested in S. Since S is an object, it cannot be an instantiation of P, though an instantiation of P may be said to inhere in S. Indeed, since a trope is nothing more than an instance of its universal, S exemplifies P
is logically equivalent to, An instance of P inheres in S.
The statements are not identical, since S exemplifies P
means only that the essence of P can be found in S, without explicitly saying that P must be instantiated in order to inhere in S. Does this mean tropes are logically necessary to property-object logic? Only as a concept, but we do not need to consider the trope as a distinct entity. What is necessary is that the essence of the property be instantiated when it is manifested in a particular object.
Given that S exemplifies P
is equivalent to An instance of P inheres in S,
can we justify Syllogism 6? M is characterized by P
means the essence of P, which is P, is a constituent of M. This relationship is distinct from subordination, since the essence of P is not simply a less specific substituend for M. For example, if Man is an animal,
then animal may be used in substitution for man,
with the understanding that we are being less specific. However, rational
could not be substituted for man, since there are many aspects of man
not contained in rational.
The entire essence of man,
however, falls under the essence of animal,
related as the specific to the generic. A man is a kind of animal, but it is not a kind of rational
or rationality. We may say that man is one of many rational entities, but these more generic entities must be of the same category as man, which is substance. The essence of the differentia modifies the genus animal
so that a specific type of animal, man,
is indicated, yet this man is fully animal, retaining the entire essence of animal. Rational pertains to man as being in a subject. Man is rational
means nothing different than Socrates is rational,
save that in the latter case the subject is on the order of particular. Expressed schematically, we have:
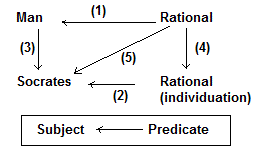
In both (1) and (2), the relationship between subject and predicate is the same, just as the relationship of instantiation is the same in both (3) and (4). Since we have already shown that (5) is equivalent (2) and (4) combined, it follows that it is also equivalent to (1) and (3) combined. (1) and (3) are the premises of Syllogism 6, while (5) is the conclusion, so the syllogism is valid.
In Syllogism 7, S is an object, M is a property, and P is a property. If the relationship between M and P is identity (i.e., they are different names for the same concept), the syllogism holds trivially. Let us suppose, then, that M is subordinate to P. A subordinate property has the essence of more generic properties as an essential constituent, so it is not possible to possess the subordinate property without possessing the generic property in the same way. Since S possesses the essence of M by way of exemplification, S must also possess P by exemplification.
If S is an object and M is a trope, P may be a property (Syllogism 8) or a trope (Syllogism 9). The minor premise is that M inheres in S. M is in S as being contained by S, not as a part, and is dependent on S. If P is a property, we may make the major premise that M is an instance of P, in which case S exemplifies P, since this is logically equivalent to, An instance of P inheres in S.
If P is a trope, the syllogism holds trivially, since the only categorical relationship we admit between tropes is identity. (Other relationships are possible, but they do not involve an attribution of essence between tropes.)
Suppose both S and M are kinds. Then P can be a kind (Syllogism 10) or a property (Syllogism 11). Naturally, if any of these relations are identities, the syllogism holds trivially. Let us suppose, then, that the relationships between kinds are of subordination. If S is subordinate to M, and M is subordinate to P, then S is subordinate to P, since the essence of P is fully attributable to M as such, and S receives it entirely as it receives the essence of M. If S is subordinate to M and M is characterized by the property P, then S will also be characterized by P. This is less obvious than the previous result. Suppose the M is subordinate to some genus Q, where P differentiates it from other kinds of Q. This supposition is justified by the fact that M has a property P, so we could generalize to entities that do not necessarily have that property. The essence of M is Q—P,
where Q and P are genus and differentia. The essence of S, being subordinate to M, receives the essence of M in its entirety. This is nothing other than Q—P,
so S shares the genus and differentia of M. Q is a genus of S no less than M is, and since S is subordinate to M, it must at least possess the differentia P, in addition to the other differentia(e). Thus S is characterized by P, though P necessarily is not the sole differentia of S.
If S is a kind and M is a property, P can only be a property. (Syllogism 12) Again, if M and P are identical, the syllogism is trivial, so let us suppose they are related by subordination. If M is subordinate to P, the entire essence of P pertains to M, with P being a more generic property. Naturally, if S is characterized by the more specific property M, it must also be characterized by the more generic property P.
If S and M are both properties, P must also be a property. If there are no identities, and they are related by subordination, the syllogism obviously holds. If S is subordinate to M and M is subordinate to P, then S must be subordinate to P. (Syllogism 13) Suppose S is a trope. Then M can only be a property or a trope. If M is a property, P must also be a property. If S instantiates M, it must also instantiate P. This is because the entire essence of P is contained in the essence of M, of which S is an instance. (Syllogism 14) If S and M are both tropes, the syllogism holds trivially, regardless of whether P is a property or trope (Syllogisms 15, 16), since tropes (S and M) are related to each other only by identity.
Categorical syllogisms can be modified by the quantifiers all,
some,
or no.
If we understand these quantifiers to span the range of all conceivable instantiations of a universal, then all X
serves as an effective surrogate for a universal. When we say, All men are rational,
we mean all conceivable individuals who are men are also rational. This is logically equivalent to, Man is rational.
It would be a mistake, however, to equate all men
with the universal man
in all sentences. For example, Socrates is man
(meaning Socrates instantiates man) is not the same as, Socrates is all men.
All men
asks us to consider the instantiations of man in toto, while man
is abstracted from individuation. We should proceed carefully, then, in seeing how quantified syllogisms may be made valid.
The quantifiers may only be applied to individuations of substance (they may also be applied to tropes, but these yield only banalities, such as, All instances of white are white
), and we are not concerned with trivial identities, so we need only consider Syllogisms 1-9, it would seem. However, quantificational syllogisms are not simple categorical syllogisms, as can be seen by this example.
All men are animals.
All Greeks are men.
All Greeks are animals.
This differs from a simple categorical syllogism since the middle term is not identical in the two premises. Men
≠ All men.
The syllogism is valid, as we can tell from one constructed of logically equivalent statements.
(Syllogism 10)
Greek is subordinate to man. Man is subordinate to animal. Greek is subordinate to animal.
Might we nonetheless justify the quantificational syllogism without appeal to the analogous categorical syllogism? Let us parse the meaning of each premise.
All X is Y
…means every (conceivable) instance of the universal X instantiates (exemplifies) the universal substance (accident) Y. This means that for any (conceived) object x, we may say If x instantiates X, then x instantiates (exemplifies) Y.
Applying this to our example:
If x instantiates Greek, then x instantiates man.
If y instantiates man, then y instantiates animal.
If x instantiates Greek, then x instantiates animal.
This syllogism holds, when we consider that any x in the first premise may be substituted for y in the second premise. We need only show that the conclusion is logically equivalent to the conclusion of the quantificational syllogism, All Greeks are animals.
We have already shown the forward implication; it remains to show the reverse: If x instantiates Greek, then x instantiates animal
→ All Greeks are animals.
Suppose the negation of All Greeks are animals,
namely, that there is at least one Greek who is not an animal. This object, x0, instantiates Greek (i.e., x0 is Greek), yet if x0 instantiates Greek, then x0 must instantiate animal. So it is impossible for All Greeks are animals
to be false if the first statement is true, so the implication holds.
The quantifier some
can also be used in syllogisms. For example:
Some X is Y.
All Y is Z.
Some X is Z.
Some X is Y
means that for some (at least one, and as many as all) instances xi of X, xi instantiates (exemplifies) Y. The second premise (suppose Y is substantive) says that if y instantiates Y, then y instantiates (exemplifies) Z. We could express this modally:
If x instantiates X, it is possible that x instantiates Y.
If y instantiates Y, then (it is necessary that) y instantiates Z.
Given the first premise, we may postulate some potential object x0 that instantiates both X and Y. Then we let y = x0, from which it follows that x0 instantiates Z. Thus there is some x, namely x0, that instantiates both X and Z. We know not only that some X is Z, but we know which X, namely those x which are Y (though there could be others as well).
This modal approach could be equivalently represented in a set theoretic way, where we consider a set of all conceivable instantiations of a substance. All X
means every member of X = {xi}, where xi instantiate the universal X. Note that X, the set of all instantiations, is not the same as X the universal. (Modern set theory fails to make such a distinction.) Some X
simply means some non-empty subset of X. This definition, which exactly matches what we ordinarily intend by all
and some,
makes it obvious that All X is Y
implies, Some X is Y.
In modern logic, the second statement requires an additional existential axiom: There exists an x s.t. x is Y.
We avoid this necessity, since we consider existence only potentially (conceivably). Alternatively, we could use the aspect theory to interpret All X is Y,
so that existence is built into the statement. Since we stick to a priori logic, we are not left with the bizarre finding that Some X is Y
cannot be inferred from All X is Y.
Using our corrected set theoretic model, we analyze the syllogism as follows:
Some X is Y.
All Y is Z.
Some X is Z.
B ⊆ Y, where B ⊆ X and B ≠ ∅
Y ⊆ Z
B ⊆ Z, where B ⊆ X and B ≠ ∅
Note that ‘Some X is Y’ can also be interpreted as X ∩ Y ≠ ∅, though this does not grasp the subordination of X to Y. The use of subsets does not fully grasp this subordination either, though at least we have an asymmetric relation. If we made Z a property rather than a universal substance, then Z would be the set of all objects that exemplify Z.
Lastly, we can use the negative quantifier ‘no’ in a syllogism. For example:
All X is Y.
No Y is Z.
No X is Z.
No
is the complement of some.
In modal language, it means, it is impossible that;
in existential language, it means, there does not exist an x such that…,
but in our common sense modified set theoretic formalism, it can be expressed as follows:
X ⊆ Y
Y ⊆ Zc (or Y ∩ Z ≠ ∅)
X ⊆ Zc
The introduction of the complement set Zc is justified by the equivalence of the statements No X is Z,
and All X is not Z.
These are equivalent only if we suppose is not Z
to deny that Z is predicated of the subject, but not necessarily implying that some other thing is predicated in its place. Yet a complement set would be an unsuitable model for this scenario, where the subject has no predicate whatsoever. It would be better to state it simply as a negation of Some X is Z,
i.e., ¬(B ⊆ Z) where B ⊆ X and B ≠ ∅. This negation must hold for all B ⊆ X, except where B ≠ ∅. This includes any set containing x ∈ X, whence it follows that for all xi ∈ X, {xi} ⊈ Z. We will not worry too much about the distinction between elementhood and sethood right now, so we can just use sets of one element. We are only using set theoretic formalism as a surrogate for what we actually intend by quantified statements. Actual set theory only imperfectly represents what we intend, rendering inferences such as All X is Y
→ Some X is Y
impossible. The deficiency is not in the inference, but in the formalism. It is imperative that we are the masters of our logical formalism, which is but a tool, and we do not let the formalism dictate to us what is inconceivable or illogical if we have already conceived it and explained it cogently.
We have already alluded to the possible similarity between quantified syllogisms and modal syllogisms. We will now deal with modal syllogisms in their proper sense. The statement, It is possible that X is Y,
might be interpreted to mean Some X is Y.
Yet we can use modal logic even when the subject is a determinate individual: It is possible that x0 is Y,
where x0 is a determinate object and Y is a universal substance or accident. Here possibility is considered in terms of the various possible scenarios or circumstances in which x0 might exist, or may be considered subjectively from the perspective of an ignorant observer or thinker. When we intend logically possible,
we mean that the dictum (x0 is Y
) is neither logically necessary nor logically impossible. That is the classical definition of possible,
at any rate. However, in modern usage, it is common to use ‘possible’ in a sense that includes necessary.
To avoid this ambiguity, I will use ‘possible’ in the modern sense, and ‘contingent’ in the classical sense, excluding necessary.
Thus we define these statements:
It is necessary that x0 is Y. (In all logically conceivable scenarios where x0 exists, x0 is Y.)
It is contingent that x0 is Y. (In some, not all, logically… )
It is possible that x0 is Y. (In some or all logically… )
It is impossible that x0 is Y. (In no logically… )
Modality can be expressed as quantifiers on logically conceivable scenarios. We should stress that ‘all’ really means all, and not just probability 1. As mathematicians know, it is possible for an event to have probability 1, yet not encompass all possible events. For example, the probability of picking a non-natural number out of the real numbers is 1, yet clearly it is not logically necessary for a real number to be non-natural.
Modal logic differs from standard modern logic in that it explicitly allows for ambivalence regarding the existence of its objects, so we are unabashedly considering things a priori, abstracting from whether or not they actually exist. Russell’s ontological straitjacket would not fit on modal logic, so he rejected it, but later logicians have come to recognize a useful formalism for it can be developed, with fruitful results, especially in areas like quantum mechanics where we are forced to admit ambiguity in existential states, distinguishing the potential from the actual.
Logical possibility means that there is a logically conceivable condition whereby the dictum would be made true. Generally, we can judge a thing to be possible by actually conceiving of one such condition, or else by formally showing that the existence of such a condition cannot be excluded a priori, even if we are unable to conceive of it directly. To prove that something is impossible, we should show that it involves a logical contradiction, since it would be generally impossible to exhaustively explore every possible scenario. To show that something is necessary, we may deduce it from some tautology, or show that its negation would lead to contradiction.
Since we are doing logic, not metaphysics, we do not need to judge whether the statements in question are actually true. We only need to consider, on the supposition that some premises are true, would the conclusion be true? When the premise is modal, the truth of the dictum (though not of the premise as a whole) is ambiguous. In late Scholastic philosophy (c. 16th cent.), it was common to interpret the possible and actual as mutually exclusive, so one could hold actually false propositions to be at least possible.
This sounds strange to modern ears, for we do not regard the actual as excluding the possible, yet we do regard actual falsity as resolving the probability as zero. In this latter case, we are considering a posteriori possibility, but the late Scholastics always considered possibility a priori. For unrealized anterior possibilities, we may use subjective conditional statements, e.g., It would have been possible for him to succeed if he had applied himself,
with the latter clause indicating that the requisite condition was not realized. Neither of these models is invalid, but we need to be clear whether we are considering anterior or posterior probability. In simple modal statements such as we have discussed, probability is always considered a priori. We say nothing about whether the statements are actually true or false, so we are not in a situation where we have to declare an actually false statement possible.
Obviously, each statement carries the implicit declaration that it is true, but we can test the relation of the potential truth values of statements using rules of inference.
Transitivity of attribution holds when we are dealing with relations of subordination: If S is an M and M is a P, then S is a P.
This is nothing other than categorical Syllogism #10, discussed previously. With quantified negative subordination, we have a reversible commutative relationship. If no S is an M, then no M is an S.
Since we are using quantifiers, we are referring to individuals, in the way described earlier.
No S is an M↔ ¬(B1 ⊆ M), if B1 ⊆ S and B1 ≠ ∅
→ ¬(s ∈ M), where s ∈ S
No M is an S↔ ¬(B2 ⊆ S), if B2 ⊆ M and B2 ≠ ∅
→ ¬(m ∈ S), where m ∈ M
We can see the first statement implies the second, by supposing the contradiction of the second, namely that some M is an S. Then there is some B0 ⊆ M where B0 ⊆ S and B0 ≠ ∅, and so there is an s ∈ M where s ∅ S. Thus the intersection of S and M is non-empty, which means there is some S that is an M. This contradicts the first statement, so the inference holds. This reciprocity holds only because we are able to model instantiation in this set theoretic way; for other categorical relations there can be no reciprocity. For example, the reciprocal of No S exemplifies M
(where S is a substance and M is a property) would be No M exemplifies S,
which is categorically unintelligible.
We can also construct syllogisms using superordination, which we represent with set theoretic shorthand: S ⊇ P.
S ⊇ P
No M belongs to S.
No M belongs to P.
Animal ⊇ Man
No M belongs toanimal
No M belongs toman
[No A belongs to B
means: ∀a ∈ A, a ∉ B. In other words, no instance of A instantiates B, or is any instance of A identical with any instance of B.]
Suppose, contrary to the conclusion, that some M belongs to P. Then it must also belong to S, by the first premise. Yet this is contradicted by the second premise.
Beyond Aristotle’s categorical and modal syllogisms, which seem to encompass almost any rule of inference, Boethius introduced the hypothetical syllogism. Aristotle’s syllogisms used universal terms only, but we can see how this could be expanded to individual terms. Boethius’ hypothetical syllogism makes best sense when dealing with universals, since these are considered abstracted from the question of existence, though we may do the same with individuals. Since modern logic dismisses universals out of hand, it cannot deal with hypothetical syllogisms properly. The closest analog to the hypothetical syllogism is sentential logic, to be discussed in greater detail.
Seeing that the syllogism may express relations among universal terms, the question arises as to whether these relations pertain to the extension of the terms or their comprehension. ‘Extension’ means the range of applicability of a term, i.e., all the potential subjects to which it may be applied. ‘Comprehension’ means the term’s conceptual content, i.e., the characteristics that define it. Boole and most modern logicians have tended to emphasize relations of extension. Jacques Maritain, on the contrary, held that it is equally legitimate to consider the syllogism as relating terms in the order of comprehension. Aristotle exhibited both tendencies in his interpretations.
A further interpretive nuance lies in how we construe the syllogistic inference. We might express this simply as: P. Q. Therefore C,
where P and Q are the premises, and C is the conclusion. Aristotle, however, saw the syllogism as a compound expression, of the form: If P and Q, then C.
In other words, it is a compound hypothetical proposition, not a series of simple categorical propositions. The views of Aristotle and Maritain are compatible with the modern conventional depiction of the syllogism, but we should examine how they may enhance an inferential claim.
In the standard, minimalist interpretation, we may say, Assume P is true. Assume Q is true. Then C must be true.
We can only deduce that C is true, however, if we conceive of a shared reality where both P is true and Q is true. Thus we must hold with Aristotle that we need a compound expression: P ∧ Q. The `∧’ (and
) represents a coupling of the two assertions as applying to the same reality. This is a logical connective, which expresses a logical relationship between propositions, creating compound propositions. It would seem, in this interpretation, that the intuition behind the connective ∧ is already implicit in the structure of a syllogism. Further, we must understand what is meant by ‘If P ∧ Q, then C,’ in terms of connecting the compound premise to the conclusion. If we consider the terms in the order of their extension, we shall find that the conclusion is true to the extent that the premise is true. We can see this with the following example.
All A’s are B’s.
Some B’s are C’s.
Some A’s are C’s.
The quantifier some
is specified to the same extent in the conclusion as in the second premise. There ought to be rules to express systematically the relationship between the extension of terms in the premise and those of the conclusion. Such rules actually have been formalized; they are the eight classical rules for forming a syllogism.
The eight Scholastic rules for forming syllogisms are summarized as follows:
These are not arbitrary rules imposed on syllogisms; rather they are shorthand reminders about the possible forms of syllogisms, which can be deduced from the logical structure of a syllogism. They all refer to terms, their extension, and the affirmation or negation of a premise. We will consider these rules as applied to categorical syllogisms, though the reader may see how they apply to other modalities.
We return to our basic syllogistic structure:
Major premise: M—P
Minor premise: S—M
Conclusion: S—P
P is the major/first term, S is the minor/last term, and M is the middle term. Clearly we have at least two terms in an inference, for a logical assertion must have at least two of them, as discussed in our Introduction to Ontological Categories. We may call these terms S and P. If the premises consisted of nothing but S and P, at least one of the premises would have to be S—P in order to obtain the conclusion. This is nothing but simple identity, and not a constructive inference at all. Indeed, the other premises are rendered superfluous. In order to have a non-trivial inference, then, it is clearly necessary to have at least three terms. Obviously, we could have four or more terms in a complex argument with multiple inferences, but we are concerned with building arguments from the smallest possible units. Since a two-term argument yields nothing but the same proposition, it cannot be part of a bigger argument. A three-term syllogism, as we shall see (and have seen), yields a conclusion different from either premise, so it can form a part of much more complex arguments (though it is beyond our present scope to show that all arguments can be expressed as a series of syllogisms).
The second rule, that no term may have a greater extension in the conclusion than in the premises, only applies to terms S and P, since only they appear in the conclusion. If the premises were to contain only a limited extension of S (e.g., some S
), we would not be able to say anything about all S.
We cannot prove anything about an extension of S that is not even discussed in the premises.
The third rule, that the conclusion may not contain the middle term, seems strange. If we cannot give a proper account of this, we would have to show how the second rule applies to M. The middle term, by definition, is that which appears in both premises. We could have:
| (1) | (2) | (3) | (4) |
|---|---|---|---|
| M—P | M—S | S—M | M—S |
| S—M | P—M | P—M | M—P |
Numbering these pairs of premises 1 to 4 from left to right, (1) gives our standard (first figure
) syllogism; (2) is logically equivalent in form (we have just swapped S and P); (3) gives a syllogism of the second figure,
only if one of the premises involves a negative, and (4) gives a syllogism of the third figure. (Second and third figure syllogisms will be discussed more fully later.)
Can the conclusion of the first figure (1) contain the middle term? Apart from trivial repetitions of the premises, the only possible conclusions with M are P—M, M—S, or their negations. Yet these can be conclusions only if the terms’ copulative relationship is reflexive (M—P → P—M), i.e., identity. The conclusion would follow from only one of the premises, rendering the other superfluous. Can a conclusion involving the middle term be deduced from a true synthesis of premises, preserving an asymmetric relationship (as the subject-predicate relationship is generally)? In other words, can the conclusion P—M or M—S (or negations) be derived from a conventional syllogism? It is possible for M—P and S—M to be true, in general, regardless of whether P—M or M—S are true or false (save when the copula is reflexive). The coupling of M—P and S—M works in the middle term, namely to connect S to P. Any constructive conclusion, therefore, will involve S and P. The prohibition against including M in the conclusion is not grounded in logical necessity, but to exclude non-constructive conclusions from consideration.
Similar reasoning applies to the second and third figures. The only possible conclusions involving M would be the converse of one of the premises, which could hold only if the ontological relationship between subject and predicate is identity. Again, no constructive conclusion that is substantially different from either premise is possible if the middle term is one of the terms of the conclusion.
The fourth rule holds that a middle term should be taken at least once in a general form (generaliter). If, on the contrary, we take it to be a particular, determinate entity in both instances, we get the following: (This M)—P; S—(This M). In order for both premises to be intelligible, the copula must be able to accept a particular in both terms. To take an example: Flipper is a mammal;
Dolphin superordinates Flipper.
Yet we cannot say anything definite about the relationship between mammal and dolphin, save that they both relate to Flipper, which is already explicit in the individual premises. This is because the presence of a particular term in each premise restricts the applied extension of each general term dolphin,
mammal,
so we cannot relate general to general. The only way we can draw a conclusion is if either the major or minor premise is an identity (e.g. Flipper is this dolphin), in which case we get a trivial re-labeling conclusion. Again, the only way to get a logically constructive conclusion is to respect this constraint.
That nothing follows from two negative premises seems to have been lost on Bertrand Russell, judging from his definition of material implication. Unlike this pseudo-implication, we are not concerned with material conditional statements, but with logical inferences. It must be understood that negation here applies to the copula (e.g., x is not P,
rather than x is not-P
) In our standard syllogistic form, we suppose M is not P and S is not M. We cannot use the middle term to bridge the gap between S and P, saying two negatives make a positive, or a negative for that matter. Just because S is not M and M is not P, it does not follow that S is or is not P. We would have to introduce some other premises before we could make any inferences. Negations do not assert any definite ontological relationship between terms; thus we cannot use them to yield positive knowledge of an ontological relationship, other than to deny those they deny.
If both premises are affirmative, the conclusion cannot be negative. When we assert M is P
and S is M,
we affirm two ontological relationships. It may seem strange that we cannot yield negative knowledge from positive knowledge, which is more perfect, given that the conclusion ought to be the weakest statement. To prove a statement of the form S is not P,
we would need some negative premise or an affirmative premise that excludes S is P.
For suppose S is Q
proves S is not P,
meaning S is Q
is exclusive of S being P. In order to know this, we must know a priori that being Q entails not being P. This entails knowing that Q is not P, for if we were not certain Q is not P, how could we know that S is Q
does not mean S is P
? Further, we must know that Q does not superordinate P, or else S is Q
would imply S is P.
So, in any scenario, we need some negative premise in order to yield a negative conclusion.
The conclusion is always the weakest point, or more exactly, it cannot be stronger than either of the premises. This follows indirectly from the second rule, that no term can have greater extension in the conclusion than in the premises. Yet it is more expansive than the second rule, and constitutes a distinct (sixth) rule, as can be seen from the following model. Let x1, x2, x3… be the quantifiers of a term, and define xi > xj if xi is more universal than xj. Then a syllogism may have the form:
x1A is x2B
x3B is x4C
x5A is x6C
By the second rule, x5 ≤ x1 and x6 ≤ x4. Nonetheless, we could conceive of a case where this rule holds, yet the conclusion is stronger than one of the premises. This is by considering modality. For example:
Every A is certainly a B.
A B is possibly a C.
Every A is certainly a C.
This is an invalid syllogism, because the modality of the conclusion is stronger than that of one of the premises. If it were possible to reduce modality to quantification, then we could effectively reduce the present rule to the second rule. That might work when probabilities can be quantified, but not for degrees of certainty, such as metaphysical, moral, etc. Yet even quantifiable probabilities do not necessarily reduce modality to quantifiers, despite a numerical equivalence. For example, the statement, There is a 50% chance that all As are Bs
is logically distinct from 50% of all As are Bs,
even though the numerical probability of an A being a B is the same in both cases. Thus we truly do need a new rule specifying that modality in the conclusion cannot be stronger than that of any premise.
The reason for this rule is because of the way modality is coupled in a syllogism, so that the chain is only as strong as its weakest link. This principle will prove applicable to more complex arguments consisting of chains of inferences. It is an important logical tool for identifying weaknesses in an a posteriori argument. We look for the premise that is weakest and quantify the argument accordingly. We justify this rule schematically by representing the syllogism:
A—B
B══C
A—B══C
The modality of the copula in each premise signifies the strength in the bonds between terms. The identity of the middle term in both premises justifies our concatenation of premises, at least insofar as the strength of the bonds is common. The only reason we can make conclusion about the relation between A and C is because of the logical interposition of B. This modality of the conclusion, A—C, cannot be stronger than the modality of either premise. The chain is only as strong as its weakest link, and this analogy holds only because a logical syllogism, like all inferences, is a conceptually concatenative operation.
The astute reader will note that I am not giving formal logical proofs of these rules; indeed, that would be impossible, as these are the rules of logic itself. Instead, I am expanding them in order to point the reader to the intellectual intuition necessary to see that these things are true. These rules are held by people who disagree on many other things, precisely because they are grounded in a knowledge more certain than that of logical proof. Yet, notwithstanding this certainty, it is necessary for an intellect to direct his attention to a specific intuition and comprehend it, thereby achieving that certainty. Without this proper direction of intellectual attention (not to be confused with the sensitive attention
described by modern psychology), it is possible even for a rational person to fail to assent to these rules.
The last of the classical rules of syllogisms is that nothing follows from two particular premises. The reason for this is that the middle term cannot be the same in both premises unless it is a particular in both premises. Consider the alternatives:
(I) This particular A is this particular B.
This particular B is C.
This particular A is C.
(II) This particular A is a B.
This particular B is a C.
This particular A is C.
Syllogism I, while valid, is not really logically constructive. We start with an identity between this A
and this B,
so that whatever is predicated of one is predicated of the other. This A
and this B
are not conceptually distinct entities, but are different names for the same entity. Syllogism II is invalid, for there is no logical connection between the premises. What is true of one particular B, being C,
need not be true of any or all B’s, so we cannot identify the middle terms with each other.
An interesting exception to matching the quantifiers of the middle terms can be found in an additional rule of Scholastic logic: dictum de omni, dictum de nullo. Here we have:
Every A is a B.
No B is a C.
No A is a C.
Even though the middle terms appear to be direct opposites to each other with respect to quantification, they do have universality in common. When we say No B is a C,
that is equivalent to Every B is not a C.
Thus the syllogism can be completed: Every A is not a C,
or No A is a C.
Note that this does not work if we reverse, the quantifiers of the premises, i.e.:
No A is a B. ↔ Every A is not a B.
Every B is a C. ↔ Every B is a C.
The fact that every A is not a B does not tell us anything about whether it is a C. We only know that if it were a B, it would also be a C, but we know nothing about whether that which is not a B might also be a C.
There are other kinds of syllogisms, depending on the modes of the terms and the premises. By modes of the premises, I mean that which is expressed by grammatical mood, as discussed in Logic and Language. Thus far we have considered only the indicative mood (categorical syllogisms
), but we would clearly get different rules for syllogisms with premises in the conditional mood (hypothetical syllogisms
). As for the other moods—e.g., interrogative, imperative, cohortative—we do not ordinarily construct arguments from these, effectively accepting Aristotle’s judgment that these moods are only rhetorical.
Nonetheless, we might discern non-syllogistic logical rules for the relations of such statements, insofar as they entail presuppositions about truth and falsity.
By modes of the terms, I mean not only the probabilistic modes of modal logic, but any quantification of the way in which a term is posited. Earlier we discussed the suppositio of a term, which is its referent as intended by the speaker. The same term may have different referents in different contexts. For example, ‘man’ could be used to refer to the universal species man
or to an indeterminate individual, or to the linguistic object itself, depending on how it is used in a sentence. We try to distinguish the uses syntactically (for example, by using indefinite pronouns in the second case), but where this is not done, we must know what kind of suppositio we are dealing with in each instance. We have already dealt with this issue to some extent in our discussion of universals and particulars, substance and accident.
Another qualification or property of a term affecting the validity of a syllogism is copulatio, which is defined as the suppositio of a verb or predicate, so that late medieval logicians generally abandoned any distinction. Copulatio may refer to the various moods described above, as well as the affirmative, negative, etc.
Appellatio is a term’s reference to existent individuals. This is basically Russell’s notion of a referent, yet in Scholastic logic it is but one kind of suppositio. This is why Scholastic logic has more kinds of valid syllogisms than would be allowable under modern symbolic logic, which does not permit reference to classes with no existent members. Notwithstanding the oft-repeated claim that modern logic subsumes classical logic, it actually is inferentially impoverished compared to classical logic. It subsumes classical logic only in the sense of being a more generalized syntax for expressing categorical statements.
Scholastic logic also recognized other modifications of terms, such as ampliatio and restrictio, which broadened or restricted the scope of a term. A verb in the past or future tense could make the subject (e.g., horse
) be broader in scope (e.g., include all horses that existed, or all that will exist or might exist in the future). Others include alienatio (transference), diminutio (e.g., all men
in all men are evil
—we don’t really mean every single man), and relativus (his,
her,
my
). All of these properties qualify the intended supposition in the context of the proposition, thereby effecting the naming of the proposition and therefore the validity of the inference. When developing a formal logic, we must take care to account for possible equivocations in the supposition syntactically, or else posit additional rules of inference to account for these.
In Scholastic logic, the mode or mood of a syllogism often referred to the quantifiers of the premises when dealing with general/universal terms. These could be categorized into four figures,
based on the relative positions of the middle premises:
| Four Figures | I | II | III | IV |
|---|---|---|---|---|
| Major: | M—P | S1—M | M—P1 | S—M |
| Minor: | S—M | S2—M | M—P2 | M—P | Conclusion: | S—P | S2—S1 | P2—P1 | P—S |
So far, we have only dealt with syllogisms of the first figure, so-called perfect syllogisms. Yet there are also imperfect modes
in the other three figures, with apparently valid syllogisms.
Using the notation A, E, I, O for premises of different quantification, Scholastics developed a mnemonic device to summarize the valid syllogisms of each form.
(a) All A is B; (e) No A is B; (i) Some A is B; (o) Some A is not B
With this notation, we can take the first three vowels of a personal name to signify the form of major, minor and concluding premise in that order. The valid syllogisms were summarized by Peter of Spain as:

[Syllogisms of first figure in red box; second figure in green box; third figure in blue box.]
Some of the first figure syllogisms would later be assigned to the fourth. Baroco and Bocado could only be proved by reductio ad impossibile.
Recall that the first figure is M—P; S—M; ∴ S—P. Barbara has the form below. We have already shown its validity.
All B is C.
All A is B.
∴ All A is C.
Celarent is as follows:
No B is C.
All A is B.
∴ No A is C.
No animal is soulless.
Every man is an animal.
∴ No man is soulless.
This is also obvious. Note that this, like all other syllogisms, is limited by the eight rules, as well as the constraints on universals and particulars, defined for first figure syllogisms. Only then can we make a connection via the middle terms in each premise.
Darii reads:
All B is C.
Some A is B.
∴ Some A is C.
Again, this is self-evident, from what has been discussed.
Ferio:
No B is C.
Some A is B.
∴ Some A is not C.
This depends on our ability to say No B is C
→ All B is not C.
We should like to make not
modify the copula rather than C, since it is conceivable for something to be neither C nor non-C if the predicate C is simply inapplicable. Alternatively, we can assume that C is a valid predication for B.
Baraliptum reads:
All B is C.
All A is B.
∴ Some A is C.
This is trivial, and an understatement of Barbara.
Celantes reads:
No B is C.
All A is B.
∴ No A is C.
No man is an island.
Every Greek is a man.
∴ No Greek is an island.
This is also uncontroversial, except in modern formal logic, which needlessly restricts the suppositio to the appellatio.
Dabitis is identical to Darii. It was originally proposed as a fourth figure syllogism, in which case it would have the form:
All A is B.
Some B is C.
∴ Some C is A.
This would be invalid as a categorical syllogism, so Dabitis must remain in the first figure, collapsing into Darii.
Fapesmo reads:
All B is C.
No A is B.
∴ Some A is not C.
This does not hold in general for the first figure, unless we assume a hierarchy of universals. Then the fact that no A is B might tell us something about whether A is C. Otherwise, this syllogism properly ought to be assigned under the fourth figure (S—M; M—P; ∴ P—S), as was done later by the Scholastics:
All C is B.
No B is A.
∴ Some A is not C.
All men are animals.
No animal is an angel.
∴ Some angels are not men.
This requires us to implicitly assert the existence or being of “some A” (in whatever mode of being is entailed by the affirmative copula in the conclusion). This seems to understate the case. We could actually conclude that All A is not C.
Note that the first and fourth figures simply switch the order of premises. Why, then, should we regard the fourth figure as imperfect?
Kant believed that the inferences of the second through fourth figures were not real syllogisms, since they entailed additional hidden premises. For the fourth figure, he made the following criticisms. Consider this fourth figure syllogism, for example:
No stupid man is learned.
Some learned men are pious.
∴ Some pious men are not stupid.
No C is B.
Some B is A.
∴ Some A is not C.
(This is Festino, which Peter of Spain had assigned to the second figure.)
Kant contends there is an additional premise following the second, i.e.: Some pious men are learned. (Some A is B.)
We can see the validity of the syllogism with a set theoretic diagram of the premises. “Stupid men” and “learned men” are exclusive, while learned men
and pious men
have some overlap. Kant is correct to point out an implied reciprocity (i.e., L intersects P
implies P intersects L
), and he faults this syllogism for depending on this reciprocity without declaring it.
If we put Festino under the second figure (rather than the fourth as Kant does), we have:
S1—M
S2—M
∴ S2—S1
No C is B.
Some A is B.
∴ Some A is not C.
No stupid man is learned.
Some pious men are learned. ∴ Some pious men are not stupid.
This is a perfectly valid syllogism, even by Kant’s criteria. Again, we see no reason to deny that there can be perfect syllogisms in figures other than the first.
Returning to syllogisms of the first figure (M—P; S—M; ∴ S—P), we find Frisesomorum:
Some B is C.
No A is B.
∴ Some A is not C.
This is dubious in the first figure, since it requires us to assume that some B
means only some and not all. We can get a perfectly valid syllogism if we use the fourth figure (S—M; M—P; ∴ S—P) instead.
Some C is B.
No B is A.
∴ Some C is not A.
Cesare belongs to the second figure. 
No C is B.
All A is B.
∴ No A is C.
This is made evident from the diagram, leading us to Campestres:
All C is B.
No A is B.
∴ No A is C.
This is symmetric with Cesare, using the same diagram, except A and C are exchanged.
Baroco is of particular interest.
All C is B.
Some A is not B.
∴ Some A is not C.
This can only be proven (in term logic) by reducing the contrary conclusion, All A is C,
to impossibility. Suppose All A is C.
Then all A must also be B, since all C is B, but this contradicts the second premise.
A set theoretic representation makes the validity of the syllogism more intuitive. Since the set C is a subset of B, whatever elements of A are outside B must also be outside C.
The remaining syllogisms, starting with Darapti, are of the third figure.
All B is C.
All B is A.
∴ Some A is C.
Namely, those A which are B are also C. The conclusion is actually understated.
Felapton reads:
No B is C.
All B is A.
∴ Some A is not C.
Again, we understate the case, since we know which A are not C, namely those which are B.
The same may be said of Disamis, which reads:
Some B is C.
All B is A.
∴ Some A is C.
Datisi reads:
All B is C.
Some B is A.
∴ Some A is C.
Like Festino under the fourth figure, this third figure syllogism relies on some reciprocity. We must take the second premise as implying that some A is B. This would be subject to Kant’s same criticism, and fall short of a true syllogism. Datisi would be altogether invalid under the second and fourth figures, while the first is already taken (Darii). This means Datisi should either be eliminated or regarded as an imperfect syllogism.
Next is Bocado (or Bocardo):
Some B is not C.
All B is A.
∴ Some A is not C.
This requires proof by contradiction. Suppose all A is C. Then All B is A
→ All B is C.
Yet this contradicts the major premise.
Lastly, we have Ferison.
No B is C.
Some B is A.
∴ Some A is not C.
The universal negative No B is C
is the same as All B is not C
, making this syllogism more obvious.
We have only covered syllogisms, but this was by no means the limits of the power of classical logic. Other forms of inference existed, though these alone possessed absolute certainty. Yet we can discern truths beyond the tautological, and medieval philosophy treated of these as well. Modern treatments of scholasticism focus on syllogisms precisely because these most resemble modern formal logic. Yet classical logic is much broader in scope than symbolic logic, since it deals with broader notions of reference and meaning. Some of that trickles down to syllogisms, which is why not all of the classical syllogisms discussed are valid under modern logic. This fact is at odds with the claim that modern logic has subsumed classical logic. More accurately, modern logicians ignore classical logic at their peril, often leading into false paradoxes, and needlessly impoverishing logic by rendering perfectly logical arguments invalid. If formal logic is to have use for non-mathematical objects, it ought to embrace the richness of human language. Indeed, Peirce’s encyclopedic work on symbols endeavored to give us such a starting point, but along the way, the enterprise of modern logic became infested with an impoverished ontology, grounded in the anti-metaphysical prejudices of its founders, most notably Russell. On the pretext of giving us an ontologically neutral logic, we instead received a logic that assumes a narrow existential, nominalist ontology with a highly limited notion of reference. In the next section, we will look at some of the historical developments that led to this situation.
[1] Recall my convention that text in double quotes refers to the meaning of a sentence in its use, i.e., the statement, while text in single quotes refers to the mention of a sentence.
[2] Allan T. Bäck. Aristotle’s Theory of Predication (Brill, 2000).
[3] Nicholas Capaldi. The Enlightenment Project in the Analytic Conversation (Kluwer, 1998), p.77.
[4] Ibid., p.78.
© 2012, 2018 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org
| Home | Top |