Intension and extension are distinct modes of analyzing degree. We have discussed extension when describing quantity, and intension when describing quality. A more thorough discussion is found in my essay "Intensive and Extensive Magnitudes" (2004, 2007). Both intensive and extensive magnitudes admit of more or less, so they are kinds of degree. Indeed, degree might be considered a generalization of intension and extension, considering only their common attribute of admitting "more" or "less."

Substance qua substance does not admit of degree. A universal substance may be differentiated by accidents that admit of degree, e.g., "An athlete is a man who is swift or strong," so we might say something is "more" or "less" proper to the species or genus. In our example, the swifter or stronger a man is, the "more of an athlete" he is. Yet here we are considering participation in the genus via the differentiae "swift" and "strong," rather than through the substance "man." We would more properly say that a swifter man is more athletic, considering athleticism as an accident, since it is variation in a quality that we are considering. Substantial being, by contrast, is so simple and absolute that it cannot admit of variation by "more" or "less." A substance, qua substance, either is or is not.

Opposition

The ancient Greek philosophers were fascinated by the notion of opposites or contraries. This enthusiasm has diminished considerably among modern philosophers, reflecting a disenchantment with essentialism. Young children still have a zeal for learning what is the "opposite" of a thing, but to most modern adults, such knowledge is impractical, and to the more thoughtful, based on arbitrary definitions. Yet the Greeks operated on a sound intuition when they studied opposites or contraries, recognizing that any account of the diversity and multiplicity of reality ought to use opposing entities as a starting point, since the basis of all ontological logic is the distinction between "X is" and "X is not." The intuitive concept of opposites entails two entities "facing" or "against" each other, as Greek etymology would have it, so that one opposite is present to the extent that the other is absent.

Starting from this intuition, we can discern several distinct types of opposites. The most perfect or complete type of opposition would be the total presence and absence of a thing, where one opposite is an entity and the other is a non-entity, so that they are opposed not only in all aspects of their being, but even in existence itself. This opposition, when applied to accidents of a substance, is known classically as privation and possession. Less radically, two opposites might share existence as entities, yet remain in opposition with regard to certain aspects of their being. These opposites are classically called contraries. Lastly, some opposites might be so intimately related that, though they are opposed, they are defined with respect to each other, and neither one can have existence without the other. These are known as correlatives.

Perhaps following a similar intuition, Aristotle identified four types of opposites: correlatives (e.g., double, half); contraries (e.g., good and bad, black and white); privation and possession (e.g., blindness and sight); affirmation and negation (e.g., "He is sitting," "He is not sitting."). The first three types of opposition, which we have briefly mentioned, pertain to real entities, while the last pertains to propositions. Even in this last case, we may say that the realities underlying the statements are in opposition. Indeed, our intuition regarding the opposition of affirmative and negative statements comes from a conviction that the underlying realities described by such statements are mutually exclusive. The opposition of affirmative and negative statements is a consequence of the other three types of opposition, insofar as they are manifested in a pair of statements. This basis for the principle of non-contradiction is quite different from that of a formal logician, for whom non-contradiction is just an arbitrary axiom among many possible choices. This difference of approach highlights the distinction between philosophy and mathematical or formal logic.

Correlative opposites are defined in relation to each other, so they have an ontological, even conceptual, interdependence. There could be no such thing as "double" unless there is also such a thing as "half" with respect to the same subject. Indeed, in ancient Greek, "double" was understood to consist of two "halves," while "half" was half of a "double." If we use the conventions of modern English and Romance languages, a "double" would be four times a half, yet the interdependence of "doubling" and "halving" relations remain. Correlative opposites denote inverse or reciprocal relations, which we discussed in our overview of relations. We observed then that virtually any asymmetric two-predicate relation, or "relative," when given properly (with respect to essential attributes), admits of reciprocation. The only exceptions we discerned were relations defining potential knowledge and perception, which have no reciprocal.

Contrary opposites are more absolutely opposed than correlatives, since they are not defined in relation to each other. Entities that are essentially contrary are mutually exclusive; to the degree one is present, the other is absent. There is nothing black about white, and nothing white about black; they are altogether distinct qualities. Nonetheless, contraries, in order to be in opposition, must have some common property or genus. Black and white can be opposites only because they are colors, and they are considered qualitative opposites because they are in some sense maximally unlike, insofar as colors are considered. In geometry, two points on a circle are diametrically opposite, only if they lie on the same diameter, but on opposing ends, so they are maximally distant for points on a circle. In other words, contrary entities must be in opposition with respect to some accident (brightness, ends of a diameter), yet hold some other feature in common (being a color, lying on the same diameter) to form the basis of comparison. Contrary opposites may be qualities or relatives, but when they are relatives they are not defined by their opposites, as are correlatives. Substances can be contraries only incidentally, insofar as they manifest contrary qualities or relatives.

The only way a pair of opposites could have nothing in common would be if they were opposed with respect to the totality of their being, as in the opposition between the presence and absence of an entity. This radical form of opposition may be characterized as "presence" or "absence." This may be directly predicable not only of accidents, but of substance itself. We might see this form of opposition as a more perfect contrariety, as these opposites are absolutely opposed (an "absent man" is not ontologically dependent on a "present man" or vice versa), yet they hold absolutely nothing in common, as every aspect of the present being is negated in its absence.

Presence and absence are directly predicable of ontologically simple entities. The presence or absence of complex entities is determined simply by the presence or absence of the simple entities of which they are composed. If all the simple entities essential to the complex entity are present, then the complex entity is present. If at least one essential simple entity is absent, then the complex entity is absent. Naturally, we specify only essential aspects, as the presence or absence of a man is not determined by a change in his hair color. For those who reject essentialism, it would be necessary to regard every object as sui generis, so that any minor change represents the replacement of one object by another. This view runs into serious metaphysical difficulties when dealing with the problem of motion, but it does not affect our statements regarding presence and absence, save that all simple entities of which a complex entity is composed would be regarded as essential.

Classical discussions of opposites only deal with a particular kind of presence and absence, known as possession and privation. This refers only to accidents that are present or absent in a subject. In order for such accidents to be opposites, they must be predicated of the same kind of substance. Thus "sight" is the opposite of "blindness" only if both are predicated of a common genus, such as animals. We would not say a rock is blind, since "sight" is not predicable of a rock. Such judgments as to whether an absent accident qualifies as a privation depend on whether the possession of the accident is "natural" to the substance in which it is absent, by which we mean only that it is physically possible for the substance to possess such an accident. This requires some knowledge of natural philosophy, without which we cannot determine whether an absence is truly a privation.

Contraries, we have mentioned, are absolute in their mutual opposition, yet some contraries may admit of intermediates. Aristotle asserts that no intermediate is possible between contraries when the subjects of which they are predicated necessarily contain one or the other contrary. For example, "sickness" and "health" can only have living things as subjects, and it is necessary for every living thing to be sick or healthy, but not neither. Similarly, "odd" and "even" can only have integers as subjects, and it is necessary for every integer to be odd or even, but not neither. According to Aristotle, this means that no intermediate is possible between these pairs of contraries. Conversely, where no such necessity obtains, an intermediate is possible. For example, "black" and "white" may have any visible object as their subject, yet there are many visible objects that are neither black nor white. Thus it is possible for there to be an intermediate between black and white. We shall examine these claims critically.

To be intermediate means to be partway in between two extremes or contraries. An intermediate is only conceivable if the two extremes may be considered with respect to a common measure (intensive or extensive) that varies by degree, and admits of a value other than the two extremes. We are justified, then, in restricting our inquiries to contraries that may vary by degree.

An intermediate might be regarded as independent of the two contraries, though dependent on their common measure, or it may be considered a compound of the contraries. In the latter consideration, the contraries are still absolutely opposed, in the sense that one must be absent to the degree that the other is present. This is different from the mutual ontological dependence of correlatives, for the presence of a correlative depends on the presence of its opposite, while the presence of a contrary depends on the absence of its opposite, and vice versa. Both ways of regarding intermediates require variation by degree, since the concept of measure requires degree, and, with regard to the second approach, contraries would not be able to coexist in the same subject in reduced degrees, while the perfect manifestation of a contrary excludes the presence of its opposite.

Given that a pair of contraries might admit of variation by degree, or at least be subject to a common measure that admits of degree, there remains a further condition for the existence of an intermediate. There cannot be an intermediate if all possible subjects of these contraries must be the subject of either one or the other contrary, not neither. We may state this formally as follows:

Premise (1): A and B are contraries of each other.
Premise (2): Anything of which A or B is predicable must be the subject of either A or B.

Thesis I: If (1) and (2) are true, then there is no intermediate between A and B.
Thesis II: If (1) is true but (2) is false, then it is possible for there to be an intermediate between A and B.

We may borrow Aristotle's examples of cases where both premises (1) and (2) are true: the contraries "odd" and "even," "sick" and "healthy." "Odd" and "even" are only predicable of integers, and all integers must be either odd or even, not neither. Similarly, "sick" and "healthy" are only predicable of living things, and it is impossible for a living thing to be neither healthy nor sick.

"Odd" and "even" are defined in a way that admit of no gradation. "Odd" means to divisible by one (i.e., an integer) yet not divisible by two, while "even" means to be divisible by two. Since all even and odd numbers are necessarily divisible by one, or integers, the distinction between "odd" and "even" boils down to whether or not an integer is divisible by two. In other words, they are distinguished by an affirmation ("Integer X is divisible by two.") and its negation ("Integer X is not divisible by two.") which admits of nothing in between. This is a simple dichotomy with an excluded middle, so there can be no integer that is an intermediate between "odd" or "even." We will later consider the tendentious possibility that some non-integer might be an intermediate between these contraries.

"Healthy" and "sick," unlike odd and even, admit of variation by degree. If they are to be defined univocally, we would consider an organism "healthy" if it is at or above some threshold of bodily soundness, while regarding it as "sick" if it is below the same threshold. Like odd and even, "healthy" and "sick" span all possible subjects and are defined with respect to an affirmation ("Organism X is at or above the threshold defining health.") and its negation ("Organism X is below the threshold defining health."), once again admitting of no intermediate, since the excluded middle is built into the concept of negation. In set theoretic terms, the set of healthy organisms is necessarily the complement of the set of sick organisms. If there were to be any intermediate between "healthy" and "sick," it would not be predicable of any organism.

The only way remaining for there to be an intermediate when premises (1) and (2) are true would be for the intermediate of contraries A and B to be predicable of a subject of which neither A nor B is predicable. In our examples of choice, this would mean some intermediate "odd-even" is predicable of a non-integer, or some intermediate "healthy-sick" is predicable of non-living things. We shall now determine whether these hypothetical entities could be true intermediates.

An intermediate might be construed as a compound of varying degrees of two contraries, or at least as sharing a common measure with the two contraries. In the examples we have discussed, it is impossible for an intermediate to be a compound of the contraries if its subject is not predicable of either contrary. Anything that has any degree of "oddness" or "evenness" must be an integer, so the only possible subjects of "odd-even" are integers, which we have already eliminated. Similarly, all degrees of "sickness" and "health" are predicable only of living things, so the intermediate "healthy-sick" could not be a compound of degrees of these contraries if it were predicated of non-living things.

There remains, however, the possibility of defining an intermediate by introducing an arbitrary common measure. To be whimsical, I could define the measure "pleasingness" and assign values of 1, 2, and 3 to "odd," "green," and "even," respectively, making green the intermediate between odd and even with respect to "pleasingness." We nonetheless rightly shrink from regarding "green" as an intermediate, since it is predicable of none of the subjects of "odd" or "even". Thus, the truer, less arbitrary, type of intermediate is not merely an entity sharing a common measure with two contraries, but also is capable of inhering in the same subjects as these.

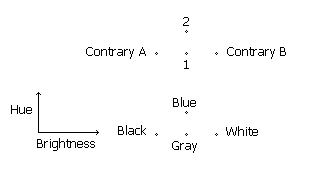
A true intermediate is a compound of varying degrees of two contraries. The variation of degree is critical, for it is not possible for two contraries to be similarly predicated of the same subject, so as one increases in degree, the other must decrease. The intermediate of two contraries A or B is properly neither A nor B, though it has similarities to each. "To be gray" does not mean "to be black" and "to be white" at once; a gray object is neither black nor white, for a black object absorbs all light and a white object reflects all light, while a gray object neither absorbs all light nor reflects all light. A gray object absorbs some light and reflects some light, so it has some kinship to both black and white, though it is neither one nor the other. Gray, indeed, may be considered a compound of black and white, not because it is either of these colors, but because it has differentia similar to those of black and white, differing only in degree.

If Premise (2) above is true, namely that all things of which contraries A and B are (conceivably) predicable must (necessarily) be subjects of either A or B, then it follows that nothing of which A or B are predicable can be the subject of any intermediate. This is because being an intermediate of A and B is incompatible with "being A" or "being B" (as a subject of A or B must be), though the intermediate might be a compound in the sense described above. Aristotle's criterion for the non-existence of an intermediate does hold, but only if we require that intermediates be predicable of the same kinds of subjects as their associated contraries.

Contraries that do admit of intermediates are not related to each other by means of simple affirmation or negation. White is not simply the negation of black; blue, for example, is also not black. The possibility of at least a third distinct predication in the same kind of subject as the contraries is the Aristotelian criterion for the possible presence of an intermediate. We see that this is equivalent to requiring simply that one contrary is not the negation of the other. In the case of black and white, the contraries are opposed by maximum and minimum degrees of some property, be it brightness, light absorption, or light reflection. What makes these properties definitely more than mere formal measures is the fact that they can be exemplified only in the same kinds of subjects as the contraries, which are presumed to be real. Only those subjects that have degrees of "black" or "white" can exemplify brightness, light absorption, or light reflection. Arbitrary formal measures such as the above-mentioned "pleasingness" can have subjects other than those of the real contraries under discussion, so we have no guarantee that these other subjects are true intermediates.

An accident is more truly an intermediate when it is a pure compound of the contraries, not admixed with other features. We can express this geometrically, by considering a point (1) between two extremes along the same line, or another point (2) that is in some sense "between" the two extremes, though not directly. The first point represents an intermediate that is a pure compound of two contraries, such as "gray" with respect to black and white, while the second point corresponds to an impure compound such as "blue with 50% brightness," which has the requisite intermediate measure of brightness between black and white, yet also has the dimension of hue, so it is not a simple intermediate.

Here we are considering colors as perceptibles, not in terms of photonics. This is a real distinction, as evidenced by the fact that although the electromagnetic spectrum rises linearly from red to blue, then violet, the perceptible color spectrum is "circular," in that violet is an intermediate of red and blue. Thus red and violet are contraries with regard to their positions on the visible light spectrum, with blue being an intermediate, but violet is an intermediate of red and blue with regard to hue. Red and blue are not contraries in the latter consideration, showing that an intermediate can exist even when there are no contraries, as in the circular spectrum of hue.

One final aspect of contraries to consider is the categories of which they may be predicated. Since we are considering contraries only with respect to ontology, ignoring purely artificial or formal contraries, we may only use substances and accidents as subjects or predicates of contraries. The predicative relationships of the categories, expounded over the course of this essay, are as follows.

A substance can admit of quality, quantity, place, relation, or time.
A quality can admit of quantity, relation, or time.
A quantity can admit of place or relation.
A relation can admit of time.

Since quantity, place, and time have no contraries (additive inverses and the like are correlative opposites), only several types of predication remain applicable to contraries.

A substance admits of contrary qualities and relations.
A quality admits of contrary relations.
A quantity admits of contrary relations.

From this summary of possible contraries among the categories, we find four categorically distinct types: contrary qualities predicated of substance, contrary relations predicated of substance, contrary relations predicated of quality, and contrary relations predicated of quantity.

Recalling Plato, a thing cannot admit contraries at the same time and in the same respect and in relation to the same thing. Only substances, qualities and accidents can admit of contraries, which are relations or qualities, the latter being predicable only of substance. A pair of contraries have the same genus, so contrary qualities could not inhere in the same substance unless they differed in time, respect (which includes quantity and degree), or relation. Similarly, contrary relations cannot be predicated of the same subjects unless they differ in time. A thing may be large and small at the same time only if it is considered with respect to different things. ("Large" and "small" are relative contraries, not correlatives, since one is not defined in terms of the other.)

Affirmation and Negation

Affirmation and negation are not merely a type of opposition, but the most elemental form of logical analysis of entities in the categories. Affirmation and negation pertain to statements, so they can have truth or falsehood, unlike other sorts of opposites. Indeed, the very concepts of affirmation and negation is intimately bound to those of truth and falsehood. An affirmative statement and its negation are related to each other as opposites, so that to the extent that one statement is true, the other is false. We have seen that some contraries may continuously vary of degree and admit of intermediates. Could there not also be degrees of truth and falsehood, whereby an intermediate between an affirmation and its negation might exist?

A negation is defined as a logical complement of its corresponding affirmation, so that the two statements span all possible truths regarding a matter: either the affirmation is true and the negation is false, or the negation is true and the affirmation is false. This binary truth system is sometimes referred to as the "excluded middle," as it seems to arbitrarily eliminate the possibility of intermediates. In fact, we might more properly call this definition of negation the "included middle," since any putative intermediate statements are contained in the negation. To take a concrete example:

Affirmation: The night sky is black.
Contrary Affirmation: The night sky is white.
Negation: The night sky is not black.

It would be a mistake to take the second statement as the negation of the first, though they differ only by contrary predicates ("black" and "white"). This is because there are many other logically possible colors for the night sky, so the statements are not logical complements. The third statement, by contrast, is a true negation of the first, since it encompasses all the "intermediate" possibilities: "The night sky is gray," "The night sky is blue," etcetera. Another way of expressing this distinction is to say that the third statement is the most generalized negation of the first (with respect to the predicate "is black"), while the second statement is only one particularized negation of the affirmation. The generalized negation is what logicians simply call the "negation," as it contains the essence of the negation or denial of the affirmative statement. What makes "The night sky is white," a particular negation of "The night sky is black," is not whiteness per se, nor the fact that white is the contrary of black, but simply the fact that white is not black. Thus "not black" is essential to the negation. This word "not" (and its associated logical symbols) conceptually contains all possibilities other than those contained in the affirmation. When the negated predicate corresponds to an ontologically simple category, "not" signifies the absence of the named entity, while the corresponding affirmation signifies its presence. Thus, at the simplest level, affirmative and negative statements correspond to the presence or absence of entities.

A basic problem of any logical theory is how to handle statements where the referent does not exist. For example, consider the statements:

Robin Hood is healthy.
Robin Hood is not healthy.

If Robin Hood does not exist, how are we to regard the truth values of these statements? Our answer to this question hinges upon whether we interpret these statements to implicitly include the affirmation "Robin Hood exists." If they do include this affirmation, following Aristotelian convention, then both statements are certainly false. If they do not include this affirmation, as Plato and some modern logicians have held, then we cannot ascribe any truth value to these statements, since we do not know what is being affirmed. Some would say that the second statement, "Robin Hood is not healthy," would be true if Robin Hood does not exist. By that reasoning, "Robin Hood is not sick," would also be true, yet "not sick" simply means "healthy," so "Robin Hood is healthy" would also be true! This absurdity might be avoided by denying that "not sick" means "healthy," but includes the possibility of the subject's non-existence. The fact that the "included middle" belongs with the negation implies that the negation will always be true when a referent is non-existent, while the corresponding affirmation will be false. Either approach to interpreting these statements is valid, as long as we are clear on precisely what we mean by "not" or its corresponding symbol.

The critical issue for resolving the truth value of a negation is to understand what is the affirmation that is being denied. The ambiguity of common language can be aided by the use of logical notation, parenthetically identifying the formula that is negated. Let us begin with the statement, "Robin Hood is healthy," using the Aristotelian interpretation that this entails the affirmation that Robin Hood exists. There are two different ways we can apply negation to this statement.

~(Robin Hood is healthy.)
Robin Hood is ~(healthy).

The first statement is true and the second statement is false, since only the first statement includes the non-existent subject Robin Hood in the negation. If we used a Platonist interpretation of "Robin Hood is healthy," then both negative statements would be true, which involves no contradiction. Note that in both interpretations, the first statement is true while the affirmative is false. Thus a full negation of the entire statement is most truly the negative of the affirmative, and is independent of how we interpret non-existent referents. When we affirm X, we are saying, "It is true that X," so the proper negation of a statement X ought to be of the form ~(X), rather than negate only a predicate or formula within X.

Certain caveats apply to the opposition of affirmation and negation, similar to those that Plato identified for contraries. An affirmation and negation are opposed only when the realities they assert or deny are considered at the same time in the same respect in the same subject. It may seem strange that this triple condition should be built into something as elemental as the contrast between truth and falsehood, but we may see this is so from the following examples.

Socrates is alive.
Socrates is not alive.

These are mutually opposing statements only if referring to the same time. The statements need not be spoken at the same time, but only be understood to refer to the same time.

Hercules is strong (for a man).
Hercules is weak (for a god).

The parenthetic phrases provide context for the statements, "Hercules is strong," and "Hercules is weak," which, on their face, appear to be mutually contradictory. No contradiction exists, however, if the relative qualities "strong" and "weak" are referring to different bases of comparison. Thus the statements are not affirming/denying the same thing, so they are not in contradiction.

I am strong.
I am weak.

Here the predicates "strong" and "weak" might be assumed to have the same context, yet there would still be no mutual contradiction if the "I" in each statement did not refer to the same person. Thus for statements to be opposed as affirmation and negation, it is necessary that every element, including the subject, should have the same referent.

Predication

Throughout our discussion, we have repeatedly referred to entities in the ontological categories as being "predicated" of other entities, though in the first part we clarified that, properly speaking, the name of an entity may be predicated of other entities. This holds when the essence of the predicated entity pertains to the being of its subject. In our discussion of contraries, we summarized the possible predicate relationships across ontological categories, which we review below.

A substance can admit of quality, quantity, place, relation, or time.
A quality can admit of quantity, relation, or time.
A quantity can admit of place or relation.
A relation can admit of time.

We may invert these statements to yield statements about predicability.

Quality is predicable of substance (or other qualities).
Quantity is predicable of quality or substance (or other quantities).
Place is predicable of quantity or substance.
Relation is predicable of quantity, quality, or substance (or other relations, in an improper sense).
Time is predicable of quality, relation, or substance.

I parenthetically note that qualities, quantities, and relations are predicable of entities in their own category. We can easily think of examples for quality and quantity, such as "the brightness of a hue," or "seven sevens." Relations are not strictly predicable of other relations, but rather their predicates or arguments may be the arguments of a higher-order relation. For example, the relation "square magnitude," or x² + y², may be regarded as a composition of the "addition" and "squaring" relations, so that "square magnitude" might be said to relate "addition" and "squaring". In reality, no relation between "addition" and "squaring" themselves is generated, but rather their arguments x and y are related in a more complex way. Though it is conceptually useful to compose relations of other relations, we should not mistake this formal composition for ontological predication.

Place and time are not predicable of entities in the same category; indeed, place and time are not the subjects of any accident. There is no "place of a place" because place is simply and directly predicable of quantity or substance as a primary accident. Place is the subject of no accident, having no quality or quantity, as space is ineffably simple. Time, similarly, admits of no accident, and there is no "time of a time." Space and time are the background against which other accidents are manifested, and are much too ethereal to admit of modification. Modern physics gives qualitative and quantitative descriptions of "space" and "time" or "spacetime" as though they were property-bearing substances, yet this is not the same as metaphysical space and time, as we discussed previously. A quantity may have a place, and we may speak of relations between quantities that have place; such relations are not accidents of place, but of the quantities of which place is predicated. Time, in turn, may be treated as an extensive quantity, only by relating it to quantities of spatial displacement.

The remaining predicative relationships may be established by expounding the original set of four statements. The first statement simply expresses the relationship between substance and accidents, which we discussed at length in Part I. There we described individual accidents as "inhering" in a primary substance, and universal accidents as "differentiating" secondary substances. Inherence and differentiation are modes by which accidents may be predicated of substances. These modes of predication, however, do not collapse the ontological categories, for when we say, "The leaf is green," we do not mean that "leaf" and "green" are of the same ontological category, for this is not a statement of identity. The accident "green" is something that modifies the being of the substance "leaf," but "green" is not thereby a substance, nor any part of a substance. In trope theory, the distinction between substance and accident is collapsed because the object is viewed as nothing more than a composite of accidents. In this view, the predication of accidents in a substance is interpreted as a part-to-whole relation or an element-to-set relation. We have briefly discussed how set theory is an inadequate model for ontology, since it does not grasp the relations of the ontological square. It ignores the problem of universals rather than solving it, since secondary substances are misconstrued as mere sets of objects. Somewhat closer to the concept of a universal is the notion of a "class," but unfortunately, this is narrowly construed in terms of computer programming syntax, where a class is just a label assigned to a set of differentiae. Once again, the (universal) accidents are considered mere elements of a set (the class, or pseudo-species), and mathematical logic fails to grasp the predicative relationship between substance and accident. This relationship of being "in a subject" was discussed at length in the first part.

Quantity, relation and time may be predicated of a quality, each in a distinct way. Quantity tells us the degree to which a quality is manifested. Specifying the time that a quality is manifested does not modify the essence of that quality, but rather restricts the relationship of that quality to its subject. A relation can compare a quality to other qualities, or to other degrees, or to other times.

Quantity, when it modifies substance, may admit of place. Under any circumstances, it admits of relation, which may be expressed mathematically or geometrically. Specification of place need not modify the essence of the substance quantified, and it certainly does not modify the quantity itself. Place is an additional datum added to quantity, enabling relative comparisons to other quantities. It is arguably not properly predicated of quantity itself, but of the substance quantified.

Relations need not inhere in a particular subject, but may be predicated of multiple subjects without inhering in any. A simple example of this is the distance relation. The distance |AB| between points A and B is predicable of these two points, upon which it depends for its being, but this predication is very different from that of inhering in a substance, for the distance cannot be "said of" either point in the manner we discussed in Part I. This important distinction is completely lost in formal modern logic, which regards the predicate relations Color(X) (the color of X) and Distance(A,B) (the distance between A and B) as differing only in the number of predicates, when in fact the very nature of predication can be fundamentally different. Color(X) can be "said of" X, while Distance(A,B) may not be said of A or B. When we say "X is green," we are making a much more powerful existential identification between X and "green" than when we say, "The distance between A and B is two miles." "Two miles" is not in any way inherent in A or B. It is not a mere matter of grammatical convention that we do not say "A is two miles," "B is two miles," or "A and B are two miles" in any sense. We do not say any of these things because we mean something different when we predicate distance of two points than when we predicate something inherent, such as "Blue is the color of the sky." To parse the latter sentence simply as a two-place predicate relation, Color(blue, sky), loses valuable information about the existential relationship between blue and the sky.

None of the other categories are predicable of relation, save time. This may seem strange, since the arguments or variables of each relation are called predicates, yet they are not ontologically predicated of the relation itself, but of the subject of that relation. For example, when we say, "Adam is the father of Seth," or formally, Fatherhood(Adam, Seth), neither Adam nor Seth in any way modify the being of the fatherhood relation, though Seth may modify Adam by being in relation to him. We would not say "Adam is fatherhood," or that "fatherhood of Seth" is a type of fatherhood; rather the predicates Adam and Seth taken together instantiate the universal relation, "fatherhood." This is even more obvious for mathematical relations. The addition relation, with quantitative predicates x, y, may be expressed as "The sum of x and y," or Sum(x,y), yet this does not mean that quantity is predicable of the relation itself. If we increase the quantitative magnitude of x and y, that would not make Sum(x,y) any more of a sum. 1 + 1 = 2 is a sum as much as 100 + 100 = 200 is a sum. With qualitative predicates, as in, "The night is dark and stormy," the qualities are predicated of the subject, not of the relation. Formal predicate logic, while a useful calculus, does not abolish the need for real ontological subjects of which accidents may be predicated. This can be clearly apprehended when we recognize that the "predicates" of such logic are really arguments that instantiate the universal relation, but are not ontologically predicable of the relation itself.

Time alone is ontologically predicable of relations. A relation may be modified by whether it is occurrently instantiated, or has been in the past, or will be. Alternatively, a relation may have its time-dependent component built into it. For example, the static distance relation D(x,y) may be modified by time, as objects x and y move closer together or further apart. Thus, the being of D(x,y) would vary with respect to time. We could instead formulate a time-dependent distance relation D(x,y,t); in this case, the relation D is not extrinsically modified by time, but rather time-dependent variation is built into the definition of the relation, which takes a time variable as an extra predicate. The time variable is an extensive quantity related to quantities of spatial displacement, not time itself.

Value

Entities may vary according to value, by which I mean the normative attributes "good," "bad," and their various gradations. In mathematics, the term "value" is used in a different sense, meaning quantity, while in formal logic and computer science, the value of an argument or predicate is the particular name or symbol representing some entity in a relation or declaration. We are not using value in either of these senses, and it would be a mistake to conflate the valuation of good and bad with value in a quantitative or syntactic sense. Neither mathematics nor syntactic logic are especially useful for the valuation of good and bad, which occurs at a very basic ontological level.

It may seem strange that "good" and "bad" should belong to a discussion of ontology, but for philosophers from antiquity through the early modern era, the Good has been an essential philosophical concept, as basic as Truth or Reality. Indeed, for Socrates, the Stoics and others, it has been the principal motivation of the philosophical enterprise. Man loves wisdom because wisdom enables him to become a better person by discerning the Good. In our age of moral relativism, we tend to psychologize the good, making it a feature of the human mind rather than of objective reality. With a utilitarian ethic, one defines the good purely in terms of what a person desires. Yet if the Good is nothing more than what we desire, then philosophy cannot help us find the Good, since even the ignorant are capable of desire, and there is no basis for judging the object of the philosopher's desire as more "good" than that of a rogue or a brute beast. This would mean knowledge is not a guide for action, so intellect or understanding would be useless. In fact, most utilitarians do smuggle into their system a notion of the Good, being the survival of the organism or its physical or emotional pleasure. The intellect is useful insofar as it helps the organism to survive or experience pleasure. We should emphasize that, without a concept of the Good, there is no basis for requiring that an organism ought to survive or seek pleasure. The Good is essential to any complete ontology that does not regard philosophy or wisdom as being utterly in vain.

The Good reflects what an entity ought to become or ought to do. The Good is thus in some sense the realization of an entity's being or the actualization of its potential. This teleological aspect of being is captured in the Aristotelian term entelechia, which is both the actualization and the end of an entity, the "becoming-at-an-end." It is beyond the scope of our discussion to account for why potentiality and actuality (dunamis and entelechia) are necessary to solve the problem of change or motion. Suffice it to note that the existence of the Good presumes a metaphysical teleology of which it is the object. Thus, if there is any Good at all, there must be a metaphysical good.

Scholastic philosophy distinguishes three levels of good: metaphysical good (entelechia), moral or ethical good, and physical good (pleasure, comfort, structural integrity or health). In many modern discussions of ethics, the three types of good are collapsed or confused. Most commonly, the metaphysical good is ignored, leaving no grounding for the ethical good save arbitrary desire, and often making little distinction between ethical and physical good. This last error pervades modern theology, where the "problem of evil" is miscast, making it effectively a "problem of suffering," as if the essence of moral evil lay in the suffering that is but one of its possible results. We will take care to distinguish the three notions of good and bad, examining each of these in turn.

Metaphysical good is the realization of the metaphysical end or telos of an entity. The extent to which an entity actualizes its telos is the extent to which it is metaphysically good, while insofar as it falls short, it is deficient or "bad." Only when the telos is fully realized can something be regarded as metaphysically good, simply and absolutely. If an entity is subject to extrinsic influence that directs it away from its natural end, it is "bad" in a stronger sense than that of deficiency, for it is now inclined against its nature (contra phusis). Although metaphysical good and bad do not correspond to our familiar moral notions of good and evil, the metaphysical concepts do provide a background for the moral notions. In calling the natural telos of an object "good," Aristotelians have not projected human morality onto inanimate nature, but rather have identified an aspect of nature (goal-directedness) that might serve as a metaphysical basis for human morality.

Metaphysical good and bad can be predicated of any category of entity. Value is not a separate category, but an expression of the degree of actualization. Actualization, as the fullness of being, transcends the categories, and so good and bad transcend the categories. This means good and bad are not in a genus. We may inquire whether good or bad itself may constitute a genus: is there a genus of "good things"? If being and goodness are equivalent, as St. Thomas Aquinas interpreted Aristotle, then good certainly cannot be a genus. Even without this equivalence, we may note that the actualization of an entity's telos does not necessarily change its essence (on the contrary, it often entails a more perfect realization of its essence), so there could not be a class of "good essences" unequivocally distinguishable from bad essences.

Goodness in the moral sense is applied to intelligent actions or dispositions to act (i.e., desires). There can only be morality where there is understanding (intellect) and a will acting according to that understanding. Thus the actions and dispositions of brute beasts and inanimate objects have no moral value. For intellectual beings, the moral good consists in what one ought to will; that is, it concerns the proper exercise of the will. The moral good may be thought of as the metaphysical good of intelligent volition. The exact content of moral good is the subject for a system of ethics.

Lastly, the concept of physical good may be applied to entities lacking volition. Animals sufficiently sentient to experience physical or emotional pleasure may be said to find their physical good insofar as they achieve such pleasure. Other lifeforms may have the physical good of health, and inanimate objects may have the physical good of structural integrity. All of these are particular manifestations of metaphysical good. Pleasure is the perfection or goal of appetition, while health is the perfection or goal of vital processes, and structural integrity means the essence of an object is most perfectly realized.

Utilitarianism, often invoking pseudo-Darwinian rationalization, attempts to reduce all good to physical goods such as pleasure. This makes for a crude ethic that poorly accounts for altruistic virtues, as sociobiologists try to reduce these to some underlying selfishness or survival mechanism. Indeed, none of human morality is reducible to physical good, since the intellect and will are not reducible to mere appetition. The contrast between human ethics and physiological desires should be evident from the fact that countless cultural upheavals have occurred in recorded history, during which time human physiology has been nearly unchanged, making it implausible that our ethical behavior should be a matter of biological inheritance. The question of biological inheritance is further rendered moot from the apparent fact that humans adhere to moral principles consciously, not instinctively, and have often freely rejected the principles of their immediate ancestors. Lastly, physiology does not dictate behavior or function, even among lower animals. Biologists do not pretend to deduce the behavior of giant squid without observing a live specimen, so it is disingenuous to pretend that there is any scientific weight behind speculation on the behavior of australopithecines based on mere fossil remains.

In our discussion of qualities, we observed that good and evil are predicated of habits and dispositions, which may belong to intellectual substances, animals, and simple bodies. Metaphysical and physical good may apply to all of these while moral good applies only to the first. Physical good varies by subject, being merely health or pleasure in lower animals, and structural integrity in inanimate objects (though perhaps not for simple bodies, if these are structureless).

Good and bad might be called contraries, not that good and bad are entities, but because good and bad entities are necessarily contrary in some regard. Good and bad qualities are contrary qualities; good and bad relations are contrary relations. Good and bad substances are contrary substances improperly speaking, insofar as they manifest contrary qualities or relations. No substance is properly bad, since substance is predicated simply of being, and as such, is good, the more so the more perfect its being. Thus substance may have degrees of goodness, but only its privation is bad.

The contrary of a good thing is necessarily bad, as it is without the presence of that good and therefore defective. Yet the contrary of a bad thing might also be bad, as in the case of excess and deficiency, where the good is some "golden mean." This principle has limited application, however, and we usually find the contrary of a bad thing to be good insofar as it is contrary to what we find defective. Accidental evils that inhere in that contrary good are of no relevance. For example, if lechery is evil, then the chaste man is good insofar as he is chaste, but it is no argument against the goodness of chastity that the chaste man happens to be a thief. We are speaking of good and evil, of course, in the metaphysical sense, of which the moral and physical senses are but special cases.

Priority

Entities can be arranged in a sequential, direction-dependent order, so that we may regard them as prior or posterior to each other. There are several different senses of priority, including: temporal, existential, scientific, semantic, and by value (goodness), this last being the least proper. For each of these kinds of priority, we define "simultaneous" as being neither prior nor posterior. All senses of priority constitute an asymmetric order, which may be conceived linearly or hierarchically in particular instances.

In the temporal order, prior and posterior simply mean "before" and "after." There need not be a universal measure of time, and relativity insists there is not, but within each local temporal sequence or world-line, there must be an order of successive instants. Each instant in time is succeeded by another, and the position of an instant in this temporal order has implications for causal priority. An effect cannot occur before its cause in time, though they might be simultaneous, but a cause can certainly occur before its effect. Since the order of time affects other forms of priority, it is logical for us to regard instants further in the past as being "prior" to more recent instants. Even if we did not consider the relationship between the temporal and causal orders, we still would be inclined to regard the past as prior, since the order in which we experience instants goes from past to future, with each experience being added to those of the past. The instants that are earlier in the order of time are added to our experience first, followed by those that are later. Indeed, our concepts of first and last, prior and posterior, are temporal in origin, following the sequential nature of our psychological life, as parameterized by time.

Simultaneity, which we will generalize to all forms of priority, is proper to time in its primary meaning, and refers to events that are neither prior nor posterior to each other, yet exist within the same temporal order. Although relativity has undermined the possibility of universal temporal simultaneity, it has not abolished the need for local temporal orders that are interwoven with each other. Since temporal priority has long been bound up with causal and even existential priority, we might fear that relativity undermines the causal and existential unity of the universe. This is not the case, for while the temporal, causal and existential orders are interdependent, they are not identical.

The existential order of priority concerns the dependence of entities on each other for existence. An object A that cannot possibly exist without object B also existing at some point may be said to be existentially dependent upon or posterior to B. This order of existential dependence may be a matter of logical, metaphysical, or physical necessity. As an example of each: area cannot exist without two dimensions; an effect cannot exist without a cause; and a chicken's egg cannot exist without a chicken. In each of these orders of dependence, we may define a sense of priority if the dependence is non-reciprocating. We regard the dependent entity as posterior by analogy with the temporal order, since a dependent entity A may be posterior to (or simultaneous with) B in the order of time, but it may not be prior to the original existence of object B. Existential priority is logically constrained by the temporal order on a priori grounds, since by definition, a dependent object cannot exist unless that upon which it is dependent exists. The existentially prior object might even have perished before the dependent object came into existence, if the dependence is indirect, as a grandfather generates a grandson.

With categorically simple entities, logical necessity is non-reciprocating when one entity is more specific or particular than the other. For man, a rational animal, to exist, it is necessary that "animal" should exist; this is true both in the universal and particular orders. The species "man" cannot exist without the genus "animal," and an individual man cannot exist unless an individual animal exists, but the converse is not true in either case. In a similar fashion, accidents are existentially dependent on substance. Entities that are prior and posterior in the order of logical necessity can nonetheless be simultaneous in the temporal order, as in the cases we have described. When logical necessity is reciprocating, as in our example of the existence of area and of two dimensions, we may regard the two entities as simultaneous in the order of existential priority, considered logically.

Causality is but a particular type of existential order, arising from the metaphysical thesis that every effect must have a cause as its source. We will not justify this thesis here, but simply expound the relationship between causal priority and the orders of priority already discussed. Clearly, if the metaphysical thesis is correct, a cause is existentially prior to its effect as a matter of metaphysical necessity. The cause must be prior to or simultaneous with its effect in the temporal order.

This necessity has led some philosophers, following Hume, to suppose that the causal order is nothing more than the temporal order. Indeed, in deterministic systems, where a certain effect invariably follows from a given cause, we might equally say, as a matter of logical necessity (coupled with the metaphysical assumption of causality and a posteriori knowledge of physics), that the cause cannot exist without the effect eventually coming into existence. It would seem that the cause's claim to priority in such cases is solely temporal, not existential.

We may distinguish causal priority from temporal priority by considering an example where these are distinct. An entity may invariably precede another in the temporal order without being its cause. For example, if an animal gives birth to twin offspring, the parent may be regarded as an indirect cause of each twin's development into adulthood, yet the childhood development of one twin would not be considered the cause of the other's maturation, even though it necessarily precedes the latter in the order of time. We do not regard it as a cause because, hypothetically, if one twin died in infancy, the maturation of the other would not be effected. We restrict causality to existential necessity, not mere temporal priority. Hume understood necessity purely as mathematical necessity, or a probability value of 1, as do many modern successors. Yet we understand necessity differently, as the imparting of being from one entity to another. Indeed, this is what we mean when we say A causes B: A gives being to B. This a stronger statement than mathematical necessity, for even if all animals were immortal we would not consider one youth to be the cause of its sibling's adulthood, even though it was invariably prior in the order of time.

Causal priority is different from logical necessity, for, in some deterministic systems, the effect implies the existence of the cause no less than the cause implies the effect. For example, supposing that only chickens can generate chicken eggs, the existence of an egg (coupled with the requirement that every effect must have a cause) would logically imply the existence of a chicken at some prior point in time. In Newtonian mechanics, prior and posterior actions in the order of causality can be derived from one another with equal necessity, so the effect logically implies the cause and the cause implies the effect. We cannot regard the cause as prior to the effect purely on the grounds of logical necessity, but must also consider the fact that the being of the effect is derivative of the being of the cause. This metaphysical consideration may help us distinguish in priority entities whose existence or possibility are logically equivalent, such as space and bodies, though we would need additional metaphysical theses to make these judgments.

We may also distinguish a sense of priority in the order of science or knowledge, by which we refer not to actual physical or metaphysical causality, but to our order of understanding. Some things cannot be made intelligible unless some prior concept or judgment is first considered. This order of priority would seem to depend on our psychological makeup, and the temporal sequence of concepts and judgments that is necessary for our understanding. It is the work of epistemology, philosophical psychology and metaphysics to show that the order of science depends not merely on human psychology, but on the nature of intelligibility as predicated of known objects.

We will take a Scholastic example to illustrate the order of science as distinct from the existential orders (logical, metaphysical, physical). In Thomistic metaphysics, Being, Unity, the True, and the Good are all metaphysically equivalent, and we would call them "simultaneous" in the order of existential dependence, considered metaphysically. Yet we must first conceive of Being in order to arrive at the concept of Unity, for once we recognize that something "is," we see that it "is something," a unity. By virtue of being a certain "something," it is distinguished from other things, and the concept of truth and falsehood, with the principle of contradiction, emerges as we reflect that a thing cannot both be and not be itself. Finally, the will may direct itself to knowing the truth about Being, and this consideration of Being is the Good. Being, Unity, the True, and the Good are in descending order of priority in the order of science, as we can only understand the first before we understand the next. This order is an artifact of discursive thinking, for in fact the four concepts are really reflections on the same primary notion, without adding additional premises. This exposition might be called a priori analytic judgment. With a priori synthetic judgments, where we introduce additional premises along the way to arrive at more complex conclusions, the order from primitive to less primitive ideas is more pronounced. There is no necessary relationship between the scientific order and the existential orders, but this is not a reason to disregard the order of science as "subjective" or "psychological," since this order seems to be independent of culture, following an objective structure of its own, that would be explored in some detail by Kant, and more cogently by Husserl.

The semantic order, or order of speech, is culturally contingent, unlike the order of science. The sequence of speech from beginning to end can vary according to arbitrary rules of grammar, yet these rules are often constrained by a logic of meaning, so that we cannot utterly deny any objectivity to the semantic order. The objectivity of the semantic order is more evident when we view speech on a larger scale, going sentence by sentence rather than word by word. On this level, a certain logic emerges, as we cannot make conclusions unless concepts or premises were established in previous sentences. A more thorough examination of the semantic order would require an exploration of the relationship between language and logic, which we reserve for another essay.

The least proper sense of priority, the order of value, is also the most common. We order things as "better" or "worse" not only in assessment of their metaphysical or moral good, but also with regard to their utility. The value of a thing is defined with respect to some end. While metaphysical, moral, and physical goods admit of some objectivity, utility can be defined relative to any arbitrarily defined objective. Value in the sense of utility can lose its objective status if utility is not directed toward a metaphysical, moral, or physical good. The most common expression of use-value is economic or monetary value. In the order of value, it is not immediately clear if the thing more highly valued ought to be regarded as "prior" or "posterior." Since evil is but a privation of good, there is no question of an entity depending on another entity for its existence. In the order of science, we do not contemplate the lack of something without first considering the thing lacked, so we might thereby be inclined to regard the good as prior to evil. This does not imply existential or temporal priority.

We should note that there is not a single order of value, but many orders, depending on the useful end that is considered. If we restrict consideration to the objective orders of value, we may expect a consistency among them analogous to the interweaving of world-lines that renders temporal priority coherent. We may regard a sick dog as physically worse than a healthy dog, and a sick tree as worse than a healthy tree. Though we might not be able to directly evaluate whether a dog or a tree is more healthy (consider trees and dogs as analogous to different world-lines), we may nonetheless be sure that they will be consistently valued in orders where they intersect, such as their status as living things, since the reality defined by each objective order of goodness coexists in a unified reality.

Change

Action, we have observed, is a highly important type of time-dependent relation that denotes the means by which entities come into being or are changed into other entities. Change (as a noun) is the effect of action, and may be classified according to the various kinds of possible actions: generation, destruction, increase, diminution, alteration, and local motion. The effects of each of these actions is a corresponding change of the same name.

Generative change is the presence of an entity where it once was absent. Its contrary is destruction, which is the absence of an entity once present. Only entities with contingent existences are possible subjects of generation and destruction. A metaphysically necessary being, for which it is impossible not to exist, is not subject to generation or destruction, nor is a metaphysically necessary privation. The effect of generation is the created entity, and the effect of destruction is the privation of the destroyed entity. Substances are most properly the subjects of generation and destruction, as the existence of accidents depends on that of their substantial subjects.

Increase and diminution effect an entity of greater or lesser magnitude. The accidents subject to this change are quantity, quality and relation. Space and time admit of increase and diminution only by improper analogy. What actually increases or shrinks are space or time intervals, which are relations between objects.

Alteration is the substitution of one quality for another, and is arguably prototypical of the entire concept of change, to the extent that alteration and change are synonyms in ordinary speech. Change in the more generalized sense can include the substitution of one quantity for another, or the substitution of an existing essent with a privation or vice versa. Alteration only substitutes quality for quality, so the effect of an alteration is the new quality inhering in a substance. Since qualities depend on substances for existence, alteration presupposes the presence of substance.

A quality is always replaced by another quality in the same genus unless there is some accompanying change in the kind or quantity of substance. For example, if an object shrinks sufficiently in size, it may lose the quality of color. More trivially, if a substance is annihilated or transmuted into another kind of substance, certain qualities or attributes may no longer be applicable at all. Absent any such change, however, a quality may not disappear without being replaced by another quality in its genus. A thing that changes color will still be predicable of color if there is no substantial change, so there must be some other color taking its place.

Alteration need not be confined to such accidental changes, as qualities can be differentia defining species of substance, so that their alteration would constitute an essential change. In such cases, the principal effect of alteration is the new quality, with the change in species being a necessary consequence of the alteration. It would be gratuitous to require that alteration of differentia should entail the annihilation and creation of substance, though we cannot eliminate that possibility a priori at this point.

Local motion has as its effect the new position of an object, either absolutely or relative to other objects. Most modern physicists since Galileo have regarded position as purely relative, making local motion a strictly relative change. As position is an accident, local motion presumes the existence of substance. Local motion can be associated with substantial change, as relations may define essences as do other accidents. The homogeneity of space, combined with the relativity of position, seems to eliminate the possibility of objective substantial change based purely on displacement. In Galilean relativity, the same might be said of velocity, but with Einstein there is at least one absolute velocity, the speed of light in a vacuum, with respect to which others may be defined, perhaps opening the possibility of substantial change linked to change in velocity. Acceleration, whether linear or angular, certainly provides a basis for substantial change, as it is proportionate to force. Local motions that effect substantial change have as their principal effect the new motion (e.g., acceleration), and do not necessarily involve the annihilation and creation of substance, but may merely transmute the substance.

Our discussion of alteration and local motion touched upon the problem of whether substance is annihilated and created during the change of its essential qualities. More generally, the metaphysical problem of change may be expressed as an inquiry into what is destroyed, what is created, and what remains the same. The early Greek attempts to answer this question yielded paradoxical results, until Aristotle introduced his hylomorphic solution. We will reserve discussion of this problem for a metaphysical treatment of change.

Modality

Categorical entities may also be analyzed in terms of their existential modality, defined by the concepts of possible/impossible, existent/non-existent, necessary/contingent. Modality in this sense is not a variation in what an entity is (its essence), but describes in what sense the entity may be said "to be" (its existential status). Existence does not make an essence different from what it is: the essence of an existent elephant is no different from that of a hypothetical elephant. Kant viewed this fact as evidence that there is no such thing as existence as distinct from essence, but Kant was operating in the psychological realm, not ontology. It adds nothing to the concept of an elephant to conceive of it as existing, but it does add to the reality of the elephant if it actually exists. Existence is the actualization of an essence, and modality, in the senses we are considering, describes the existential actuality of an entity.

The simplest modal distinction, upon which the others are built, is that between the existent and the non-existent. Throughout our ontological discussions, we have usually spoken of entities without regard for whether they actually exist or are merely imaginary possibilities, though we have sometimes invoked existent entities as concrete examples. Ontology is concerned only with what is a priori possible, but metaphysics is concerned with what actually is. When dealing with a posteriori reality, we will need to distinguish existent and non-existent entities. We can make this distinction on a hypothetical a priori level, as when we say, "Suppose X exists," and, "Suppose Y does not exist," or in the more common a posteriori assertions, "X exists," and "Y does not exist." In both cases, the logic of such statements is the same, being expressed in the principle of contradiction.

Our discussion of change made clear that it is at least hypothetically possible for substances and accidents to come into and out of existence. Existence is a primitive concept that need not be defined, as it is intelligible to all. While we can intuitively apprehend existence, we only understand its negation formally, and cannot really conceive of non-existence. Thus the antithesis between existence and non-existence depends not only on our intuition of existence, but also on our formal understanding of negation. It would be useless to offer a logical demonstration of these principles, as they in fact underlie all logic as we know it. Instead, we will examine how other existential modalities are related to these primitive concepts.

Not every entity with a coherent description necessarily is capable of existing. For example, we can conceive of an accident abstracted from substance, yet the accident is not capable of actually existing as an individuated trope without substance. We might also conceive of a father whose son is his own father, yet it is not possible for such a man to exist due to the nature of metaphysical time. A knowledge of physics or metaphysics a posteriori might also eliminate certain entities from existing, such as a perpetual motion machine. Entities that are incapable of existence may be called impossible, while those that may exist are possible.

In Aristotle's metaphysics, actually existing entities were not counted among the possible, but only those that might exist. The reason for excluding actual existents from the "possible" was to emphasize the distinction between potentiality and actuality. For Aristotle, potentiality and possibility are equivalent, while the actuality of an essence is its existence.

In modern probability theory, an actuality is expressed by a probability value of 1, while impossibility is zero and possibility is measured by some fraction. The probability of an event X, the actualization of some entity, is calculated by taking the ratio of possible scenarios with X occurring divided the total number of possible scenarios in the condition being considered. Unless there is reason to believe otherwise, we assume that all scenarios are a priori equally probable. Clearly, the measure of probability involves assumptions regarding the a priori likelihood of different scenarios as well as the range of scenarios to be considered. The range is always defined by some condition; even "unconditional" probability assumes at least the axioms of logic, and perhaps some basic metaphysical theses and laws of nature.

The quantification of fractional probability lacks objectivity, since it is contingent upon our choice of condition. The likelihood that a particular man may die in the next ten years may vary greatly depending on how much information we specify about that man. Only probabilities of one and zero are invariant, in the sense that, once specified, they no longer vary with condition. Probability 1 means the entity actually exists, while probability 0 means the entity does not exist, either because it is impossible or because it has been observed not to exist, though it was possible a priori. Probabilities 1 and 0 correspond to existence and non-existence, so they are mutually exclusive. It is the intermediate values, however, that are essential to the concept of possibility.

When we consider a thing as possible, we assert neither its existence nor non-existence, but declare the absence of any obstacle of logic (or metaphysics or physics, depending on condition) preventing its actualization. Further, by articulating at least one scenario whereby it might be actualized, we declare that the power or potential to actualize this entity exists. The relationship between potentiality and possibility requires metaphysical exposition, but for ontological purposes it suffices to define possibility as the absence of absolute logical or ontological barriers to existence.

We may observe that an event with probability 1 certainly has no obstacles to its existence, so it perhaps should be counted among the possible. The only reason for its exclusion would be on metaphysical grounds, namely that the power or potential to actualize the entity has been expended, so the potentiality no longer exists. Whether we exclude or include actual existents among the possible is a matter of terminology, but it is important to be consistent in how we treat events of probability 1. I will follow the Aristotelian convention of distinguishing the actual from the merely possible, not because I wish to incorporate the metaphysics of potentiality, but in order to have a richer ontological vocabulary.

The most misunderstood of the classical existential modalities is the dichotomy of necessary and contingent entities. A common error is to equate necessary entities with probability 1. In fact, to declare something necessary is a much stronger statement than to say it exists with probability 1, for the latter includes all actually existing entities, even those that came into being contingently. Asserting that an entity is necessary is even stronger than the statement that the anterior probability of the event was 1. We can see this distinction from a mathematical example: the anterior probability of randomly selecting an irrational number from among the real numbers is 1, yet it is by no means necessary that a randomly selected real number be irrational, as it would be coherent to select a real number. By "necessary," we mean that it is absolutely inconceivable on a fundamental logical (or metaphysical, or physical) level that the contrary should happen. Probability 1 is a necessary but not sufficient condition for existential necessity.

Contingency, similarly, means more than a probability less than one. A contingent being can exist only if some other thing actually exists, so contingency expresses an existential dependence on another entity. That which is contingent might even exist with probability 1. As contingent, it need only be hypothetically possible for it not to exist. More specifically, this non-existence can occur only if the entity upon which it depends is not actualized.

Modality provides a glimpse of the link between ontology and metaphysics. Before we can explore this connection further, we would have to engage in a discussion of deductive logic and epistemology, which we reserve for another work. Here, we will conclude with a recapitulation of the ontological theses we have articulated.

Continue to Part VII

© 2008 Daniel J. Castellano. All rights reserved. http://www.arcaneknowledge.org